| 基于栅格单元优化的多要素辅助的空间插值方法研究 |
2. 江苏师范大学地理测绘与城乡规划学院,江苏 徐州,221116
2. School of Geography, Geomatics and Planning, Jiangsu Normal University, Xuzhou 221116, China
准确掌握土壤理化特性的空间变异规律是现代化农业管理和气候变化研究的关键[1],空间插值方法正是利用野外采集的离散点数据获取土壤属性空间分布特征及其变异规律的主要手段。受土壤母质、土地利用类型、土壤类型和地貌类型等诸多地学环境要素的影响,土壤属性的空间变异极其显著[2]。对于复杂地貌类型区,现有全局插值模型和单一环境要素辅助的插值模型往往难以较好地对整个研究区进行高精度预测。因此,高精度的土壤属性空间插值方法一直是土壤科学相关领域的重要研究内容[3]。
目前,一些学者结合地学信息对土壤属性进行插值,Triantafilis等[4]将土壤电导率数据作为辅助数据估计土壤盐分含量;Kuriakose等[5]结合坡度、高程、土地利用等数据来预测土壤厚度;Hengl等[6]利用土地利用数据预测克罗利亚土壤厚度;Penížek等[7]通过坡长预测土壤厚度;朱阿兴等[8]通过建立土壤-环境推理模型,基于土壤-环境关系模型的土壤相似度模型和对该模型进行赋值的推理技术模拟土壤图。这些学者通过该方式得到了优于传统全局插值模型的结果,但仅结合单一地学要素对多重环境影响下的土壤属性进行插值显然不够完善[9]。
考虑到土壤属性受研究区多重环境要素的综合影响以及不同插值模型自身的适应性,通过集成学习或其他方式对多个插值模型进行优化组合,可以有效集成其优点,从而获得更为理想的插值结果[10]。有学者基于土壤类型、植被类型等环境要素,利用集成学习算法及多种插值模型权重自适应叠加算法模拟青海湖流域土壤钾含量的分布[9, 10]。其局限性在于没有顾及不同插值模型在不同区域的适应性,而是对不同插值结果根据集成算法自适应叠加,虽然插值精度有一定改善,但其空间分异特征却被削弱。
鉴于此,本文以青海湖流域部分区域为研究区,在对不同环境要素参与插值运算的结果进行优选融合的基础上,探究多地学环境要素综合辅助下的土壤属性空间插值方法的可行性。
1 数据与方法 1.1 研究区概况研究区在地质构造运动和长期外应力的综合作用下形成了包括高山、丘陵、台地、冲积平原等的复杂多样的地形地貌特征。该区有大量农牧业活动,用地类型有草原、草甸、少量耕地、宜农地及沿湖湿地等;植被类型主要有高寒草甸、高寒草原等;土壤类型主要有草甸土、黑钙土、栗钙土、沼泽土、风沙土等。近年来,受自然环境条件和人为不合理社会经济活动的影响,土地沙化、草原退化严重,高寒生态环境遭到破坏。
1.2 数据采集空间插值中采样方法起着重要作用[11]。有学者研究了不同采集密度、模式、分布对青海湖流域钾含量空间插值结果的影响[12]。本文结合土地利用类型、地质类型及土壤类型3种环境条件,采用空间分层采样方式进行采样,全区共设置110个采样点。
1.3 实验方法不同的插值方法都有其适应的插值区域[13],鉴于文献[12]已经论证了普通克里金(ordinary Kriging,OK)插值方法适用于青海湖流域土壤钾含量的空间插值,本文使用OK插值方法来完成单一地学要素辅助的土壤钾含量空间插值。其流程图见图 1。
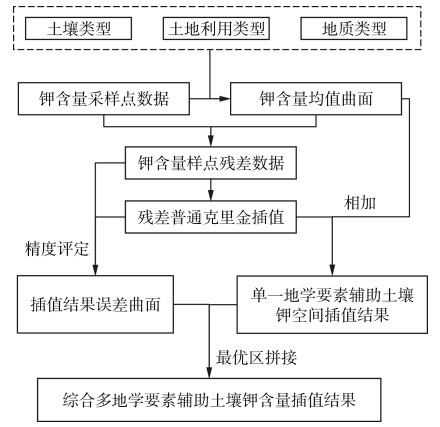 |
| 图 1 综合多种地学要素优化空间插值流程 Fig.1 Flow Chart of Spatial Interpolation Optimized by Multiple Geological Features |
通过实测样点数据计算出每种地学要素(土地利用类型、地质类型、土壤类型)下样点土壤钾含量的均值,获得与环境变量相关的钾含量均值曲面,见图 2。将样点数据与均值作差,得到样点钾含量残差数据,对其进行OK空间插值获得残差曲面,见图 3。将均值曲面与相应的残差曲面相加,得到单一地学要素辅助钾含量空间插值结果,见图 4。本文将土地利用类型辅助插值、地质类型辅助插值、土壤类型辅助插值、多地学要素辅助插值的方法分别称为OK_LANDUSE、OK_GEO、OK_SOIL、OK_GEOS。将提取样点处的插值结果与实测值作差,得到不同单一地学要素辅助空间插值的误差数据,利用该误差数据进行局部多项式插值,得到不同空间插值方法的误差曲面,见图 5。
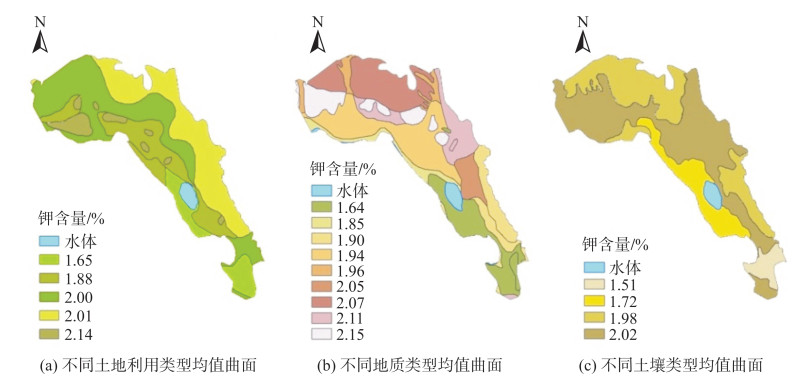 |
| 图 2 土壤钾含量在不同地学要素下的均值曲面 Fig.2 Mean Surfaces of Soil K Content Under Different Geological Factors |
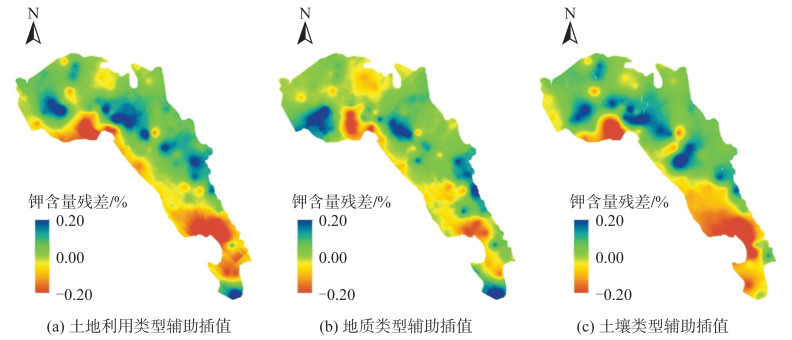 |
| 图 3 土壤钾含量残差OK空间插值结果 Fig.3 Spatial Interpolation Results of Soil K Content Obtained by OK |
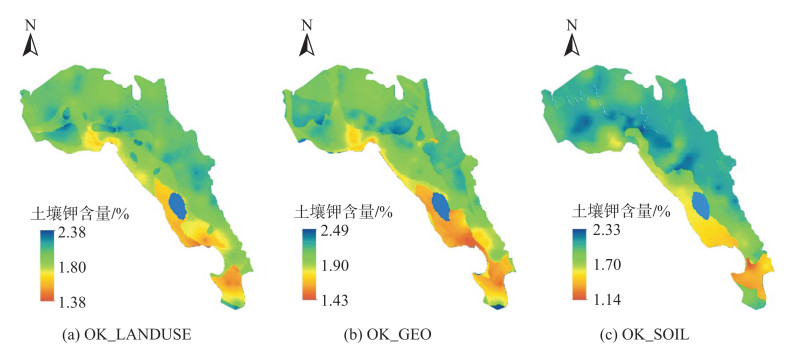 |
| 图 4 单一地学要素辅助的土壤钾含量空间插值结果 Fig.4 Spatial Interpolation Results of Soil K Content Obtained by Single Geological Factor-Assisted Methods |
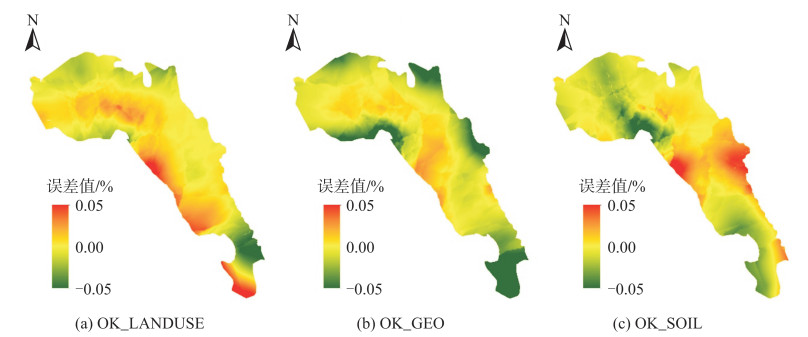 |
| 图 5 单一地学要素辅助空间插值方法的误差曲面 Fig.5 Error Surface of Single Geological Factor-Assisted Methods |
利用ArcGIS软件,基于栅格单元对比图 5的3个误差曲面,取误差值最小的栅格所对应的空间插值结果作为最优插值栅格进行拼接。基于栅格优选的方法原理见图 6;不同插值方法对应的最优分区见图 7;拼接结果(OK_GEOS结果)见图 8(a)。
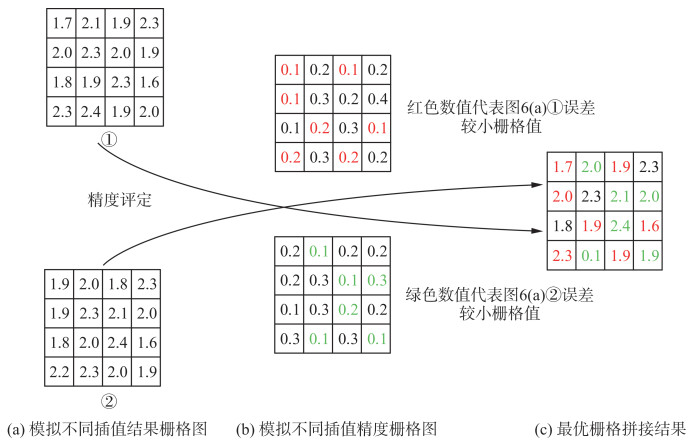 |
| 图 6 模拟基于栅格优选的最优插值过程 Fig.6 Simulation of Optimal Interpolation Process Based on Raster Preference |
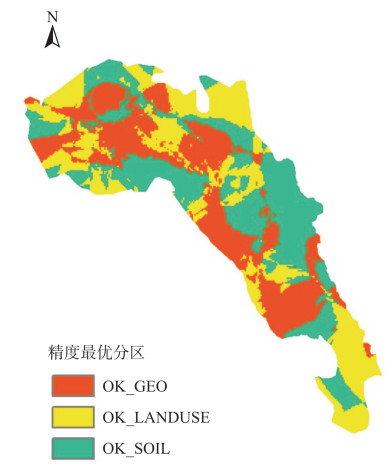 |
| 图 7 不同地学要素辅助的空间插值方法优选区域分布 Fig.7 Distribution of Preferred Regions of Spatial Interpolation Methods Assisted by Different Geological Factors |
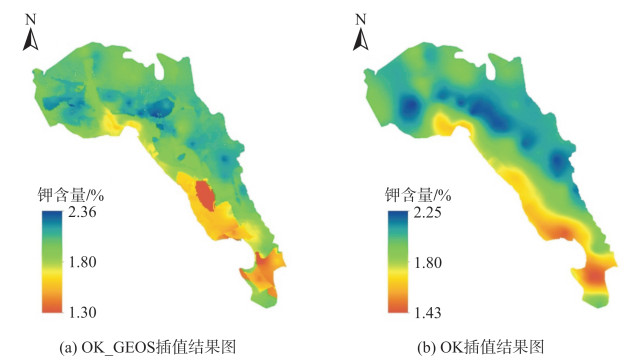 |
| 图 8 两种方法结果对比 Fig.8 Comparison of Results Obtained by Two Methods |
2 结果与分析 2.1 土壤钾含量的空间分异特征
从图 8(a)可以看出,总体上,研究区中部土壤钾含量较高,最大值在2.36%(23.6 g/kg)左右;东南部土壤钾含量较低,最低约1.3%(13 g/kg)。从细节上来看,土壤钾含量空间分异特征十分明显,在地学要素变化边界处存在突变。从图 8(b)可以看出,土壤钾含量总体分布趋势大致相同,但插值曲面较为平滑,空间分异刻画不够仔细。单一地学要素辅助插值的结果中,插值方法对空间分异特征的刻画上有了明显提升,不同地学要素边界处存在钾含量的突变。不足之处在于,复杂地学环境下的空间异质性规律仍刻画不够细致。某一地学要素下,其他环境因素对钾含量的影响并没有得到体现。综上所述,综合多地学要素辅助插值的方法能够更加清晰地反映复杂环境对土壤钾含量的空间分异的影响,更真实、细致地刻画土壤属性的真实分布规律。
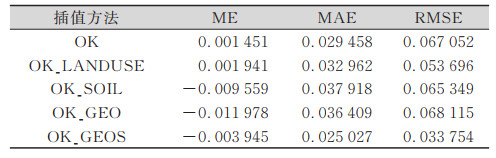
2.2 精度评价为定量描述综合地学要素插值方法的精度,通过计算预测结果的平均误差(mean error,ME)、平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)3种常用指标来检验不同方法的精度。对OK、OK_LANDUSE、OK_SOIL、OK_GEO、OK_GEOS的精度进行统计,结果见表 1。由于OK插值方法具有平滑效应,曲面的变异较真实值小[14],所得结果ME值最低,MAE值也低于其他3种插值方法,但RMSE值很高,仅低于OK_GEO。单一地学要素辅助插值方法中相对OK有明显精度提升的是OK_LANDUSE,其RMSE值降低约20%。OK_GEOS插值方法取得了最好的效果,相比单一地学要素辅助插值以及单一的全局插值方法,3个地学要素辅助插值的结果可使RMSE降低约50%,同时,MAE值也有所减小。可以看出,综合多地学要素辅助空间插值的方法能较大提高土壤钾含量插值的预测精度。
| 表 1 不同插值方法的精度 Tab.1 Accuracy of Different Interpolation Methods |
 |
3 结束语
研究区地理环境复杂多样,利用采样数据模拟研究区土壤属性空间分异格局意义重大。但使用单一全局空间插值或单一地学要素辅助空间插值的方法不能满足预测精度要求。基于已有研究成果,本文对综合多种地学要素的优化空间插值方法进行探究,提出了基于栅格单元优化综合多地学要素的空间插值方法。
不同地学环境会对土壤属性空间分异格局产生影响,不同插值方法都有其适应的地学环境,结合不同地学要素进行插值,将优选插值结果进行组合能得到更优的模拟结果。经验证,基于栅格单元优选组合的方法使每种插值方法的最优区域拼接在了一起,极大提高了插值精度。综合多种地学要素的插值方法使插值结果在空间分异特征的刻画上更加细致。因此,综合考虑实验区环境的影响,选用适宜的空间插值方法并将其融合在一起是提高插值精度的一种重要方式。
| [1] |
龙军, 张黎明, 沈金泉, 等. 复杂地貌类型区耕地土壤有机质空间插值方法研究[J]. 土壤学报, 2014, 51(6): 1 270-1 281. |
| [2] |
Mzuku M, Khosla R, Reich R, et al. Spatial Variability of Measured Soil Properties Across Site-Specific Management Zones[J]. Soil Science Society of America Journal, 2005, 69(5): 1 572-1 579. DOI:10.2136/sssaj2005.0062 |
| [3] |
史文娇, 岳天祥, 石晓丽, 等. 土壤连续属性空间插值方法及其精度的研究进展[J]. 自然资源学报, 2012, 27(1): 163-175. |
| [4] |
Triantafilis J, Odeh I O A, McBratney A B. Five Geostatistical Models to Predict Soil Salinity from Electromagnetic Induction Data Across Irrigated Cotton[J]. Soil Science Society of America Journal, 2001, 65(3): 869-878. DOI:10.2136/sssaj2001.653869x |
| [5] |
Kuriakose S L, Devkota S, Rossiter D G, et al. Prediction of Soil Depth Using Environmental Variables in an Anthropogenic Landscape: A Case Study in the Western Ghats of Kerala, India[J]. CATENA, 2009, 79(1): 27-38. DOI:10.1016/j.catena.2009.05.005 |
| [6] |
Hengl T, Heuvelink G B M, Rossiter D G. About Regression-Kriging: From Equations to Case Studies[J]. Computers & Geosciences, 2007, 33(10): 1 301-1 315. |
| [7] |
Penížek V, Borůvka L. Soil Depth Prediction Supported by Primary Terrain Attributes: A Comparison of Methods[J]. Plant, Soil and Environment, 2011, 52(9): 424-430. DOI:10.17221/3461-PSE |
| [8] |
朱阿兴, 李宝林, 杨琳, 等. 基于GIS、模糊逻辑和专家知识的土壤制图及其在中国应用前景[J]. 土壤学报, 2005, 42(5): 844-851. DOI:10.3321/j.issn:0564-3929.2005.05.019 |
| [9] |
Liu W, Du P J, Zhao Z W, et al. An Adaptive Weighting Algorithm for Interpolating the Soil Potassium Content[J]. Scientific Reports, 2016, 6: 23889. DOI:10.1038/srep23889 |
| [10] |
Liu W, Du P J, Wang D C. Ensemble Learning for Spatial Interpolation of Soil Potassium Content Based on Environmental Information[J]. PLoS One, 2015, 10(4): e0124383. DOI:10.1371/journal.pone.0124383 |
| [11] |
Panagopoulos T, Jesus J, Antunes M D C, et al. Analysis of Spatial Interpolation for Optimising Management of a Salinized Field Cultivated with Lettuce[J]. European Journal of Agronomy, 2006, 24(1): 1-10. DOI:10.1016/j.eja.2005.03.001 |
| [12] |
Zhang H R, Lu L J, Liu Y H, et al. Spatial Sampling Strategies for the Effect of Interpolation Accuracy[J]. IJGI, 2015, 4(4): 2 742-2 768. DOI:10.3390/ijgi4042742 |
| [13] |
李新, 程国栋, 卢玲. 空间内插方法比较[J]. 地球科学进展, 2000, 15(3): 260-265. DOI:10.3321/j.issn:1001-8166.2000.03.004 |
| [14] |
谢云峰, 陈同斌, 雷梅, 等. 空间插值模型对土壤Cd污染评价结果的影响[J]. 环境科学学报, 2010, 30(4): 847-854. |
 2022, Vol. 47
2022, Vol. 47


