| 抗差估计结合ObjectARX. NET技术在坐标转换中的应用 |
2. 义乌市地理信息中心,浙江 义乌,322000;
3. 义乌市勘测设计研究院,浙江 义乌,322000
2. Yiwu Geomatics Center, Yiwu 322000, China;
3. Yiwu Design and Research Institute of Exploration and Surveying, Yiwu 322000, China
为满足城市建设需要,我国使用的坐标系统有1954北京坐标系、1980西安坐标系以及各个城市的地方独立坐标系,随着2000国家坐标系在全国范围内全面启用,以往坐标系统纷纷退出历史舞台[1-3]。在投影中央子午线相同的前提下,将原有坐标系统转换为国家2000坐标系的过程中,经常会遇到选取的公共点坐标精度不一致,公共点误差较大,公共点控制范围不够等众多原因,从而导致转换的坐标精度低的问题。经典参数转换模型[4]采用最小二乘法,其抗粗差性能较弱,一旦公共点存在粗差,会出现病态转换模型,可能导致整个转换结果无法达到精度要求。因此本文提出基于选权迭代法改进模型来提高坐标转换模型的抗粗差能力,进一步提高坐标转换的精度。
1 经典坐标转换模型坐标转换模型应用最为广泛的有四参数模型、七参数模型,在区域坐标转换过程中,四参数模型因其转换精度较高,简便易掌握而被采用。四参数转换模型是将不同的高斯投影平面坐标利用2个平移参数、1个旋转参数和1个尺长因子进行转换。其数学模型如下:
| $ \left[ \begin{array}{l} {X_2}\\ {Y_2} \end{array} \right] = \left[ \begin{array}{l} \Delta {x_0}\\ \Delta {y_0} \end{array} \right] + \left( {1 + m} \right)\mathit{\boldsymbol{R}}\left( \theta \right)\left[ \begin{array}{l} {X_1}\\ {Y_1} \end{array} \right] $ | (1) |
| $ {\mathit{\boldsymbol{R}}_{(\theta )}} = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right] $ | (2) |
式中,X1、Y1为待转换坐标;X2、Y2为目标转换坐标;∆x0、∆y0为平移参数;m为尺长因子;R(θ) 为旋转矩阵。
由误差方程:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B}} \times \delta \mathit{\boldsymbol{X}} + \mathit{\boldsymbol{L}} $ | (3) |
| $ \left[ {\begin{array}{*{20}{c}} {{V_{{x_{12}}}}}\\ {{V_{{y_{12}}}}}\\ \vdots \\ {{V_{{x_{n2}}}}}\\ {{V_{{y_{n2}}}}} \end{array}} \right] = - \left[ {\begin{array}{*{20}{c}} 1&0&{ - {y_1}}&{{x_1}}\\ 0&1&{{x_1}}&{{y_1}}\\ \vdots & \vdots & \vdots & \vdots \\ 1&0&{ - {y_n}}&{{x_n}}\\ 0&1&{{x_n}}&{{y_n}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {x_0}}\\ {\Delta {y_0}}\\ a\\ b \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{x_{12}}}\\ {{y_{12}}}\\ \vdots \\ {{x_{n2}}}\\ {{y_{n2}}} \end{array}} \right] $ | (4) |
式中,a = (1 + m) cos θ,b = (1 + m) sin θ。由间接平差法及最小二乘法可计算四参数,其公式为:
| $ {\mathit{\boldsymbol{X}}_0} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $ | (5) |
其中,
利用两个以上公共点,根据式(5)可以计算出经典坐标转换四参数。
2 选权迭代法的抗差估计算法在实际测量工作中,通常选取的坐标转换公共点没有理论上的精度,经常会混入一些粗差点,如若采用经典坐标转换模型进行转换,根据现代测量平差理论[5],由于最小二乘法抗粗差性能差,公共点的精度较低或误差较大势必会降低整个模型的转换精度。
选权迭代法的抗差估计是利用权函数对公共点进行重新定权比,降低粗差公共点在参数计算中的作用,以此来提高转换模型的精度。先利用最小二乘法解算的参数估值对公共点进行坐标转换,当某个公共点精度较低,坐标转换后的估值与原值差值较大,则认为此公共点存在异常,根据选权迭代法重新定权,重新解算参数估值。
令
| $ \mathit{\boldsymbol{\tilde P = \omega P}} $ | (6) |
式中,
1)Tukey权函数法:
| $ {\bar \omega _i} = \left\{ {\begin{array}{*{20}{l}} {{{\left( {1 - {{\left( {{v_i}/{c_0}} \right)}^2}} \right)}^2}, \left| {{v_i}} \right| \le {c_0}}\\ {0, \;\;\left| {{v_i}} \right| > {c_0}} \end{array}} \right. $ | (7) |
2)Huber权函数法:
| $ {\bar \omega _i} = \left\{ {\begin{array}{*{20}{l}} {1, \;\left| {{v_i}/{\sigma _0}} \right| \le {c_0}}\\ {{c_0}/\left( {\left| {{v_i}/{\sigma _0}} \right|} \right), \left| {{v_i}/{\sigma _0}} \right| > {c_0}} \end{array}} \right. $ | (8) |
3)IGG1权函数法:
| $ {\bar \omega _i} = \left\{ {\begin{array}{*{20}{l}} {1, \left| {{v_i}} \right| \le {k_0}}\\ {{k_0}||{v_i}\left| {, {k_0} < } \right|{v_i}\mid \le {k_1}}\\ {0, \left| {{v_i}} \right| > {k_1}} \end{array}} \right. $ | (9) |
式中,c0、k0、k1称为调和系数;σ0为公共点中误差。
选权迭代坐标转换模型的计算方法与步骤:
1)初始默认公共点精度相同,制定初始权矩阵P0为单位矩阵;
2)运用式(5)计算初始4个参数值,并求出公共点拟合残差,根据选权迭代法式(7)~式(9),选择合适方案,计算调节权重比因子ω,代入式(6)求出新的权矩阵P1;
3)多次重复步骤2),直至4个参数值的2次迭代变化值小于δ(一般取δ = 10-4)停止迭代,得到的最终拟合参数即为最终值。
进行迭代解算时,由于迭代次数较多,需要选择合适的编程语言进行解算,MATLAB在解算矩阵运算时,简洁快速,但要与ObjectARX. NET技术结合难度较大,同时MATLAB软件庞大不利于快速安装使用。因此,选择采用. NET作为开发平台,编程语言采用C#,在进行矩阵解算时,引入MathNet外部接口,其中LinearAlgebra.Double和LinearAlgebra.Generic两个函数类提供了选权迭代运算需要的各矩阵运算方法。
3 ObjectARX. NET技术实现坐标转换测量中大量的图件是使用AutoCAD进行数字化存储,对AutoCAD图件进行坐标转换,国内已有大量科研工作者发表相关文献[7-11],但大多数是将AutoCAD图件存储为dxf格式文件,dxf文件是二进制格式,通过分析dxf文件中的“组码”,应用编程语言提取相应节点坐标,对节点坐标进行坐标转换,得到的新坐标替换原dxf文件中的节点坐标,以此来实现AutoCAD图件的坐标转换工作。此方法在处理过程中需要遍历整个dxf文件组码,根据“组码”特征值分多种情况进行实体节点坐标转换,整个过程转换关系复杂,考虑因素众多,且用户界面互操作性差,无法依据用户要求选择指定图元进行坐标转换。
本文使用ObjectARX. NET技术生成动态数据链接库DLL文件,进行AutoCAD图件的坐标转换工作。AutoCAD二次开发工具有VBA、LISP和ObjectARX,其中ObjectARX功能强大,快速访问图形数据库,在. NET框架下使用ObjectARX能够支持创建用户界面、访问数据库并支持开发大型程序。ObjectARX. NET技术实现坐标转换的核心方法为:AutoCAD的dwg格式主要由实体对象(如线、圆弧、文本文件等)及非实体对象(如颜色、线宽、图层等)构建而成。每一个实体对象有唯一的标识码ObjectID,可以通过ObjectARX提供的GetObject()函数获取相应实体,再对实体进行坐标转换。在ObjectARX专门提供了仿射变换TransformBy ()函数与Matrix3d()(三维矩阵)类,Matrix3d类可以用于几何对象的平移、旋转、投影、缩放、镜像等功能。通过测量学中四参数模型将平移、旋转、缩放的参数解算出来,再将其代入Matrix3d类函数以此实现坐标转换工作,测量学四参数模型与仿射变换三维矩阵转换函数式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Matrix3d}}\;{\rm{zbcs = Matrix3d}}{\rm{.Scaling(scaleFactor}}, {\rm{movepoint)}}{\rm{.}}\\ \;\;{\rm{PostMultiplyBy(Matrix3d}}{\rm{.Rotation(rotateAngle}}, {\rm{Vector3d}}{\rm{.ZAxis}}, {\rm{movepoint))}}{\rm{.}}\\ {\rm{PostMultiplyBy}}\left( {{\rm{Matrix3d}}{\rm{.Displacement}}\left( {{\rm{ moveStartPnt}}{\rm{.GetVectorTo}}\left( {{\rm{ movepoint }}} \right)} \right)} \right); \end{array} $ |
上述函数式中movepoint为四参数求解得到的(∆y0,∆x0),因大地测量坐标系与AutoCAD成图坐标系中X、Y方向相反,在此要变换;moveStartPnt为原转换坐标原点(0,0);rotateAngle为四参数解算的旋转角θ;scaleFactor为四参数解算的尺长因子m;Displacement()为平移函数;Rotation()为旋转函数;Scaling ()为缩放函数。
因四参数转换过程中不涉及Z值的转换,在变换过程中先获取实体Z值属性,最后再将其数值赋回。结合抗差估计算法的整个转换流程如图 1所示。
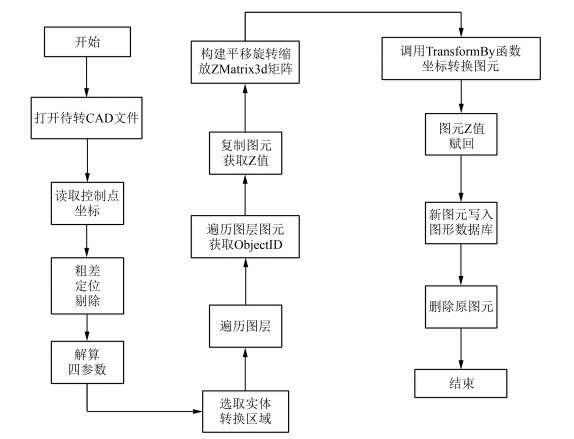 |
| 图 1 图件转换流程 Fig.1 Flow Chart of Map Conversion |
4 CAD中坐标转换功能实现
1)控制点坐标录入。
本程序提供两个控制点录入方式,一是事先编写txt文本文件,根据文本文件录入控制点坐标,二是直接根据DWG文件在图件上拾取控制点坐标信息。
2)粗差探测及参数解算。
根据控制点坐标录入信息及抗差估计算法,提供4种抗差估计算法模型,进行粗差的探测及剔除粗差后,参数解算结果同时具有图元坐标转换及存盘功能。
3)转换实体精度分析。
利用本文研制的软件与现今应用广泛的Arc⁃ GIS、南方CASS软件进行坐标转换成果比较,验证软件的可行性,通过转换控制点中有粗差和无粗差两种情况进行精度分析,具体结果见表 1。
| 表 1 图件转换坐标检测差值/mm Tab.1 Test of the Coordinates of Map Conversion/mm |
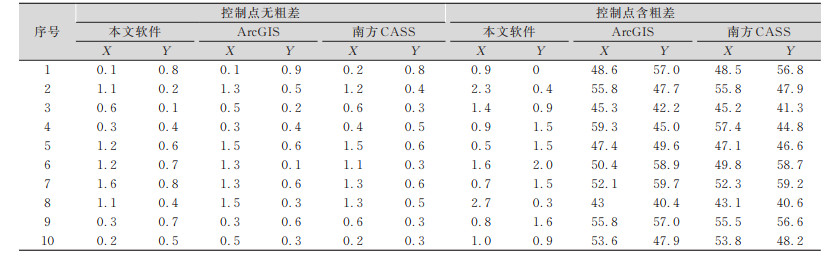 |
对表 1特征点进行坐标转换中误差计算可知,在控制点无粗差的情况下,本文研制的软件与Arc⁃ GIS、南方CASS软件在图件转换精度上高度吻合,中误差在2 mm以内,表明本文软件具有可行性,在图件转换过程中不存在额外精度损失,转换方式可行;当控制点中含有粗差,ArcGIS、南方CASS软件的转换精度明显下降,图件的转换中误差在5 cm以上,这两种软件不具有抵抗粗差的能力,而本文研制的软件转换的图件坐标精度损失不大,中误差控制在5 mm内,拥有抵抗粗差的能力。
5 结束语本文对经典四参数模型进行改进,提出抗差估计的迭代坐标转换模型。此模型与ObjectARX. NET技术结合研制了基于抗差估计算法的Auto⁃ CAD图件转换软件,经过与商业软件对比,本软件具有抵抗粗差的能力,图件转换精度较高。在局部区域控制点稀少同时掺入异常值时,本软件能发挥出抵抗粗差的性能,提高整体转换精度。随着2000国家坐标系使用,在偏远地区小范围勘查时,往往缺少高精度转换控制点的情况下,适宜采用此方法来提高整个转换区域的精度。
| [1] |
姚宜斌. 平面坐标系统相互转换的一种简便算法[J]. 测绘信息与工程, 2001, 26(1): 1-3. |
| [2] |
倪飞, 崔桂官. 平面坐标转换的内插算法[J]. 测绘信息与工程, 2011, 36(3): 33-35. |
| [3] |
束蝉方, 李斐, 沈飞. 空间直角坐标向大地坐标转换的新算法[J]. 武汉大学学报·信息科学版, 2009, 34(5): 561-563. |
| [4] |
何林, 柳林涛, 许超钤, 等. 常见平面坐标系之间相互转换的方法研究--以1954北京坐标系、1980西安坐标系、2000国家大地坐标系之间的平面坐标相互转换为例[J]. 测绘通报, 2014(9): 6-11. |
| [5] |
张勤, 张菊清, 岳东杰, 等. 近代测量数据处理与应用[M]. 北京: 测绘出版社, 2011: 94-95.
|
| [6] |
王新洲. 高等测量平差[M]. 北京: 测绘出版社, 2006: 87-93.
|
| [7] |
汪燕麟, 刘鸿飞, 王利华, 等. 基于DWG文件的图件坐标转换方法研究与实现[J]. 测绘地理信息, 2016, 41(6): 82-85. |
| [8] |
李芳珍, 许伦辉. DXF文件格式及其外部接口的研究[J]. 兵工自动化, 2008(7): 83-85. |
| [9] |
姚宜斌, 孔建. 基于DXF文件的图件转换方法研究及程序实现[J]. 大地测量与地球动力学, 2011, 31(1): 117-122. |
| [10] |
童话, 李建华, 徐凯. AutoCAD表格图形文件中的数据读取[J]. 机械设计与制造, 2005(7): 67-68. |
| [11] |
王小华, 程传录, 范宏涛, 等. 基于AutoCAD. NET API的地形图坐标转换实现方法研究[J]. 测绘与空间地理信息, 2013, 36(11): 58-60. |
 2022, Vol. 47
2022, Vol. 47

