| 基于三维激光扫描技术的桥塔挠度测量 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079;
3. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
桥塔作为桥梁的主要承重部分,其健康状况直接决定着整座桥梁的可用性,桥塔挠度的变形是评价桥塔使用功能和安全性的重要指标之一。因此,桥塔挠度测量方法的研究以及相应检测仪器的研制对于桥梁的安全运营有着极其重要的作用[1]。在桥梁垂直向挠度 (如桥面) 监测中,常用的测量仪器有百分表、千分表、挠度仪,测量方法有光电图像法、GPS法、连通管法、高精度水准测量、全站仪测量等[2-4]。对桥梁水平向挠度 (如桥塔),目前最常用的测量手段仍然是全站仪为主,其精度高,但需要安装棱镜,测点数量也有限,难以反映挠度的整体变化。桥塔挠度的测量主要是指桥梁承受静态荷载或动态荷载情况下桥塔的几何弯曲情况。作为非接触式测量的代表,地面三维激光扫描仪可以快速、准确地获取海量的三维点云数据[5]。通过数据处理手段,可以准确地获取桥塔整体和细节的信息,从而实现桥塔挠度及其变化的测量。
1 数据采集某斜拉桥在通车前进行静态荷载试验,试验时间为凌晨前后,大气活动较为稳定。采用三维激光扫描仪RIEGL VZ400(标称精度为100 m内的点位精度±2 mm) 对桥塔进行扫描,设置桥塔中部的点云扫描间隔为5 cm。受观测现场条件的限制,扫描仪架设在堤岸上,桥塔的实际扫描范围如图 1所示。其中,扫描的最远处 (塔左顶部) 近290 m,最近处 (塔右底部) 约210 m。本次试验共进行了6个时段的扫描测量:时段1和时段2为空载时进行的扫描,即在荷载加载前进行的扫描;时段3为半载时进行的扫描;时段4为满载时进行的扫描;时段5和时段6为卸载后的扫描。
 |
| 图 1 桥体的扫描点云 Figure 1 Scanned Point Cloud of Bridge |
时段1扫描的点云如图 1所示。为方便表达变形,将点云坐标由扫描仪坐标系转换至桥轴坐标系:桥塔横梁上表面几何中心为原点O,天顶方向为Z轴,桥轴线为X轴,右手定则确定Y轴。后文所用到的点云坐标均是转换到桥轴坐标系后的坐标。
2 数据处理斜拉桥桥塔通过拉索承载桥梁及桥上荷载,它会随着荷载的变化而发生挠度变化。因此,通过分析桥塔在加载荷载前后其不同高度部位的水平位移,便可得到其挠度及其变化。为了反映桥塔整体的挠度变化,以桥塔的各个棱线为研究对象,计算各条棱线的挠度值。桥塔 (如图 2(a)所示) 在时段1所获取的点云如图 2(b)所示。为了便于后面说明,将靠近扫描仪一侧的4条塔桥棱线 (从Y轴正向开始) 分别命名为棱线a、棱线b、棱线c和棱线d。
 |
| 图 2 桥塔及其点云数据 Figure 2 Pylon and Its Point Cloud |
在计算各棱线的挠度值之前,首先要从桥塔点云中提取各棱线对应的点云。但扫描时,扫描点不会准确地落在棱线上,而是基本上都在棱线附近,因此,实际获取的棱线点是折线状的。为了准确地表达棱线,需要对这些点进行处理。
2.1 棱线的提取对于棱线a和棱线c等桥塔点云的边缘线,可采取两类方法提取[6-9]:一类是将散乱的点云三角化处理后得到三角网格模型进行提取;另一类是直接利用散乱的点云边界特征进行提取。基于三角网格模型提取点云边界的方法精度较高,但是建立三角格网的过程比较复杂,耗时较长,难度较大。而利用散乱点直接提取,虽然精度略低,但过程简便,通过后期处理,同样可以准确获取边界线。
对任意的非边界点pi,其邻域内的点基本是均匀分布。因此,点pi与其邻域点构成的向量 (投影至这些点的拟合平面上) 之和不会超过一定的值。据此,本文选用了第二类方法。对文献[9]的方法加以改进,设计如下算法:①以点pi及邻域点拟合空间平面M;②求解平面M的法向量n;③将点pi及邻域点沿n投影至平面M上;④以点pi的投影点pi′为原点,以点pi′及离该点最远的投影点 (点pi的邻域点在M上的投影点) 的连线为X轴正向,以垂直于X轴的方向为Y轴建立右手平面直角坐标系;⑤将各投影点坐标转换至平面直角坐标系内;⑥在平面坐标系内,求解原点与投影点构成的平面向量,并对其单位化;⑦将这些单位向量进行矢量相加后,投影至X轴和Y轴上;⑧将投影至坐标轴上的向量与阈值比较,判定点pi是否为边界点。
以时段1为例,通过该方法获取的边界点如图 3(a)所示,人工去噪后的结果如图 3(b)所示。
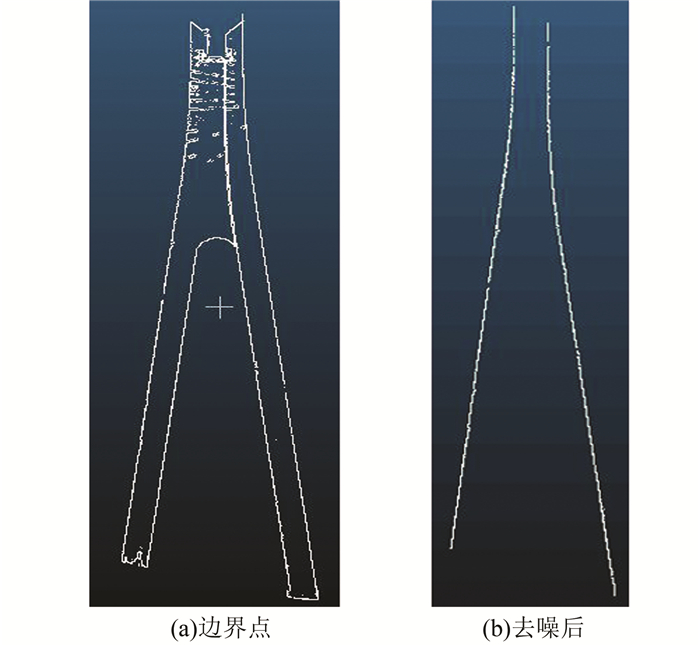 |
| 图 3 棱线a和棱线c上提取的点 Figure 3 Extracted Points of a and c Boundaries |
棱线b和d是两个扫描面的相交线。但两个实际面是未知的数学曲面,无法通过数学曲面求解得到交线。为此,对于棱线b,先提取出ab线所在的曲面点云,再通过上述提取边界点的方法提取棱线b。同样的方法提取棱线d,不再赘述。
2.2 棱线的拟合由于所获取到的棱线点云是折线状,为分析方便,将各个棱线点云进行曲线拟合。
首先将各条棱线的点云进行去噪,然后将点云向XZ平面进行投影。以X为自变量,Z为因变量进行二元多项式拟合。为了避免过度拟合,多项式的阶数k按照AIC (Akaike information criterion) 原则确定为:
| $ {\rm{AIC}} = 2k + n{\rm{ln}}(S/n) $ | (1) |
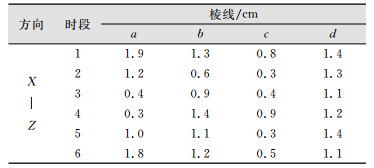
式中,k为多项式阶数;n为参与拟合的点数;S为拟合的残差平方和。最终各条棱线拟合后,拟合精度都在2 cm以内,中误差如表 1所示。
| 表 1 4条棱线拟合后中误差 Table 1 Fitted Mean Square Error of Four Crest Lines |
 |
3 结果分析 3.1 挠度变化的测量精度
为了衡量三维激光扫描技术在桥塔挠度测量中的精度,将时段1获取的棱线和时段2所获取的棱线进行比较验证。由于时段1和时段2都是空载情况下的测量,观测时间间隔较短,认为桥塔没有变形,因此,可通过计算同一个点的坐标差的中误差衡量本次挠度变化测量的内符合精度。
每条棱线上选取101个监测点,求解第i个监测点的误差为:
| $ {{\mathit \Delta} _i} = \sqrt {{{\left( {{X_{i1}} - {X_{i2}}} \right)}^2} + {{\left( {{Y_{i1}} - {Y_{i2}}} \right)}^2}} $ | (2) |
式中,Xi1、Yi1分别为第i点在时段1的X、Y坐标值;Xi2、Yi2分别为第i点在时段2的X、Y坐标值。各条棱线点的均值和中误差为:
| $ \left\{ \begin{array}{l} d = \sum\limits_{i = 1}^{101} {\left( {\left( {{X_{i1}} - {X_{i2}}} \right) + \left( {{Y_{i1}} - {Y_{i2}}} \right)} \right)/101} \\ \sigma = \sqrt {\sum\limits_{i = 1}^{101} {\left( {{\Delta _i}{\Delta _i}} \right)/100} } \end{array} \right. $ | (3) |
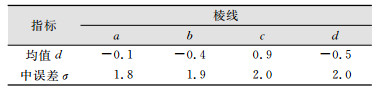
4条棱线两次测量对比均值和中误差如表 2所示。由表 2可看出,4条棱线在时段1、时段2的坐标差均值在1 cm内,中误差在±2 cm内,也就是挠度变化测量的内符合精度为±2 cm。
| 表 2 4条棱线两次测量对比均值和中误差/cm Table 2 Mean and Mean Square Error of Four Crest Lines During Two Periods/cm |
 |
3.2 桥塔挠度分析
将4条棱线分别进行如下处理:在XZ投影面上,以时段1、时段2的X坐标的均值为基准值,将时段3、时段4以及时段5、6的均值分别与该基准值作差,结果如图 4所示。其中,图 4(a)~图 4(d)依次对应棱线a~d。图例中的3、4、5分别对应时段3、时段4、时段5、6的均值的处理结果。
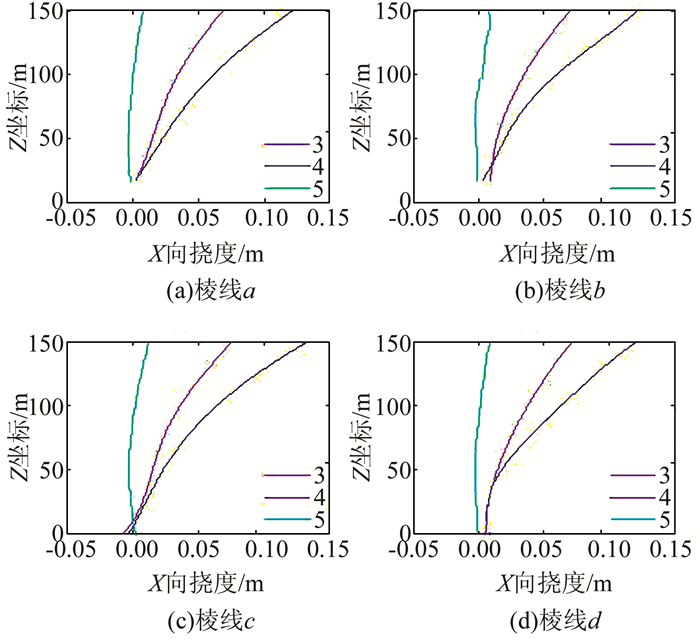 |
| 图 4 4条棱线在XZ平面上的投影的变形曲线 Figure 4 Projected Deformation Curves of Four Ridge Lines on the Plane XZ |
图 4中a、b、c、d线在同一时段的挠度值曲线分别如图 5(a)~5(c)所示。
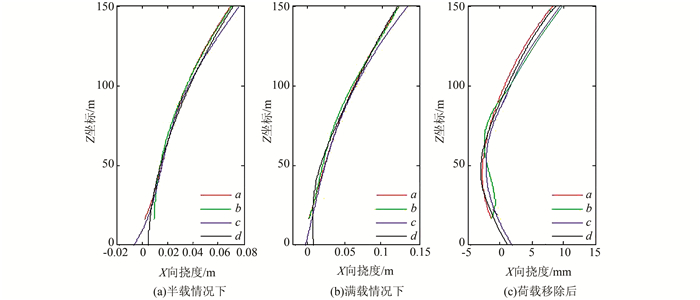 |
| 图 5 不同荷载情况下各棱线在XZ平面上的投影的挠度曲线 Figure 5 Deflection of Four Ridge Lines in XZ Direction with Different Loads |
1)图 4中时段3(粉红色) 和时段4(蓝色) 分别对应半载、满载情况下桥塔棱线在桥轴竖面的整个实测挠度曲线,由此可以看出,桥塔挠度会随着荷载和高度的增加而加大,而且所呈现的连续变化是曲线而非直线。对于顶部而言,半载时偏移8 cm左右;满载时偏移12 cm左右。
2) 从图 4和图 5(c)中可以看出,荷载移除后的挠度并没有回到初始位置,顶部偏值在7 mm左右。离桥面48 m处存在一个明显的小拱形。这里面除了存在测量与计算误差外,不排除桥塔可能存在的微小塑性形变。
3) 由图 5可以看出,两根塔柱在各个状态下的几何变化具有较好的相似性和一致性,说明两根塔柱施工结构相当,静态荷载下受力比较均匀。
综上所述,利用地面三维激光扫描技术可以获取桥塔的细节挠度,从而实现对桥塔整体变形的把握。由于扫描密度不够 (本次扫描间隔为5 cm),同时测量时桥梁离正式通车还有一段时间,一些脚手架和吊架影响了点云的质量,导致边界点提取精度降低,在一定程度上降低了本次挠度测量的精度。
4 结束语在本次试验中,利用三维激光点云对近堤岸桥塔进行了扫描,以具有代表性的4条棱线的挠度来反映桥塔的挠度变化。从试验结果可以看出,200多米的距离,通过数据处理,可以获得2 cm内的棱线挠度拟合精度;在桥梁有荷载时,桥塔棱线变化趋势明确,反映了桥塔整体挠度的合理变化。以上结论反映出本文所采用的三维激光扫描技术及相应的数据处理方法合理,可为桥塔挠度的测量提供新的技术手段。
需要注意的是,由于点云扫描密度不够,使得棱线点云提取的精度受到一定的影响。此外,三维激光扫描易受外界环境的影响,在数据精度上仍有不足。因此,该方法应该作为现有挠度监测手段的一种补充,相应的数据处理方法在实用中仍有待改进。
| [1] |
王磊. 大型桥梁健康监测中挠度测量技术研究[D]. 南京: 东南大学, 2006 |
| [2] | 曾威, 于德介, 胡柏学, 等. 基于连通管原理的桥梁挠度自动监测系统[J]. 湖南大学学报 (自然科学版), 2007, 34(7): 44–47 |
| [3] | 黄声享, 罗力, 何超. 地面微波干涉雷达与GPS测定桥梁挠度的对比试验分析[J]. 武汉大学学报·信息科学版, 2012, 37(10): 1 173–1 176 |
| [4] | 吕长荣, 卓秋林, 徐嵩基. 智能全站仪在大型桥梁挠度观测中的应用[J]. 山东交通学院学报, 2009, 17(2): 50–55 |
| [5] | 徐进军, 廖骅, 韩达光, 等. 大跨度桥梁桥面线形测量新方法[J]. 测绘通报, 2016, (1): 91–94 |
| [6] | Zhang Hongxin. Semi-Stationary Subdivision Operators in Geometric Modeling[J]. Progress in Natural Science, 2002, 12(10): 772–776 |
| [7] | 宋大虎, 李忠科, 孙玉春. 三维散乱点云快速曲面重建算法[J]. 计算机应用研究, 2013, 30(8): 2 527–2 529 |
| [8] | 孙殿柱, 范志先, 李延瑞. 散乱数据点云边界特征自动提取算法[J]. 华中科技大学学报 (自然科学版), 2008, 36(8): 82–84 |
| [9] |
晏海平. 散乱点云边界提取及孔洞修复算法研究[D]. 南昌: 南昌大学, 2014 |
 2017, Vol. 42
2017, Vol. 42

