| BDS/GPS兼容接收机噪声检测方法研究 | [PDF全文] |
随着卫星导航定位系统从单一的GPS时代向多星座并存的GNSS时代转移,多星座兼容接收机将会成为未来接收机产品的主流。衡量接收机最重要的指标——原始观测值噪声的优劣程度就显得尤为重要。目前,关于GNSS(global navigation satellite system)接收机噪声水平检测方法主要以“超短基线比对检验法”和“零基线检测法”[1]为主,超短基线差分方法不能完全消除两个接收机的有色噪声[2-7]。已有的检测方法大多针对单一GPS接收机,本文采用零基线双差法与单站法对BDS/GPS兼容接收机的内部噪声与系统噪声的检测方法进行了探讨,对比分析了BDS/GPS双系统的伪距观测值和载波相位观测值的噪声。
1 接收机内部噪声检测方法 1.1 零基线双差法零基线是指两个接收机通过功分器共用一个天线,即两个接收机天线之间的基线长度为零[8-11]。零基线检验法可以突出地反映各通道间时延差异以及由接收机间时钟偏差、延迟锁相环和相位锁定环误差引起的观测值噪声。简而言之,零基线能够较真实地反映接收机的质量水平。但是零基线检验法求出的结果,仅仅反映两台接收机主机的噪声水平,实际上排除了天线的因素。图 1为零基线原理图。
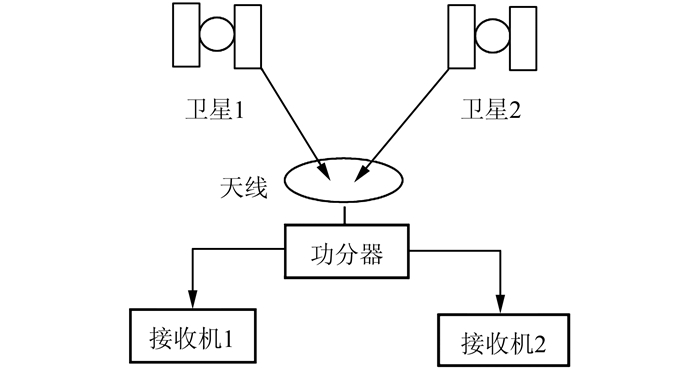 |
| 图 1 零基线检验原理图 Fig.1 Zero Baseline Test Schematic |
伪距观测值和载波相位观测方程为:
| $ \begin{array}{*{20}{c}} {P_i^p = \rho _i^p + d{\rho ^p} + c\left( {d{T^p} - d{T_i}} \right) + d_{i\;\;{\rm{ion}}}^p + }\\ {d_{i\;\;{\rm{trop}}}^p + \varepsilon _{i\;\;{\rm{mul}}}^p + \varepsilon _{i{\rm{ noize }}}^p} \end{array} $ | (1) |
| $ \begin{aligned} \varphi_{i}^{p}=& \frac{f}{c}\left(\rho_{i}^{p}+d \rho^{p}\right)-f\left(d T^{p}-d T_{i}\right)-N_{I}^{P}-\\ & \frac{f}{c}\left(d_{i \text { ion }}^{p}+d_{i \text { trop }}^{p}-\varepsilon_{i \text { mul }}^{p}-\varepsilon_{i \text { noize }}^{p}\right) \end{aligned} $ | (2) |
式中,Pip为接收机i到卫星p的伪距观测值;φip为接收机i到卫星p的相位观测值;ρip为几何距离;dρp为轨道误差;c为光速;dTp为卫星钟误差;dTi为接收机钟误差;di ionp为电离层延迟;di tropp为对流程延迟;εi mulp为多路径误差;εi noizep为伪距观测噪声,NIP为整周模糊度;εi noizep为相位观测噪声。
对式(1)进行双差处理,可得:
| $ \begin{aligned} \nabla \Delta P_{i j}^{p q}=& \nabla \Delta P_{i j}^{p}-\nabla \Delta P_{i j}^{q}=\\ & \varepsilon_{i \text { noize }}^{p}-\varepsilon_{j \text { noize }}^{p}-\varepsilon_{i \text { noize }}^{q}+\varepsilon_{j \text { noize }}^{q} \end{aligned} $ | (3) |
假设伪距测量噪声
| $ \sigma _{{\varepsilon _{{\rm{ noize }}}}}^2 = \sigma _{\varepsilon _{i~{\rm{ noize }}}^p}^2 = \sigma _{\varepsilon _{j~{\rm{ noize }}}^p}^2 = \sigma _{\varepsilon _{i~{\rm{ noize }}}^q}^2 = \sigma _{\varepsilon _{j~{\rm{ noize }}}^q}^2 $ |
根据误差传播定律可得:
同理,可以得到载波相位观测值噪声。由于整周模糊度的存在,双差后为波长的整数倍。为了直观显示,后续减去波长的整数倍。对式(2)进行双差,则有:
| $ \begin{aligned} \nabla \Delta \mathit{\Phi }_{i j}^{p q}=& \lambda\left(\nabla \Delta \varphi_{i j}^{p q}+\nabla \Delta N_{i j}^{p q}\right)=\\ & \varepsilon_{i \text { noize }}^{p}-\varepsilon_{j \text { noize }}^{p}-\varepsilon_{i \text { noize }}^{q}+\varepsilon_{j \text { noize }}^{q} \end{aligned} $ | (4) |
| $ {\sigma _{{\varepsilon _{{\rm{noize }}}}}} = \frac{{{\sigma _{\Delta \mathit{\Phi }}}}}{2} $ | (5) |
式中,p、q为卫星;i、j为接收机;σΔΦ为相位差分后的噪声中误差;εi noizep、εj noizep、εi noizeq、εi noizeq为观测噪声;σεnoize表示噪声中误差;∇ΔPijpq为双差伪距观测值;∇ΔΦijpq为双差测相伪距;∇Δφijpq为双差相位观测值;∇ΔNijpq为双差模糊度。
1.2 实例分析对2017年4月20日于某楼顶采集的一段静态数据进行分析。采用Trimble59800.00天线接收真实卫星信号,经过功分器将GNSS卫星信号分为两路,同时传送给一对Trimble Net R9型接收机或者一对某国产单频接收机SN,采样间隔为5 s。实验过程分为两个时段进行,如表 1所示,用零基线双差法处理静态测试原始观测量数据,对GPS G09、G23卫星与BDS C02、C03卫星进行分析。如图 2~图 4所示,横轴表示观测历元的个数;纵轴为载波相位观测值与码观测值噪声。
| 表 1 零基线测试时段 Tab.1 Zero Baseline Test Period |
 |
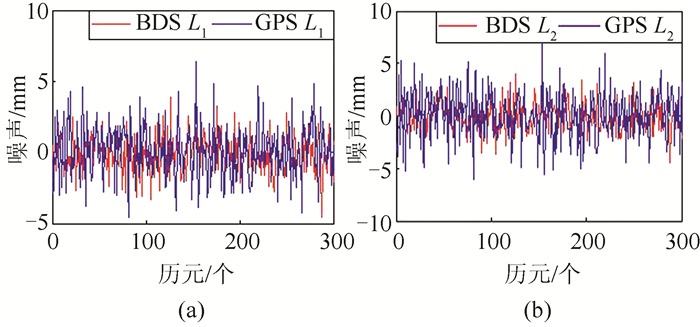 |
| 图 2 R9载波相位噪声 Fig.2 R9 Carrier Phase Noise |
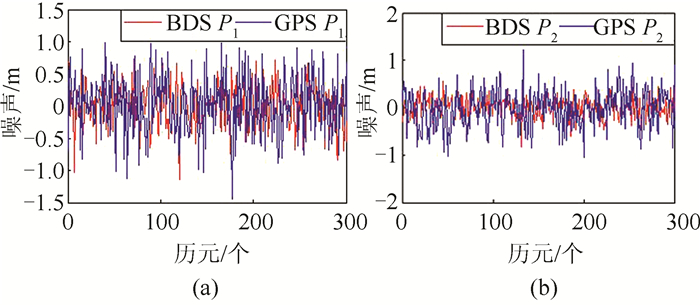 |
| 图 3 R9伪距噪声 Fig.3 R9 Pseudorange Noise |
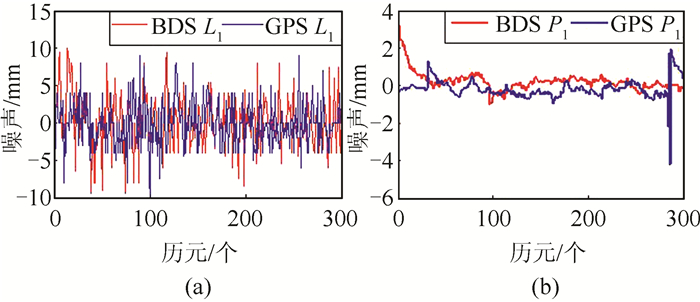 |
| 图 4 SN载波/伪距噪声 Fig.4 SN Carrier / Pseudo-Range Noise |
对图 2~图 4所描述噪声内符合精度进行计算,其结果如表 2所示。
| 表 2 伪距与载波观测值噪声RMS统计表 Tab.2 Pseudo Range and Carrier Noise RMS Statistics Table |
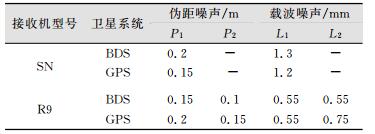 |
从表 2可以看出, SN接收机质量较差。BDS与GPS的噪声基本处于同一水平。对于伪距而言, P2码噪声略优于P1码噪声;对于载波而言,L1载波噪声与L2载波噪声无明显差别,且BDS与GPS系统具有一致性。
2 单站法检测系统噪声零基线检测法有以下4个局限性:
1) 只能检验天线与主机分离的接收机;
2) 只能检测接收机的内部噪声;
3) 所描述的是两台接收机相对质量的好坏,不能绝对的反映单台接收机的噪声水平;
4) 需要用到功分器,增加了一个噪声源。
综上所述,采用单站法检测接收机的系统噪声[12]。所谓系统噪声是指包括因接收机和天线内部电气性能引起的和因观测环境引起的测距和测相误差。系统噪声也称作测量噪声。
2.1 相位观测值噪声将双频测相伪距作差可得电离层残差组合(LG组合):
| $ \begin{aligned} L_{\mathrm{LG}}=& \lambda_{1} \varphi_{1}-\lambda_{2} \varphi_{2}=\\ & \frac{I}{f_{1}^{2}}-\frac{I}{f_{2}^{2}}+\lambda_{1} N_{1}+\lambda_{2} N_{2} \end{aligned} $ | (6) |
若电离层变化比较平缓,则相邻历元间的电离层延迟可以消除。将式(8)应用于t1、t2,在历元将作差,可得相位残差:
| $ \varepsilon^{\prime}=\frac{c}{f_{1}}\left(\varphi_{1}\left(t_{2}\right)-\varphi_{1}\left(t_{1}\right)\right)+\frac{c}{f_{2}}\left(\varphi_{2}\left(t_{1}\right)-\varphi_{2}\left(t_{2}\right)\right) $ | (7) |
又有ε′=ε1(t2)-ε1(t1)+ε2(t1)-ε2(t2)。
式(6)、式(7)中,I为电离层延迟,φ1、φ2分别为L1、L2载波相位观测值,N1、N2分别为L1载波与L2载波整周模糊度,ε1(t1)、ε1(t2)、ε2(t1)、ε2(t2)分别为不同历元下L1载波与L2载波的噪声,假设L1载波噪声ε1与L2载波噪声ε2相等,即ε1(t1)=ε1(t2)=ε2(t1)=ε2(t2),则由误差传播定律可得:ε1=
应当注意的是,此时求解的为L1载波与L2载波的混合噪声。
2.2 码观测值噪声码噪声的求解分为单频机和双频机两种情况。对于双频机而言,可用§2.1方法求解。也可应用下述单频机方法分别求出P1码与P2的噪声。对于单频机而言,可以运用测相伪距减码伪距组合求解码噪声,数学模型为:
| $ \varepsilon^{\prime}=\left(\frac{c}{f} \varphi\left(t_{2}\right)-P\left(t_{2}\right)\right)-\left(\frac{c}{f} \varphi\left(t_{1}\right)-P\left(t_{1}\right)\right) $ | (8) |
式中,
对2017年4月20日于某楼顶采集的一段静态数据进行分析,采用Trimble59800.00天线,R9型接收机,采样间隔5 s,观测时段内视野良好,无明显干扰。对BDS的C02、C03卫星与GPS的G07、G08卫星进行分析。如图 5~图 8所示,表 3给出了单站检测法检测的R9型接收机的伪距和载波噪声的内符合精度,其中P表示混合P码,L为混合载波。
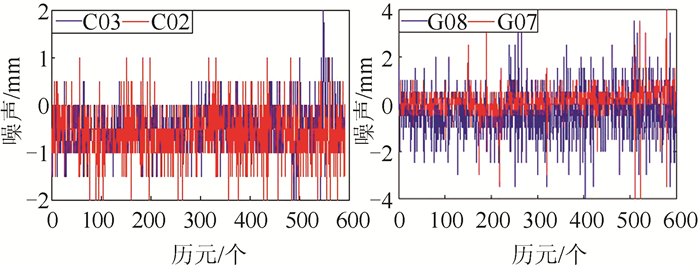 |
| 图 5 BDS/GPS相位观测值噪声序列 Fig.5 BDS/GPS Phase Observations of Noise Sequences |
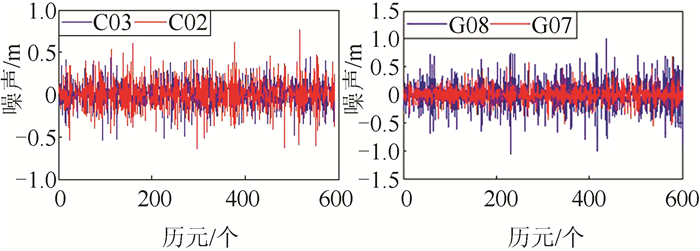 |
| 图 6 BDS/GPS码观测值噪声序列 Fig.6 BDS / GPS Code Observations Noise Sequence |
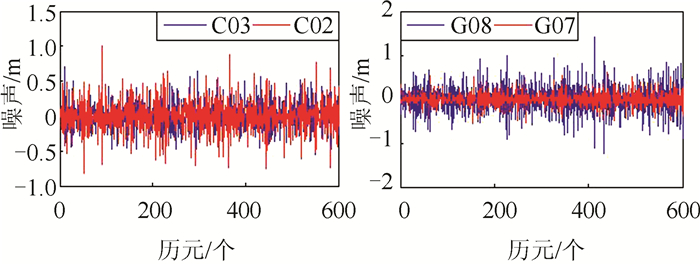 |
| 图 7 BDS/GPS P1码观测值噪声序列 Fig.7 BDS/GPS P1 Code Observed Value of the Noise Sequence |
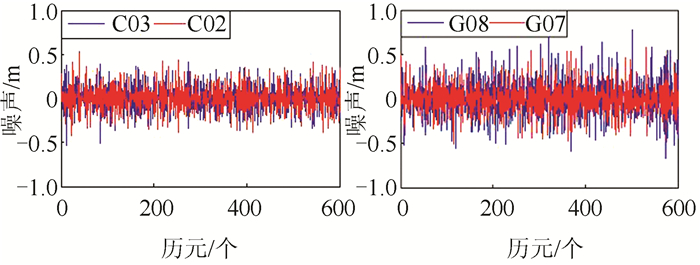 |
| 图 8 BDS/GPS P2码观测值噪声序列 Fig.8 BDS/GPS P2 Code Observed Noise Sequence |
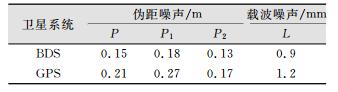
| 表 3 R9伪距与载波噪声RMS统计表 Tab.3 R9 Pseudorange and Carrier Noise RMS Statistics Table |
 |
由图 5、图 6可以看出,BDS系统的相位噪声、码噪声小于GPS系统,究其原因是因为C02、C03为GEO卫星,处于连续跟踪状态,卫星高度角较大所致。BDS与GPS系统内的两个卫星噪声水平相当,说明通道间相位观测值噪声无明显差异,BDS与GPS在这一点上具有一致性。
由图 7、图 8可以看出,BDS与GPS基本处于同一水平,且P1码噪声大于P2码噪声。与图 6对比可知,利用第一种模型求得的混合P码噪声大于第二种模型求得的P2码噪声,小于第二种模型求得的P1码噪声。
与表 2对比可得,单站检测法检测的噪声略大于零基线检测法检测的噪声。
3 结束语单站检测法检测的是接收机的系统噪声,包含接收机内部噪声、天线以及与之相连的电缆的噪声,还有因环境因素造成的噪声,甚至还有卫星发射信号时带来的噪声,它是各种噪声的综合。零基线双差法检测的噪声小于单站检测法检测的噪声。BDS与GPS码噪声基本处于同一水平,BDS相位噪声小于GPS相位噪声。对于伪距而言, P2码噪声小于P1码噪声;对于载波而言,L1载波噪声与L2载波噪声无明显差别,且BDS与GPS系统具有一致性。
就检测效果而言,两两配对进行零基线检验,可以判断出质量较差的接收机;根据噪声水平的经验值,利用单站检测法检测出质量较差的接收机。在进行接收机检测时应当结合实际情况选取合适的方法,或者同时使用两种方法,对接收机的噪声进行全面的评价。
| [1] |
蔡昌盛. 多模GNSS融合精密单点定位理论与方法[M]. 北京: 科学出版社, 2017.
|
| [2] |
胡玉坤. GNSS观测值质量评估与接收机噪声检测[D].北京: 中国科学院大学, 2016
|
| [3] |
刘俊宏, 鞠冰, 赖育网, 等. 北斗接收机观测数据质量评估[J]. 第四届中国卫星导航学术年会, 武汉, 2013. |
| [4] |
潘林, 蔡昌盛, 戴吾蛟, 等. 北斗与GPS数据质量对比分析[J]. 全球定位系统, 2013, 38(2): 23-26. DOI:10.3969/j.issn.1008-9268.2013.02.005 |
| [5] |
谭羽安, 袁本银, 鲍志雄. GPS/BD/GLONASS多星座质量检核研究与实现[C].第四届中国卫星导航学术年会, 武汉, 2013 http://cpfd.cnki.com.cn/Article/CPFDTOTAL-WXDH201305006019.htm
|
| [6] |
刘荟萃, 唐歌实, 崔红正, 等. 多模GNSS数据质量检测方法与软件研发[J]. 测绘与空间地理信息, 2014, 37(1): 5-8. DOI:10.3969/j.issn.1672-5867.2014.01.003 |
| [7] |
戴水财, 朱建军, 张学庄, 等. GPS接收机内噪声水平的评价与检测方法[J]. 北京测绘, 2007(1): 14-18. DOI:10.3969/j.issn.1007-3000.2007.01.004 |
| [8] |
高晓, 戴吾蛟, 李施佳. 高精度GPS/BDS兼容接收机内部噪声检测方法研究[J]. 武汉大学学报·信息科学版, 2015, 40(6): 795-799. |
| [9] |
Resch G M, Jacobs C, Keihm S, et al. Calibration of Atmospherically Induced Delay Fluctuations due to Water Vapor[C]. International VLBI Service for Geodesy and Astrometry 2000 General Meeting Proceedings, K tzting, Germany, 2000 https://www.researchgate.net/publication/23891933_Calibration_of_Atmospherically_Induced_Delay_Fluctuations_Due_to_Water_Vapor
|
| [10] |
Braasch M S. Isolation of GPS Multipath and Receiver Tracking Errors[J]. Navigation, 1994, 41(4): 415-435. DOI:10.1002/navi.1994.41.issue-4 |
| [11] |
毛刚, 莫钧. 高精度BD2/GPS兼容接收机性能测试与分析[J]. 第一届中国卫星导航学术年会, 北京, 2010. |
| [12] |
游振东. GNSS接收机内部性能检测方法的研究[D].武汉: 武汉大学, 2005 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y742781
|
 2019, Vol. 44
2019, Vol. 44

