| 神经网络在甚短弧初轨确定问题中的应用 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
随着各国航天活动的不断增加,大量的空间碎片产生,形成了危害性巨大的空间碎片环境[1]。低轨空间碎片的运行速度很快,其与地基观测平台的平均相对速度一般可达到7.8 km/s,与天基观测平台的平均相对速度则能够达到10 km/s[2]。因此,大多数情况下只能得到较短的观测角度序列。根据单个弧段的有限观测信息进行初始轨道确定,得到一组粗略的轨道根数,即甚短弧初轨确定问题[3]。
将传统的Gauss方法和Gooding方法应用于甚短弧初轨确定时,由于观测数据稀疏,会出现迭代不收敛或者平凡解等现象,很难得到好的定轨结果[3, 4]。而其他基于光学观测数据的初轨确定技术又存在解算成功率不高或解算精度不高的问题[3-9]。近些年来,有学者将神经网络技术应用于低轨卫星轨道预报中,取得了不错的结果[10],但是未见该算法在初轨确定中的应用。基于此,本文提出使用神经网络算法来提升传统的初轨解算方法的精度。
1 深度学习与初轨确定神经网络的“万能近似”定理给出,只要神经网络中拥有足够多的隐藏单元和足够合适的激活函数,它就可以以任意的精度来近似任何一个从有限维空间到另一个有限维空间的Borel可测函数[11]。其原理可以用图 1表示。
 |
| 图 1 神经网络的原理示意图 Fig.1 Schematic Diagram of Neural Network |
图 1中,f表示从一个有限维空间到另一个有限维空间的Borel可测函数,Σ表示该可测函数f的输入,f (Σ)表示该可测函数f的输出。神经网络的作用即是通过足够多的神经元以组成一个足够合适的神经网络结构(用θ来表示构建神经网络模型时所用到的参数)来近似可测函数f(近似的函数结果用
在基于仅角度观测值的甚短弧初始轨道确定的问题中,用Σi表示一组地基角度观测值,RAij、Decij分别表示这组观测值中某一时刻j空间目标相对于地基光学观测设备中心的赤经、赤纬,那么角度观测值如下:
| $ \mathit{\pmb{\Sigma}}_i=\left[\begin{array}{cc} R A_{i 1} & \operatorname{Dec}_{i 1} \\ R A_{i 2} & \operatorname{Dec}_{i 2} \\ \vdots & \vdots \\ R A_{i n} & \operatorname{Dec}_{i n} \end{array}\right] $ | (1) |
式中,n表示第i组观测值中的总观测次数。
同时,用σi表示某组角度观测量Σi所对应的空间目标某时刻的真实轨道根数解,形式为:
| $ \boldsymbol{\sigma}_i=\left[a_i, e_i, i_i, \mathit{\Omega}_i, \omega_i, M_i\right]^{\mathrm{T}} $ | (2) |
式中,a、e、i、Ω、ω、M分别表示轨道六根数中的长半径、偏心率、轨道倾角、升交点赤经、近地点幅角和平近点角。
甚短弧初轨确定问题可以看作是求解一组角度观测值和与之对应的真实轨道根数解之间的精确数学方程问题。可以将角度观测值Σi看作数学方程的输入,真实轨道根数解σi看作数学方程的输出,那么该问题就是一个由观测值Σi所组成的有限维输入空间到一个由真实轨道根数解σi所组成的有限维输出空间之间的Borel可测函数问题。
显然,只要有足够合适的神经网络模型就可以以任意精度来描述甚短弧初轨确定问题。基于此,本文将神经网络应用于甚短弧初轨确定问题中,程序框图如图 2所示。
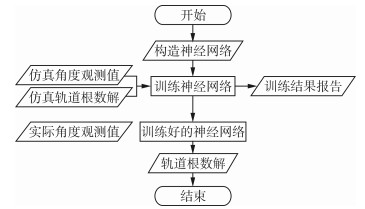 |
| 图 2 甚短弧初轨确定程序框图 Fig.2 The Program Diagram of the very Short Arc Initial Orbit Determination |
需要说明的是,该算法有一个基本假定,即给定一组甚短弧观测数据,已用某种方法解算获得了一组粗略的轨道根数;在此基础上,利用本文的神经网络算法,改进轨道根数的解算精度。
2 实验设计方案 2.1 输入/输出数据生成首先假设观测站的坐标已知,记为:
| $ \operatorname{obv}_{\mathrm{CGCS2000}}=\left[\begin{array}{lll} B & L & H \end{array}\right]^{\mathrm{T}} $ | (3) |
式中,B、L、H分别表示测站的大地纬度、大地经度和大地高。
其次,利用武汉大学空间目标轨道信息软件平台[12],并联合多个两行根数(two lines element, TLE)进行精密轨道预报,可以得到10 d内最大预报误差小于5 km的“真轨道”[13]。
取某一“真轨道”观测时间段ti1~tin内的天球惯性坐标系的位置矢量,记为
| $ \mathrm{obj}_{\mathrm{CIS}}^{t_{ij}}=\left[\begin{array}{lll} X_{\mathrm{CIS}}^{t_{ij}} & Y_{\mathrm{CIS}}^{t_{ij}} & Z_{\mathrm{CIS}}^{t_{ij}} \end{array}\right]^{\mathrm{T}} $ | (4) |
将观测站的大地坐标转换成地固坐标系下的坐标:
| $ \mathrm{obv}_{\mathrm{CTS}}=\left[\begin{array}{l} x_{\mathrm{obv}} \\ y_{\mathrm{obv}} \\ z_{\mathrm{obv}} \end{array}\right]=\left[\begin{array}{c} (N+H) \cos B \cos L \\ (N+H) \cos B \sin L \\ \left(N\left(1-e^2\right)+H\right) \sin B \end{array}\right] $ | (5) |
式中,N表示测站点卯酉圈半径;e是CGCS2000地球椭球参数中的第一偏心率。
再将观测站的地固坐标转换成天球惯性坐标:
| $ \mathrm{obv}_{\mathrm{CIS}}^{t_{ij}}=\left[\begin{array}{c} X_{\mathrm{obv}}^{t_{ij}} \\ Y_{\mathrm{obv}}^{t_{{ij}}} \\ Z_{\mathrm{obv}}^{t_{ij}} \end{array}\right]=\mathit{\boldsymbol{RM}}^{t_{i j}}\left[\begin{array}{l} x_{\mathrm{obv}} \\ y_{\mathrm{obv}} \\ z_{\mathrm{obv}} \end{array}\right] $ | (6) |
| $ \mathit{\boldsymbol{R M}}^{t_{i j}}=\left(\mathit{\boldsymbol{E P}}^{t_{i j}}\right)\left(\mathit{\boldsymbol{E R}}^{t_{i j}}\right)\left(\mathit{\boldsymbol{N R}}^{t_{i j}}\right)\left(\mathit{\boldsymbol{P R}}^{t_{i j}}\right) $ | (7) |
式中,RM为旋转矩阵;EP为极移矩阵;ER为地球旋转矩阵;NR为章动矩阵;PR为岁差矩阵。
由式(4)和式(6),可以计算出每个时刻ti空间目标相对于观测站的赤经和赤纬:
| $ R A_{t_{i j}}=\tan ^{-1} \frac{\Delta X_{t_{i j}}}{\Delta Y_{t_{i j}}} $ | (8) |
| $ \operatorname{Dec}_{t_{i j}}=\tan ^{-1} \frac{\Delta Z_{t_{i j}}}{\sqrt{\Delta X_{t_{i j}}{ }^2+\Delta Y_{t_{i j}}{ }^2}} $ | (9) |
其中,∆Xtij、∆Ytij、∆Ztij的计算公式分别为:
| $ \Delta X_{t_{ij}}=X_{\mathrm{CIS}}^{t_{ij}}-X_{\mathrm{obv}}^{t_{ij}} $ | (10) |
| $ \Delta Y_{t_{i j}}=Y_{\mathrm{CIS}}^{t_{i j}}-Y_{\mathrm{obv}}^{t_{i j}} $ | (11) |
| $ \Delta Z_{t_{ij}}=Z_{\mathrm{ClS}}^{t_{ij}}-Z_{\mathrm{obv}}^{t_{ij}} $ | (12) |
实验中假设赤经赤纬的观测误差都为10″的高斯误差。
2.2 实验方案本文选取了在2017年11月10日—11日期间,某假设地基测站(见表 1)根据“真轨道”所捕捉到的50个低轨TLE(long term evolution)目标。
| 表 1 假设的地基观测站信息 Tab.1 Assumed Ground Station Information |
 |
同时,在每个目标的起始轨道根数周围根据不同的高斯误差分布(见表 2),仿真生成了2 000组起始轨道根数。并采用精确的力学模型(Cowell积分器,并使用60×60 JGM-3重力场、日月引力、地球固体潮和海潮以及DTM78大气密度模型等轨道力学模型)产生其对应的仿真轨道。
| 表 2 各仿真实验的轨道根数高斯分布标准差 Tab.2 STD of Orbit Elements in Simulation Experiments |
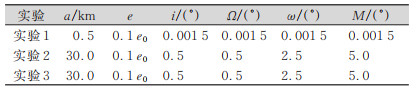 |
为展示本文方法的适用性,本文设计了3个实验,每个实验中均含该50个低轨空间目标。假定通过某种方法已获得了每个目标的一组粗略轨道根数,其误差如表 2所示。第1个实验中的粗略轨道根数误差很小,其目的主要是对算法进行验证和测试。第2和第3个实验中假定长半径误差为30 km,偏心率误差为10%,倾角i和升交点赤经Ω误差为0.5°,近地点幅角ω和平近点角M的误差分别为2.5°和5.0°,它们可用于代表某种初轨的确定方法(例如文献[2]的距离搜索法)解算的粗略初轨根数的误差。
给定某个目标的一组轨道根数,首先确定该目标相对于测站的可见性,如果可见,则利用式(3)~式(12),就可以计算该空间目标相对于测站的一组角度观测值。只选取可见弧段最初的21 s,因此,测角数据的弧长只有21 s。同时,在计算的角度值中添加10″的随机误差。实验1和实验2假定角度观测频率为1 Hz,实验3为1/3 Hz。因此,实验3对应于甚短弧和稀疏数据两者共存的情况。每个弧段的观测数据信息见表 3。
| 表 3 各仿真实验的观测弧段信息 Tab.3 The Arc Information of Each Simulation Experiment |
 |
为了进行神经网络的训练和验证,对每个目标均生成2 000组轨道根数及其对应的仿真观测数据。然后,将2 000组数据随机分成两部分,其中1 500组数据作为神经网络的训练样本对神经网络进行训练,另外500组作为验证集,用于对神经网络的计算结果进行分析与评定。
利用Python的Scikit-Learn库中的主成分分析算法(principal component analysis, PCA)和Keras库的全连接神经网络函数来对实验数据进行处理。设计主成分分析的目标维数为20维,神经网络包括3层全连接层,每层包含200个神经元,使用Re Lu函数作为激活函数,同时设计神经网络的评价函数为平均绝对误差(mean absolute error, MAE),最大迭代次数为200次。
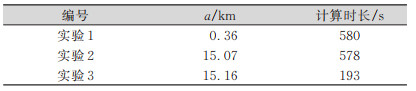
3 实验结果根据上述方案进行实验,结果如表 4所示。对于甚短弧初轨确定问题,长半径是最难于确定的根数,因此,仅给出长半径的均方误差,同时给出3个仿真实验的计算时长。
| 表 4 长半径均方误差及计算时长统计表 Tab.4 Semi-major Axis MSE of Verification Set and Calculation Duration |
 |
各仿真实验验证集中空间目标的长半轴均方误差分布如图 3所示。
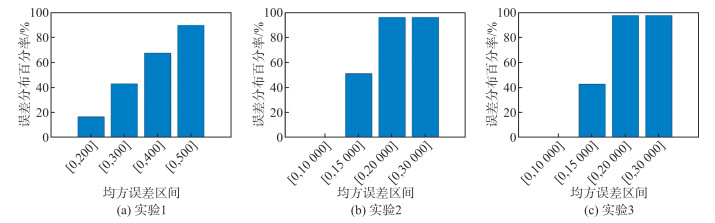 |
| 图 3 长半径验证集均方误差分布 Fig.3 MSE Distribution of Semi-major Axis |
由表 4可以看出,当实验1中粗略轨道长半径的误差均方根为500 m时,通过神经网络训练,其值减小了28%。对于实验2和实验3,粗略轨道长半径的误差均方根为30 km时,通过神经网络训练,其值减小了约50%,表明算法对提升长半径精度具有明显的效果。并且从图 3中可以看出,约98%的目标的最终解算精度都能够优于20 km。实验3中的测角频率仅为1/3 Hz,但最终长半径的误差均方根与实验2基本相同,表明角度数据的稀疏性对神经网络算法的解算提升效果基本没有影响。同时,也可以看出仿真实验的计算效率与输入的弧段稀疏程度成相关关系,弧段越稀疏,其计算效率会相对提高。
4 结束语甚短弧初轨确定即是在没有任何初始信息的前提下,利用较短弧段的观测数据,采用比较简单的动力学模型(通常是二体模型)快速计算出空间目标的粗略初始轨道[14]。传统的初轨确定算法应用于仅角度观测值的甚短弧初轨确定问题时,会出现迭代不收敛或者平凡解等现象,很难得到好的定轨结果。
本文开展了前馈神经网络应用于提升甚短弧初轨确定精度的仿真实验研究。实验结果表明,假定通过某种方法获得了一组粗略轨道根数,神经网络算法能够提升初轨长半径的确定精度。当长半径均方根误差为500 m时,提升幅度为28%;当长半径均方根误差为30 km时,提升幅度约为50%左右。而且,测角频率从1 Hz降至1/3 Hz时,对提升幅度基本没有影响。
尽管本文中的仿真实验场景与真实观测场景可能存在一定差异,但只要在神经网络算法中仔细考虑有关差异,构造合适的神经网络模型,该算法是可以应用于提升其他甚短弧初轨确定算法的解算精度的,并有望获得更高精度的轨道参数解。下一步,我们将考虑更多的轨道类型、弧段长度、数据频率等因素,分析本文方法适用性的条件,开展实测数据的算法性能分析。
| [1] |
空间碎片环境现状与主动移除技术[J]. 航天器环境工程, 2014, 31(2): 129-135. |
| [2] |
空间碎片监测移除前沿技术与系统发展[J]. 科学通报, 2018, 63(25): 2570-2591. |
| [3] |
一种天基测向初轨确定方法[J]. 国防科技大学学报, 2009, 31(1): 11-15. |
| [4] |
应用距离搜索的低轨空间碎片初始轨道确定方法[J]. 航天器工程, 2017, 26(2): 22-28. |
| [5] |
Gooding R H. A New Procedure for Orbit Determination Based on Three Lines of Sight(Angles Only)[R]. Defence Research Agency Farnborough(United Kingdom), 1993.
|
| [6] |
Gooding R H. A New Procedure for the Solution of the Classical Problem of Minimal Orbit Determination from Three Lines of Sight[J]. Celestial Mechanics and Dynamical Astronomy, 1996, 66(4): 387-423. |
| [7] |
Vallado D A. Evaluating Gooding Angles-Only Orbit Determination if Space Based Space Surveillance Measurements[J]. Paper USR, 2010, 10-14. |
| [8] |
一种基于星间方向观测的初轨计算方法[J]. 宇航学报, 2007(3): 619-622. |
| [9] |
LEO空间目标地基甚短弧角度数据初轨确定[J]. 测绘地理信息, 2019, 44(2): 71-73. |
| [10] |
杨先睿. 基于深度学习的卫星轨道预报算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [11] |
Goodfellow I, Beigio Y, Courville A. 深度学习[M]. 赵申剑, 黎彧君, 符天凡, 译. 北京: 人民邮电出版社, 2017.
|
| [12] |
空间目标轨道信息软件平台的建设[J]. 航天器环境工程, 2016, 33(1): 1-6. |
| [13] |
联合多个两行根数进行轨道预报[J]. 红外与激光工程, 2016, 45(S2): 35-39. |
| [14] |
关于各种类型数据的初轨计算方法[J]. 飞行器测控学, 2009, 28(3): 70-76. |
 2022, Vol. 47
2022, Vol. 47


