北斗卫星导航系统(BeiDou navigation satellite system，BDS)是中国正在实施的自主发展、独立运行的全球卫星导航系统^[1]。BDS卫星可发射3个频率的信号(B₁=1 561.098 MHz，B₂=1 207.140 MHz，B₃=1 268.520 MHz)^[2]。根据北斗系统公开服务性能规范公布了北斗系统服务区内公开服务定位、测速和授时的精度指标。其中，北斗的测速精度指标为0.2 m/s (95%置信度)^[3]。

国内外一些学者对BDS的测速原理和测速精度进行了相关分析^[4-6]，并对多种测速方法进行了比较^[7]。本文通过对实测数据处理，分别对利用BDS各个频点的多普勒观测值进行测速的精度进行了分析。

1 多普勒频移

由于接收机和卫星之间的相对运动，使得接收机接收到的信号频率f_r不再是卫星信号的发射频率f，而是f+f_d。将这种信号接收频率f_r随信号发射源与接收机之间的相对运动而发生变化的现象称为多普勒效应，而将f_d称作多普勒频移^[8]。这样多普勒频移等于信号接收频率与信号发射频率f之间的差异，即

$ {{f}_{d}}={{f}_{r}}-f $

(1)

设卫星s的运动速度为v^s，发射频率为f，波长为λ，接收机的速度为v。接收机接收到的卫星载波信号的多普勒频移为：

$ {{f}_{d}}=\frac{(\mathit{\boldsymbol{v}}-{{\mathit{\boldsymbol{v}}^{s}})}{\mathit{\boldsymbol{I}}}}{\lambda }=-\frac{({{\mathit{\boldsymbol{v}}}^{s}}-\mathit{\boldsymbol{v}}){\mathit{\boldsymbol{I}}}}{\lambda }=-\frac{{\dot{r}}}{\lambda } $

(2)

式中，I是卫星在接收机处的单位观测向量，该向量与接收机相对于卫星的运行速度(v－v^s)的内积就等于接收机向卫星靠近的距离变化率- $ \dot{r} $，其中$ \dot{r} $代表卫星与接收机之间的几何距离r对时间的导数。

在BDS多普勒观测中，接收机内部通过频率锁定环路(FLL)不断地调整复制一个包含多普勒频移在内的某一载波频率，使其与接收到的卫星信号的载波频率尽量一致，然后输出多普勒频移测量值f_d^[9]：

$ \lambda \times {{f}_{d}}=\dot{P} $

(3)

其中，$ \dot{P} $为伪距变化率，含有卫星和接收机的相对速度分量，如果将卫星运行速度v^s所引起的多普勒频移从f_d中扣除，剩余部分的多普勒频移反映的是接收机的运行速度v，卫星的速度可以通过广播计算得到。BDS的空间卫星星座分为GEO、IGSO和MEO三种，IGSO和MEO卫星速度的计算方法与GPS卫星一致^[9]，而GEO卫星的位置、速度和计算方法略有不同^[10]，要分开考虑。

2 BDS单点测速原理

在协议地球坐标系中，某一历元测站r对卫星s的伪距观测值可表示为：

$ \begin{align} &P_{r}^{s}=\sqrt{{{({{X}^{s}}-{{X}_{r}})}^{2}}\text{+}{{({{Y}^{s}}-{{Y}_{r}})}^{2}}\text{+}{{({{Z}^{s}}-{{Z}_{r}})}^{2}}} \\ &+c{\rm{d}}{{t}_{r}}-c{\rm{d}}{{t}^{s}}+I_{r}^{s}+T_{r}^{s}+\varepsilon \\ \end{align} $

(4)

式中，P_r^s为伪距观测值；(X_r, Y_r, Z_r)和(X^s, Y^s, Z^s)分别表示测站r和卫星s的空间直角坐标；c为光速；dt_r和dt^s分别为接收机钟和卫星钟差；I_r^s为电离层延迟改正；T_r^s为对流层延迟改正；ε表示伪距的观测噪声和多路径延迟的影响。

对式(4)进行时间微分可得：

$ \dot{P}_{r}^{s}=\left[ \begin{matrix} \begin{align} &-l_{r}^{s} \\ &-m_{r}^{s} \\ &-n_{r}^{s} \\ &\;\;\;1 \\ \end{align}\\ \end{matrix} \right]\left[ \begin{matrix} \dot{X}-{{{\dot{X}}}^{s}} \\ \dot{Y}-{{{\dot{Y}}}^{s}} \\ \dot{Z}-{{{\dot{Z}}}^{s}} \\ c{\rm{d}}{{{\dot{t}}}_{r}} \\ \end{matrix} \right]-c{\rm{d}}{{\dot{t}}^{s}}+\dot{I}_{r}^{s}+\dot{T}_{r}^{s} $

(5)

式中，$ l_{r}^{s}=({{X}^{s}}-{{X}_{0}})/\rho _{0}^{s}、m_{r}^{s}=({{Y}^{s}}-{{Y}_{0}})/\rho _{0}^{s}、n_{r}^{s}=({{Z}^{s}}-{{Z}_{0}})/\rho _{0}^{s} $为从接收机r位置到卫星s方向上的方向余弦, $ \rho _{0}^{s}=\sqrt{{{({{X}^{s}}-{{X}_{r}})}^{2}}\text{+}{{({{Y}^{s}}-{{Y}_{r}})}^{2}}\text{+}{{({{Z}^{s}}-{{Z}_{r}})}^{2}}} $表示通过接收机初值坐标计算的几何距离初值。

为了便于列误差方程，可将式(5)改写为：

$ \begin{array}{l} \lambda D_r^s = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} - l_r^s\\ - m_r^s\\ - n_r^s\\ \;\;\;1 \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot X}_r}}\\ {{{\dot Y}_r}}\\ {{{\dot Z}_r}}\\ {c{\rm{d}}{{\dot t}_r}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} \begin{array}{l} - l_r^s\\ - m_r^s\\ - n_r^s \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot X}^s}}\\ {{{\dot Y}^s}}\\ {{{\dot Z}^s}} \end{array}} \right] - \\ c{\rm{d}}{{\dot t}^s} + \dot I_r^s + \dot T_r^s \end{array} $

(6)

式中，D_r^s为多普勒频移观测量；($ {{\dot{X}}_{r}}, \dot{Y}, {{\dot{Z}}_{r}} $)为测站三维空间速度；($)为卫星三维空间速度；$ {\rm{d}}{{\dot{t}}_{r}} $为接收机钟差变化率；$ {\rm{d}}{{\dot{t}}^{s}} $为卫星钟差变化率；$ \dot{I}_{r}^{s} $和$ \dot{T}_{r}^{s} $分别为电离层和对流层变化率。卫星速度可以在导航电文中获得。

在BDS多普勒测速中，主要误差包括卫星位置误差、卫星速度误差、卫星钟速度误差、接收机位置误差和大气延迟变化误差等。其中，大气延迟变化误差在短时间可以忽略不计；卫星位置误差和接收机位置误差对多普勒测速的影响原因类似，其对测速的误差优于1 mm/s，可以忽略^[5]；卫星速度误差、卫星钟速度误差亦可忽略不计。故BDS多普勒单点测速的误差主要由多普勒观测值的精度引起，在可用卫星数大于4颗的情况下，可以通过最小二乘原理解算接收机的三维空间速度和钟差速度。

因此，对于不同频率的多普勒观测值，式(6)中的与频率有关项的只有多普勒观测值λD_r^s。

3 算例分析 3.1 试验数据描述

本文主要分析北斗B₁、B₂和B₃等3个频率的多普勒观测值的精度。试验采用静态实测数据分析。实测数据采用武汉地区的Trimble NetR9接收机和浙江的攀达时空PD318型接收机，采样率为1 Hz，采样时间为1 h，共3 600个历元。这两款接收机均能接收北斗B₁、B₂和B₃等3个频率的导航信息，并输出原始观测数据。

3.2 多普勒测速精度分析

利用C++编写多普勒测速程序，分别处理天宝NetR9和攀达PD318型接收机的B₁、B₂和B₃等3个频点的多普勒观测数据，并进行误差分析。由于试验接收机是静态的，故接收机的速度真值应为0，解算出的速度值可认为是速度解算的真误差。

图 1和图 2分别给出了天宝NetR9和攀达PD318的B₁、B₂和B₃频率多普勒测速结果。

从图 1可以看出，天宝NetR9在B₂和B₃频率的多普勒测速精度明显优于B₁频率的多普勒测速精度，这种现象存在两种可能性：①B₂和B₃的多普勒观测值精度比B₁频率高; ②Trimble NetR9接收机输出的B₁多普勒观测值为原始多普勒观测值，而B₂和B₃为导出多普勒观测值。通过对比多普勒观测值和载波相位观测值，得出第二种可能是正确的，即Trimble NetR9的B₂和B₃多普勒观测值为导出多普勒观测值。导出多普勒观测值的计算公式如下^[6]：

$ \bar{D}_{r}^{s}=\frac{{{\varphi }_{k+1}}-{{\varphi }_{k}}}{{{t}_{k+1}}-{{t}_{k}}} $

(7)

由式(7)并结合误差传播率可知，在采样率为1 Hz时，导出多普勒观测值的精度为载波相位的$ \sqrt{2} $倍。

从图 2可以看出，攀达PD318在B₂和B₃频率的多普勒测速精度略优于B₁频率，同样采用对比多普勒观测值和载波相位观测值的方法，认为攀达PD318输出的B₂和B₃多普勒观测值为原始多普勒观测值。结合图 1和图 2可以看出，天宝NetR9的测速精度要优于PD318。统计这两款接收机多普勒测速结果，得到其均方根误差RMS，如表 1所示。

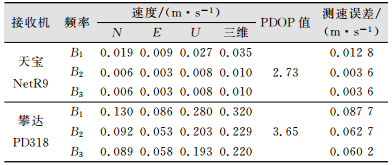从表 1可以看出，天宝NetR9的多普勒测速精度为cm/s，攀达PD318的多普勒测速精度为dm/s，NetR9较PD318高出一个数量级，可以看出接收机对多普勒测速的影响是十分巨大的。

4 结束语

1) 在本试验中，攀达PD318接收机的B₁、B₂和B₃多普勒测速精度分别为0.320 m/s、0.229 m/s、0.220 m/s，北斗3个频率的多普勒测速的精度可达dm/s；天宝NetR9接收机的的B₁、B₂和B₃多普勒测速精度分别为0.035 m/s、0.010 m/s、0.010 m/s，北斗3个频率的多普勒测速的精度可达cm/s。

2) 攀达PD318接收机B₁频率的多普勒观测值精度为0.087 m/s；北斗B₂和B₃原始多普勒观测值的精度比B₁分别高出28.4%和31.3%。天宝NetR9接收机B₁的多普勒观测值精度为0.013 m/s；天宝NetR9输出的B₂和B₃导出多普勒观测值精度比B₁高71.4%。