| 基于稳健总体最小二乘的GPS水准拟合研究 |
2. 核工业建设集团有限公司, 江苏 南京, 210000;
3. 辽宁工程技术大学测绘与地理科学学院, 辽宁 阜新, 123000
2. The Nuclear Industry Construction Group Limited Company, Nanjing 210000, China;
3. School of Mapping and Geographical Science, Liaoning Technical University, Fuxin 123000, China
在利用最小二乘(least squares,LS)法估计未知参数时,通常默认观测值不含系统误差或粗差,所得参数解是最优无偏解。在实际参数估计过程中,误差方程的系数矩阵(包括线性方程或经过泰勒展开的非线性方程,如全球定位系统(global positioning system,GPS)观测方程、变形位移方程等)本身就会包含误差,这些误差不仅与控制点的数量、观测值类型和观测网形有关,而且还与待定点的近似值等内容有关[1, 2]。虽然LS是测量数据处理时最常用且最重要的方法,但该方法仅考虑了观测误差是偶然误差的情况;而总体最小二乘(total least squares,TLS)在参数求解的过程中同时考虑了系数矩阵和观测向量存在误差的情况。因此它是顾及各种观测量随机误差的一种最优算法[3]。国内外学者对TLS在测量领域的应用展开了一系列研究,如直线拟合[4, 5]、平面拟合[6]、水准测量[7]、坐标转换[8]、地壳应变参数反演[9]等。
GPS水准拟合一般通过建立平面坐标与高程异常之间的多项式函数实现,该方法的基本原理是将平面坐标作为自变量,采用LS拟合多项式,该方法可以满足目前大部分的工程需求,然而经典的高斯-马尔科夫模型不能有效地应对系数矩阵中存在的误差。因此,针对GPS水准拟合中观测数据存在粗差和系数矩阵存在误差的情况,尝试采用一种顾及加权稳健总体最小二乘(robust total least squares,RTLS)迭代算法拟合多项式函数,利用实验数据分析了LS与总体最小二乘奇异值(singular value decomposition-total least squares,SVD-TLS)法、混合最小二乘(mixed total least squares,MTLS)法的差异性。以某市实测GPS高程数据为例,将利用抗差LS拟合的高程异常值作为参考值,分析SVD-TLS、MTLS和RTLS在GPS水准拟合中效果,验证RTLS在GPS水准拟合中的可行性和有效性。
1 基于不同算法的总体最小二乘 1.1 总体最小二乘奇异值法矩阵的奇异值分解是解决线性代数问题的工具之一,该分解法应用于统计学、矩阵的求逆、信号与图像处理以及在误差平差中的整体最小二乘、最小二乘、优化的问题中,设误差方程为:
| $\left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\mathit{\boldsymbol{B}}}} \right)\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{L}} + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\mathit{\boldsymbol{L}}} $ | (1) |
式中,Ln×1为观测向量;Bm×n为系数矩阵;Xm×1为未知参数;ΔB和ΔL分别为系数矩阵和观测向量中存的随机误差矩阵;B∈Rm×n, L∈Rm, x∈Rn, m>n, r(B)=n,其平差准则为[10]:
| $\min :\mathit{S} = {\left\| {\mathit{\boldsymbol{D}}\left[ {{\mathit{\boldsymbol{E}}_\mathit{\boldsymbol{B}}},e} \right]\mathit{\boldsymbol{T}}} \right\|_F} $ | (2) |
式中,D=diag(d1, …, dn)和T=diag(t1, …, tm+1)为权对角阵,且di和ti均为正常数。
SVD-TLS通过分解增广矩阵进而求解参数,能较好地处理病态矩阵,是求解TLS最常用、最严密有效的方法,不过缺少平差模型统计意义上的最佳估值,所以它的适用范围具有一定的局限性。
1.2 混合总体最小二乘法在求解参数过程中,可以将LS和TLS混合使用,称为混合整体最小二乘,设误差方程为:
| $\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}} \end{array}} \right] = \mathit{\boldsymbol{L}} $ | (3) |
式中,B=[B1 B2], B1∈Rm×n1, B2∈Rm×n2;x=[x1T x2T]T, x1∈Rn1, x2∈Rn2, n=n1+n2。其中,B1是系数矩阵B中没有误差的部分;m是观测值个数;n是待估参数的个数;n1、n2分别为B1、B2对应的参数个数。混合TLS矩阵分解法平差准则为[11]:
| $\mathop {\min }\limits_{\left[ {{{\mathit{\boldsymbol{\hat B}}}_2};\mathit{\boldsymbol{\hat L}}} \right] \in {\mathit{\boldsymbol{R}}_{m \times \left( {{n_2} + 1} \right)}}} {\left\| {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_2}}&\mathit{\boldsymbol{L}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat B}}}_2}}&{\mathit{\boldsymbol{\hat L}}} \end{array}} \right]} \right\|_F} $ | (4) |
| $\mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{\hat L}}} \right) \subseteq \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{\hat B}}} \right) = \mathit{\boldsymbol{R}}\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}&{{{\mathit{\boldsymbol{\hat B}}}_2}} \end{array}} \right]} \right) $ | (5) |
在该准则下,寻求
SVD-TLS是从矩阵的特征值与零空间的角度出发拟合方程,而TLS迭代法一般是从测量平差角度出发,借助拉格朗日极值法并依据一定准则拟合方程。结合测量平差的优势,汪奇生等根据线性回归模型的特点推导出一种新的TLS迭代算法[12, 13]。设线性回归模型为:
| $y = {\hat a_0} + {\hat a_1}{x_1} + {\hat a_2}{x_2} + \cdots + {\hat a_n}{x_n} $ | (6) |
考虑SVD-TLS默认系数矩阵中不含误差的列向量也含有误差,为了方便地处理系数矩阵中含有误差部分,将式(6)进行变形为:
| ${\hat b_0}y + {\hat b_1}{x_1} + {\hat b_2}{x_2} + \cdots + {\hat b_n}{x_n} = 1 $ | (7) |
式中,
| $\left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{E}}_B}} \right)\hat x + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{X}}^0} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}^0} - \mathit{\boldsymbol{W}} = 0 $ | (8) |
式中,EX0=FV; BX0=FL; L=vec(B); 式(8)中
| $\left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{E}}_B}} \right)\hat x + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{X}}^0} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}^0} - \mathit{\boldsymbol{W}} = 0 $ | (9) |
式中,V=vec(EB); Q是观测值的协因数阵。根据拉格朗日极值求解出线性回归方程的TLS解为:
| $\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} \mathit{k}\\ {\mathit{\hat x}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{FQ}}{\mathit{\boldsymbol{F}}^\mathit{\rm{T}}}}&{\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}}}\\ {{{\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}}} \right)}^{\rm{T}}}}&{\rm{0}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} - \mathit{\boldsymbol{FL}}}\\ {\rm{0}} \end{array}} \right]\\ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{K}} \end{array} \right. $ | (10) |
在线性回归方程中,假设坐标与高程异常为等精度观测值,在迭代初始,可设Q为单位阵,但在二次曲面多项式中,系数矩阵的列向量之间是非线性关系,根据误差传播定律可得,Qxi2=4xi2Qxi,Qxiyi=(xi2+yi2)Qxi,Qyi2=4yi2Qyi。假设线性无关的列向量等权,因此二次曲面拟合的初始协因数阵的表现形式为:
| ${\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{B}}} = {\mathit{\boldsymbol{Q}}_0} \otimes {\mathit{\boldsymbol{Q}}_\mathit{y}} $ | (11) |
Q0为行向量协因数阵,为计算方便简化Q0,
| $P_{L(t)}^{i + 1} = \left\{ {\begin{array}{*{20}{l}} {1,\;\;\left| {{V_{y(t)}}} \right| \le 2{{\hat \sigma }_0}}\\ {2{{\hat \sigma }_0}/\left| {{V_{y(t)}}} \right|,\;\;\;\left| {{V_{y(t)}}} \right| > 2{{\hat \sigma }_0}} \end{array}} \right. $ | (12) |
式中,i为迭代次数;
1) 根据式(1),利用TLS求解回归参数估值
2) 假设E0=0,根据一次拟合或者二次拟合选择对应初始单位权阵。根据式(10),利用初值X(0)计算参数改正数
| $\left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}^{0\left( {i + 1} \right)}} = {\mathit{\boldsymbol{X}}^{0\left( i \right)}} + {{\hat x}^{\left( {i + 1} \right)}}\\ {\mathit{\boldsymbol{V}}^{\left( {i + 1} \right)}} = {\mathit{\boldsymbol{Q}}^0}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{K}}\\ {\mathit{\boldsymbol{E}}^{\left( {i + 1} \right)}} = {\rm{ve}}{{\rm{c}}^{ - 1}}\left( {{\mathit{\boldsymbol{V}}^{\left( {i + 1} \right)}}} \right) \end{array} \right. $ | (13) |
3) 重复步骤2),直到|X0(i+1)-X0(i)| < ε,则迭代停止。
4) 输出参数估值,根据σ02=VTQ-1V/(m-n)求得单位权中误差。
经过上述迭代方法即可得到方程
为了分析上述3种TLS算法和LS拟合线性回归方程的效果,利用文献[10](其自变量和因变量都含有随机误差,不含粗差)提供的观测数据,对选择不同的自变量和因变量的直线方程y=ax+b、x=ay+b求解拟合方程,计算结果如表 1所示。
| 表 1 几种TLS算法求解参数结果 Tab.1 Results of Several TLS Methods |
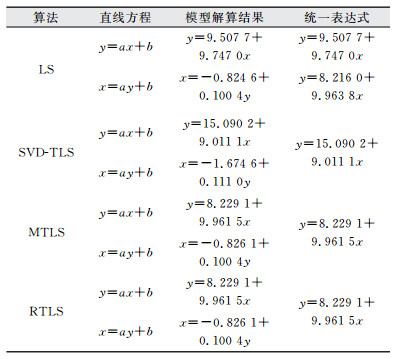 |
从表 1可看出,交换自变量和因变量使得利用LS拟合出的结果不一致,而对利用TLS算法拟合的结果无影响,其中,利用MTLS和RTLS拟合的表达式相同[14]。这是因为LS没有考虑自变量的误差,只能保证一个方向上的最佳估值。而TLS拟合直线的实质为采用测点到拟合直线的正交距离的平方和最小的准则,并把自变量视为含有误差的观测量,这使得拟合的结果整体效果最佳,因此交换自变量对利用TLS拟合的直线无影响。利用SVD-TLS与利用MTLS或RTLS拟合的直线方程不一致,这是因为SVD-TLS虽然考虑了线性回归模型中系数矩阵B的误差,但是它们默认系数矩阵中不含误差的常数列也含有误差;而MTLS和RTLS在考虑自变量误差的同时又只顾及了平差模型中系数矩阵含误差的部分。综合分析来看,在利用TLS拟合直线时,应选择拟合效果较好的MTLS或RTLS。
2.2 GPS水准拟合为了分析TLS在GPS水准拟合中的效果,使用某市城区80组GPS联测水准的高程数据,将其中的65组数据作为拟合数据,剩下的15组数据作为检验数据,如图 1所示。将利用抗差LS拟合的结果作为参考,分别采用LS、SVD-TLS、MTLS和RTLS拟合一次曲面ζ=a0+a1x+a2y和二次曲面ζ=a0+a1x+a2y+a3xy+a4x2+a5y2,表 2和表 3分别列出了利用4种方法拟合一次曲面和二次曲面的系数及对应单位权中误差。
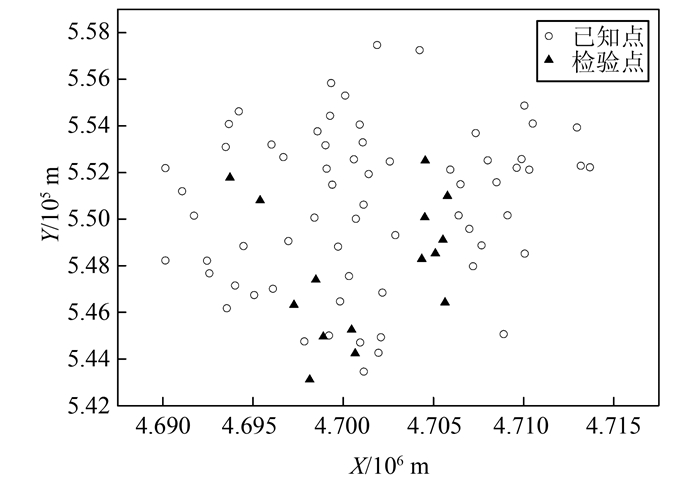 |
| 图 1 GPS水准点 Fig.1 Benchmark of GPS |
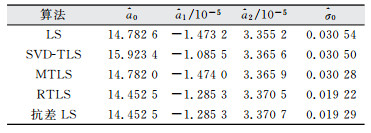
| 表 2 一次曲面拟合结果及精度/m Tab.2 Coefficients and Precision of the Equation/m |
 |
| 表 3 二次曲面拟合结果及精度/m Tab.3 Coefficients and Precision of the Equation/m |
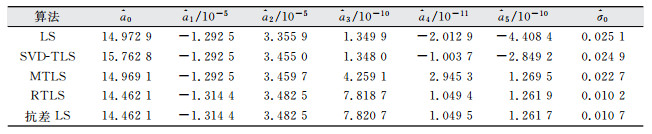 |
从表 2和表 3列出的拟合系数都可以看出,利用SVD-LS拟合曲面的系数与利用LS和MTLS拟合曲面的系数相差较大,这是因为在利用SVD-LS拟合过程中对系数矩阵中不含误差的列向量也进行了改正。利用RTLS拟合曲面的系数与利用LS、SVD-LS和MTLS拟合曲面的系数均不一致,这是因为在利用RTLS拟合过程中利用选权迭代法去除了粗差。从表 2和表 3列出的单位权中误差可以看出,利用TLS拟合曲面的单位权中误差优于LS,这是因为LS在曲面拟合中只考虑了观测向量ζ的误差,未顾及系数矩阵存在的误差;利用MTLS拟合曲面的单位权中误优于LS和SVD-TLS,这是因为在利用MTLS拟合过程中合理的考虑了系数矩阵中含有误差的列向量;利用RTLS拟合曲面的单位权中误差明显优于LS、SVD-TLS和MTLS,这是因为拟合数据存在粗差,RTLS能较好剔除粗差,并且合理的估计了系数矩阵中含有误差的部分。另外,与利用抗差LS拟合曲面的系数和单位权中误差相比,利用MTLS拟合的结果与抗差LS拟合的结果近乎一致[14]。
分别利用MTLS和抗差LS拟合的一次曲面和二次曲面进行外部检核,结果如图 2所示。
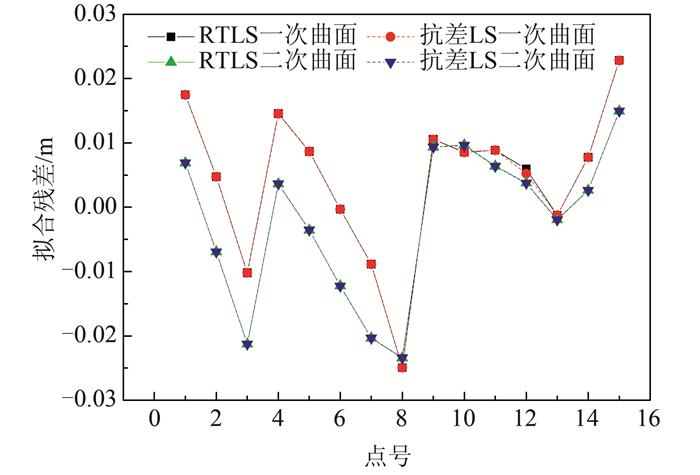 |
| 图 2 高程异常的外部检验 Fig.2 External Inspection of Height Anomaly |
从图 2可看出,利用抗差LS与RTLS拟合的曲面估计高程异常结果几乎一致,并且利用两种方法得到的二次曲面的拟合效果优于利用一次曲面拟合的结果。值得注意的是,与抗差LS相比,虽然利用RTLS通过拟合二次曲面方程得到的高程异常的单位权中误差精度没有明显提高,但RTLS对观测向量和系数矩阵中含有误差都进行了最小化约束,因此RTLS更适用于GPS水准拟合。
3 结束语为评价RTLS在GPS水准拟合中的应用效果,重点讨论了SVD-TLS、MTLS和RTLS的平差准则以及测量处理模型,将一种加权稳健总体最小二乘(RTLS)迭代算法应用于水准拟合。采用实验数据分析了LS与TLS的差异性,以利用抗差TLS拟合的高程异常值为参考,分析了RTLS在高程异常拟合中效果,得出以下结论:
1) 与LS相比,TLS同时顾及系数矩阵和观测向量中存在的误差,因此选择不同的自变量仍能得到一致的结果;而LS只有在系数矩阵没有误差时,所求结果才是无偏的。值得注意的是,SVD-TLS默认系数矩阵中所有元素都含有误差,而MTLS和RTLS仅考虑了系数矩阵存在误差的部分。
2) 在利用TLS进行GPS水准拟合时,利用RTLS拟合的结果优于利用SVD-TLS和MTLS拟合的结果。另外,利用RTLS拟合的高程异常的精度与利用抗差LS拟合的精度近乎一致,并且RTLS合理的估计了系数矩阵中含有误差的部分,因此,更适用于GPS水准拟合。
| [1] |
范东明. 任意平面网坐标自动解算的非线性最小二乘平差算法[J]. 铁道学报, 2002, 24(4): 78-82. DOI:10.3321/j.issn:1001-8360.2002.04.017 |
| [2] |
刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报·信息科学版, 2013, 38(5): 505-512. |
| [3] |
孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报·信息科学版, 2010, 35(6): 711-714. |
| [4] |
Schaffrin B, Wieser A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. DOI:10.1007/s00190-007-0190-9 |
| [5] |
丁克良, 沈云中, 欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(1): 44-47. DOI:10.3969/j.issn.1008-0562.2010.01.012 |
| [6] |
鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报·信息科学版, 2008, 33(5): 504-507. |
| [7] |
杨仕平, 范东明, 龙玉春. 整体最小二乘法平面坐标转换在基坑水平位移监测中的应用[J]. 测绘与空间地理信息, 2012, 35(9): 221-223. DOI:10.3969/j.issn.1672-5867.2012.09.074 |
| [8] |
邓罡. GPS高程拟合代替水准测量研究[D].长沙:中南大学,2012
|
| [9] |
黄令勇, 吕志平, 任雅奇, 等. 多元总体最小二乘在三维坐标转换中的应用[J]. 武汉大学学报·信息科学版, 2014, 39(7): 793-798. |
| [10] |
王乐洋, 许才军. 总体最小二乘研究进展[J]. 武汉大学学报·信息科学版, 2013, 38(7): 850-856. |
| [11] |
鲁铁定, 周世健, 王乐洋. 混合总体最小二乘的迭代解算算法[J]. 数据采集与处理, 2015(4): 802-809. |
| [12] |
汪奇生, 杨德宏, 杨腾飞. 线性回归模型的稳健总体最小二乘解算[J]. 大地测量与地球动力学, 2015, 35(2): 239-242. |
| [13] |
鲁铁定, 宁津生, 周世健, 等. 最小二乘配置的QR分解解法[J]. 辽宁工程技术大学学报(自然科学版), 2009, 28(4): 550-553. DOI:10.3969/j.issn.1008-0562.2009.04.010 |
| [14] |
刘小龙, 邱卫宁, 杨克明, 等. 混合LS-TLS的GM(1, 1)模型在基坑水平位移监测中的应用[J]. 测绘地理信息, 2014, 39(6): 36-38. |
 2018, Vol. 43
2018, Vol. 43


