| 一种无需水平信息的测月天文定向方法 |
2. 信息工程大学地理空间信息学院,河南 郑州,450001;
3. 61081部队,北京,100094
2. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450001, China;
3. 61081 Troops, Beijing 100094, China
通过观测自然天体实现天文定位定向具有隐蔽、无源、无误差累积等优点[1-4]。随着光学敏感元件和数字图像处理技术的发展,利用高性能相机代替人眼观测天体,实现天文定位定向成为一种趋势[5-9]。在夜晚的天球上,月球的视半径和星等远大于恒星和其他行星,可作为理想的天文观测目标[10]。文献[11]基于鱼眼相机敏感月球成像,利用倾角传感器作为媒介标定相机姿态,利用天文计时器记录相机曝光瞬间的精确时刻,解算得到相机坐标系x轴在地平坐标系下的指向,即实现了测月天文定向。文献[12]在海上基于鱼眼相机对月球和水天线同时成像,利用水天线作为水平基准标定相机姿态,进而实现海上测月天文定向。这两种方法均需要依赖外部手段敏感水平信息解算相机姿态。
本文提出一种无需水平信息的测月天文定向方法,即仅用鱼眼相机和天文计时器实现航向角确定。
1 月心位置序列为实现测月定向,需要标定相机坐标系和地平坐标系之间的旋转关系,本文通过分别计算月心在相机坐标系和地平坐标系下的位置序列进而达到这一目的,本节将详细介绍这两种月心位置序列的计算方法。
1.1 相机坐标系如图 1所示,定义O -XcYcZc为相机坐标系,原点O位于相机的光学中心,Zc轴指向主光轴方向,Xc轴与电荷耦合器件(charge-coupled device, CCD)平面坐标系的x轴平行,Yc轴按右手定则确定。主光轴与CCD平面的交点O′为像主点,M′为像点,M为物方点。M在相机坐标系下的坐标可采用方位角Ac和半视场角θc表示。
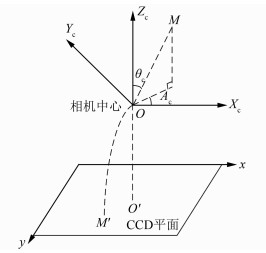 |
| 图 1 相机坐标系 Fig.1 Camera Coordinate System |
已知月心像点M′坐标(x, y),根据所选鱼眼镜头的投影模型和畸变模型,利用像主点O′坐标(x0, y0)、焦距f和径向畸变参数(k1, k2, k3),可计算出月心物方点M在相机坐标系下的半视场角[13, 14]:
| $ \begin{align} & {{\theta }_{c}}=2\arcsin \frac{r}{2f}+{{k}_{1}}{{(\arcsin \frac{r}{2f})}^{2}}+ \\ & {{k}_{2}}{{(\arcsin \frac{r}{2f})}^{3}}+{{k}_{3}}{{(\arcsin \frac{r}{2f})}^{4}} \\ \end{align} $ | (1) |
其中r为像点至像主点的距离,即
| $ r=\sqrt{{{(x-{{x}_{0}})}^{2}}+{{(y-{{y}_{0}})}^{2}}} $ | (2) |
根据像点M′与像主点O′的坐标关系,计算出月心物方点M在相机坐标系下的方位角:
| $ {{A}_{c}}\mathrm{=}\left\{ \begin{align} & \text{arctan}\frac{y-{{y}_{0}}}{{{x}_{0}}-x}, {{x}_{0}}-x>0, y-{{y}_{0}}>0 \\ & \arctan \frac{y-{{y}_{0}}}{{{x}_{0}}-x}+\text{ }\!\!\pi\!\!\text{ , }{{x}_{0}}-x<0 \\ & \text{arctan}\frac{y-{{y}_{0}}}{{{x}_{0}}-x}+2\text{ }\!\!\pi\!\!\text{ }, {{x}_{0}}-x>0, y-{{y}_{0}}<0 \\ \end{align} \right. $ | (3) |
可将(Ac, θc)化为三维直角坐标
| $ {\boldsymbol{S}} _ { c } = \left[ \begin{array} { l } { X _ { c } } \\ { Y _ { c } } \\ { Z _ { c } } \end{array} \right] = \left[ \begin{array} { l } { \operatorname { sin } \theta _ { c } \operatorname { cos } A _ { c } } \\ { \operatorname { sin } \theta _ { c } \operatorname { sin } A _ { c } } \\ { \operatorname { cos } \theta _ { c } } \end{array} \right] $ | (4) |
利用鱼眼相机对月球连续敏感成像n次,即可得到一组月心在相机坐标系下的位置序列{ Sc1, Sc2, Sc3, …, Scn}。
1.2 地平坐标系如图 2所示,定义O -XhYhZh为地平坐标系,O为测站中心,Xh轴指向正南方向,Zh轴指向天顶方向,Yh轴按左手定则确定。M为月心位置,则M在地平坐标系下的坐标可用方位角A和高度角h表示。P为北天极,则PMZh构成球面三角形,其中,
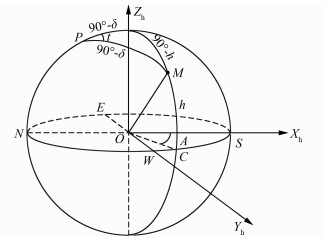 |
| 图 2 地平坐标系 Fig.2 Horizon Coordinate System |
根据球面三角形边的余弦公式可得:
| $ \begin{align} & \cos ({{90}^{\circ }}-h)=\cos ({{90}^{\circ }}-\varphi )\cos ({{90}^{\circ }}-\delta )+ \\ & \ \ \ \ \ \ \ \sin ({{90}^{\circ }}-\varphi )\sin ({{90}^{\circ }}-\delta )\cos t \\ \end{align} $ | (5) |
化简得:
| $ \sin h=\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos t $ | (6) |
方位角A一般可根据时角法计算得到:
| $ \tan A=\frac{\cos \delta \sin t}{\sin \varphi \cos \delta \cos t-\sin \delta \cos \varphi } $ | (7) |
式(6)、式(7)中,月心时角t的计算公式为:
| $ t={{S}_{0}}+{{T}_{\text{ut1}}}+\lambda -\alpha $ | (8) |
式中,α为月心观测赤经。λ为测站天文经度,Tut1为相机曝光瞬间对应的格林尼治一类世界时(universal time, UT1)时刻,需要通过对应的协调世界时(universal time coordinated, UTC)时刻Tutc进行化算,进而需要查阅国际地球自转服务(international earth rotation service, IERS)定期发布的bulletina公报。S0为世界时0时对应的格林尼治恒星时,计算公式为:
| $ \begin{array}{l} {S_0} = 6\;{\rm{h41}}\;{\rm{min50}}{\rm{.548}}\;{\rm{41}}\;{\rm{s + 8}}\;{\rm{640}}\;{\rm{184}}{\rm{.812}}\;{\rm{866s}} \cdot \\ \;\;\;\;\;\;\;{T_G} + 0.{\rm{093}}\;{\rm{104}}\;{\rm{s}} \cdot T_G^2 + \Delta \psi \cdot {\rm{cos\varepsilon }}/15 \end{array} $ | (9) |
式中,Δψ为黄经章动; ε为黄赤交角; TG为格林尼治日期对应的儒略世纪数。
需要注意的是,由于相机坐标系是右手系,为了与其建立联系,这里将地平坐标系Yh轴反向变为右手系O -Xh′Yh′Zh′,于是将(A, h)化为三维直角坐标为
| $ {\boldsymbol{S}_{h'}} = \left[ \begin{array}{l} {X_{h'}}\\ {Y_{h'}}\\ {Z_{{s_{h'}}}} \end{array} \right] = \left[ \begin{array}{l} \cos h\cos A\\ - \cos h\cos A\\ \sin h \end{array} \right] $ | (10) |
利用鱼眼相机对月球连续敏感成像n次,即可得到一组月心在地平坐标系(右手系)下的位置序列{ Sh′1, Sh′2, Sh′3, …, Sh′n}。
2 测月定向原理定义Rch′为坐标系O -XcYcZc转换到坐标系O -Xh′Yh′Zh′的旋转矩阵,则
| $ {{\boldsymbol{S}}_{{{h}'}}}=\boldsymbol{R}_{c}^{{{h}'}}\cdot {{\boldsymbol{S}}_{c}} $ | (11) |
一般地,定义将O -XcYcZc转换到O -Xh′Yh′Zh′需要经过以下3次旋转:
1) 绕Xc轴旋转γ角,旋转矩阵记作RX(γ);
2)绕Yc轴旋转ψ角,旋转矩阵记作RY(ψ);
3) 绕Zc轴旋转ξ角,旋转矩阵记作RZ(ξ)。
即
| $ \boldsymbol{R}_{c}^{{{h}'}}={{\boldsymbol{R}}_{Z}}(\xi ){{\boldsymbol{R}}_{Y}}(\psi ){{\boldsymbol{R}}_{X}}(\gamma ) $ | (12) |
展开后得:
| $ {{\boldsymbol{R}}^{{{h}'}}}_{c}=\left[ \begin{matrix} \cos \psi \cos \xi & \sin \gamma \sin \psi \cos \xi +\cos \gamma \sin \xi & -\cos \gamma \sin \psi \cos \xi +\sin \gamma \sin \xi \\ -\cos \psi \sin \xi & -\sin \gamma \sin \psi \sin \xi +\cos \gamma \cos \xi & \cos \gamma \sin \psi \sin \xi +\sin \gamma \cos \xi \\ \sin \psi & -\sin \gamma \cos \psi & \cos \gamma \cos \psi \\ \end{matrix} \right] $ | (13) |
所求航向角为:
| $ \xi =-\text{arctan}\frac{\boldsymbol{R}_{c}^{{{h}'}}(2, 1)}{\boldsymbol{R}_{c}^{{{h}'}}(1, 1)} $ | (14) |
因此,要实现测月定向,需要求得旋转矩阵R ch′。若利用式(13)求解旋转矩阵会引入大量繁琐的三角函数计算,为解决该问题,这里引入罗德里格参数(a, b, c)表示旋转矩阵。根据罗德里格矩阵的定义,旋转矩阵均可由反对称矩阵Q和单位阵I表示[15],故
| $ \boldsymbol{R}_{c}^{{{h}'}}=(\boldsymbol{I}+\boldsymbol{Q}){{(\boldsymbol{I}-\boldsymbol{Q})}^{-1}} $ | (15) |
其中,
| $ \begin{matrix} \boldsymbol{Q}=\left[ \begin{matrix} 0 & -c & -b \\ c & 0 & -a \\ b & a & 0 \\ \end{matrix} \right] & ;\boldsymbol{I}\mathit{=}\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \\ \end{matrix} $ | (16) |
则式(11)变为:
| $ \left[ \begin{array}{l} {X_{h'}}\\ {Y_{h'}}\\ {Z_{h'}} \end{array} \right] = ({\boldsymbol{I}} + {\boldsymbol{Q}}){({\boldsymbol{I}} - {\boldsymbol{Q}})^{ - 1}}\left[ \begin{array}{l} {X_c}\\ {Y_c}\\ {Z_c} \end{array} \right] $ | (17) |
罗德里格旋转矩阵R ch′具有如下性质[16]:
| $ (\boldsymbol{I}+\boldsymbol{Q}){{(\boldsymbol{I}-\boldsymbol{Q})}^{-1}}={{(\boldsymbol{I}-\boldsymbol{Q})}^{-1}}(\boldsymbol{I}+\boldsymbol{Q}) $ | (18) |
将式(18)代入式(17)并整理得:
| $ ({\boldsymbol{I}} - {\boldsymbol{Q}})\left[ \begin{array}{l} {X_{h'}}\\ {Y_{h'}}\\ {Z_{h'}} \end{array} \right] = ({\boldsymbol{I}} + {\boldsymbol{Q}})\left[ \begin{array}{l} {X_c}\\ {Y_c}\\ {Z_c} \end{array} \right] $ | (19) |
由此可列误差方程:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}}\\ {{v_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{ - {Z_{h'}} - {Z_c}}&{ - {Y_{h'}} - {Y_c}}\\ { - {Z_{h'}} - {Z_c}}&0&{{X_{h'}} + {X_c}}\\ {{Y_{h'}} + {Y_c}}&{{X_{h'}} + {X_c}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} a\\ b\\ c \end{array}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ \begin{array}{l} {X_{h'}} - {X_c}\\ {Y_{h'}} - {Y_c}\\ {Z_{h'}} - {Z_c} \end{array} \right] \end{array} $ | (20) |
式(20)中只有两个独立方程,因此在实测中至少需要对月球观测两次才能解算出a、b、c 3个罗德里格参数并确定旋转矩阵R ch′,进而根据式(14)实现航向角解算。
3 试验2017年5月12日夜晚,天气状况良好,在中国华北地区某测站基于本方法进行了测月定向试验,对月球进行了两个时段的拍摄,每个时段约15 min,采集72幅月球图像。由于难以将相机中心与测站标志中心完全重合,故无法获取航向角真值,这里只能将各时段使用最大图像数量(即72幅图像)的定向结果作为基准衡量该方法的内符合定向精度。如图 3所示,蓝色散点代表时段1的内符合定向误差,红色散点代表时段2的内符合定向误差。
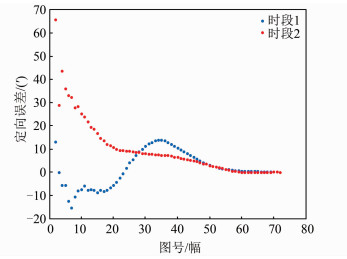 |
| 图 3 测月定向误差 Fig.3 Orientation Error Based on Lunar Observation |
由图 3可知,随着月球图像数量的增加,定向结果逐步趋于稳定,内符合定向精度逐渐提高,当采用40幅图像定向解算时,内符合定向误差优于10.3′; 当采用50幅图像定向解算时,内符合定向误差优于3.1′; 当采用60幅图像定向解算时,内符合定向误差优于27.1″; 当采用70幅图像定向解算时,内符合定向误差优于7.7″。需要说明的是,本文测月天文定向方法需要于月球在夜空下完全可视、不被遮挡的条件下进行,这样可保证在相机拍摄的月球图像中能有效提取到月球中心位置,进而用于定向解算。
4 结束语本文通过计算月球中心在相机坐标系和地平坐标系下的位置序列求解得到两个坐标系的旋转关系,进而实现了测月天文定向。这种方法摆脱了对水平信息的依赖,理论上可规避因倾角传感器、水天线等水平敏感源引入的附加误差,同时也能降低设备复杂度。经实测试验表明,当观测次数足够多时,定向结果逐渐收敛,内符合定向精度随观测次数的增加而上升。事实上,本文方法同样可扩展到拍摄恒星、太阳等天体实现天文定向,也可研究月球被云雾遮挡条件下的月球中心提取方法,进而实现适应性更强的测月天文定向方法,未来可进行相关的研究与试验继续探索。
| [1] |
张超, 郑勇, 孟凡玉. 利用测日实现快速天文定向[J]. 测绘科学技术学报, 2007, 24(5): 343-345. DOI:10.3969/j.issn.1673-6338.2007.05.009 |
| [2] |
李小军, 殷志祥, 蔡顺中. 月面探测器天文导航研究[J]. 测绘地理信息, 2015, 40(4): 26-28. |
| [3] |
李夫鹏, 张超, 王正涛, 等. 天文/GNSS组合定向系统研究[J]. 测绘地理信息, 2017, 42(5): 25-28. |
| [4] |
郁丰, 熊智, 屈蔷. 基于多圆交汇的天文定位与组合导航方法[J]. 宇航学报, 2011, 32(1): 88-92. DOI:10.3873/j.issn.1000-1328.2011.01.013 |
| [5] |
何炬. 国外天文导航技术发展综述[J]. 舰船科学技术, 2005, 27(5): 91-96. |
| [6] |
王安国. 现代天文导航及其关键技术[J]. 电子学报, 2007, 35(12): 2 347-2 353. |
| [7] |
Hirt C, Bürki B, Somieski A, et al. Modern Determination of Vertical Deflections Using Digital Zenith Cameras[J]. Journal of Surveying Engineering, 2010, 136(1): 1-12. DOI:10.1061/(ASCE)SU.1943-5428.0000009 |
| [8] |
李崇辉. 基于鱼眼相机的舰船天文导航技术研究[D]. 郑州: 信息工程大学, 2013
|
| [9] |
詹银虎. 测日天文导航理论及技术研究[D]. 郑州: 信息工程大学, 2015
|
| [10] |
蒲俊宇, 郑勇, 李崇辉, 等. 一种能适应月相变化的月球图像中心提取算法[J]. 测绘科学技术学报, 2017, 34(5): 461-465. |
| [11] |
蒲俊宇, 郑勇, 李崇辉, 等. 超大视场测月天文定向方法[J]. 测绘学报, 2018, 47(4): 435-445. |
| [12] |
Pu Junyu, Li Chonghui, Zheng Yong, et al. Astronomical Vessel Heading Determination based on Simultaneously Imaging the Moon and the Horizon[J]. Journal of Navigation, 2018, 71(5): 1 247-1 262. DOI:10.1017/S0373463318000073 |
| [13] |
胡学敏, 郑宏, 郭琳, 等. 利用鱼眼相机对人群进行运动估计[J]. 武汉大学学报·信息科学版, 2017, 42(4): 537-542. |
| [14] |
王永仲. 鱼眼镜头光学[M]. 北京: 科学出版社, 2006.
|
| [15] |
原玉磊, 蒋理兴, 刘灵杰. 罗德里格矩阵在坐标系转换中的应用[J]. 测绘科学, 2010, 35(2): 178-179. |
| [16] |
赵启龙. 罗德里格矩阵在三维坐标转换中的应用研究[J]. 北京测绘, 2014(5): 29-30. DOI:10.3969/j.issn.1007-3000.2014.05.008 |
 2021, Vol. 46
2021, Vol. 46

