| 中国区域CODE全球电离层地图精度分析 |
电离层延迟是GNSS定位的主要误差源之一。为了削弱电离层延迟对定位精度的影响,许多学者采用不同建模方法建立了不同的电离层改正模型[1-4],其中较为简单便捷的有Klobuchar、Nequick等经验模型,其使用的计算系数少,运算速率快,但改正精度有限[5]。为获取更高精度的电离层改正,用户可采用星基增强系统(satellite-based augmentation system, SBAS)提供的信息,但SBAS只能在北美、欧洲、日本等地区使用[6]。全球范围内可供使用的电离层产品有IGS(international GNSS service)电离层分析中心以电离层交换格式(ionosphere map exchange format,IONEX)提供的快速及最终全球电离层地图(global ionospheric map, GIM),其中欧洲轨道确定中心(Center Orbit Determination Europe, CODE)同时还提供1 d、2 d、5 d的电离层预报产品[7, 8]。此外,法国空间研究中心(Centrenational d’Etudes Spatiales, CNES)通过实时服务(real-time service,RTS)提供实时电离层产品。
许多学者对电离层特性及不同电离层产品进行了研究。韩吉德等[9]对GIM的时空特性进行了分析,发现电离层在赤道附近东经75°~120°处异常活跃。陈秀德等[10]对不同最终GIM产品进行了精度分析,发现在高纬度地区,美国喷气推进实验室的GIM精度较高,中低纬度地区CODE的GIM精度较高。Liu等[11]将中国科学院提供的电离层最终GIM进行了精度验证,发现其与CODE最终GIM的VTEC(vertical total electron content)精度都能达到1.0~2.5 TECU,喷气推进实验室的最终GIM普遍呈现正偏差,但其他IGS电离层分析中心的最终GIM普遍呈现负偏差。Nie等[12]将CNES提供的实时产品应用在实时单频精密单点定位中,发现其精度能在水平方向达到亚米级,在高程方向达到米级。
然而,以上对GIM产品的分析多集中在全球范围,对于中国区域而言,可用的IGS站非常少,因此GIM产品的精度较其他区域也会相对较低。CODE GIM在中国区域的精度研究较少,需要进一步探讨。本文对CODE最终GIM在中国区域的精度进行了分析,以2017年1月1日-7日的CODE GIM为例,在中国区域不同纬度范围内选取了25个均匀分布的陆态网基准站,首先分析了STEC(slant total electron content)精度,然后评估了应用CODE GIM的单频动态定位精度。
1 CODE GIM产品CODE采用15×15阶球谐函数模型表达电离层电子分布,假定电离层中所有电子集中在一个离地球表面450 km的薄层上[13-15],利用电离层穿刺点(ionospheric pierce point,IPP)处的电子含量反映通过该点天顶方向的总电子含量(vertical total electron content,VTEC)。
CODE使用经度分辨率为5°、纬度分辨率为2.5°、时间分辨率为1 h的格网提供VTEC产品,用户可以通过ftp网站(ftp.unibe.ch/aiub/CODE/)免费下载。CODE使用了来自全球约300个测站的原始观测值每日生成CODE GIM,其滞后时间约为11 d。
利用获取的电离层地图,任意时刻处的VTEC值可以通过该时刻前后提供的电离层地图Ei=E(Ti)和Ei+1=E(Ti+1)内插得到,内插的计算式为[8]:
| $ E\left( {\beta , \lambda , t} \right) = \frac{{{T_{i + 1}} - t}}{{{T_{i + 1}} - {T_i}}}{E_i}\left( {\beta , \lambda } \right) + \frac{{t - {T_i}}}{{{T_{i + 1}} - {T_i}}}{E_{i + 1}}\left( {\beta , \lambda } \right) $ | (1) |
式中, t为世界时,且Ti≤t≤Ti+1; β和λ分别表示该点的地心纬度和经度。
任意位置处的VTEC值可以通过该点附近4个最近的格网点数值内插得到,计算式为[8]:
| $ \begin{array}{l} \;\;\;\;\;E\left( {{\lambda _0} + p\Delta \lambda , {\beta _0} + q\Delta \beta } \right) = \\ \;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\left( {1 - q} \right){E_{00}} + \\ p\left( {1 - q} \right){E_{10}} + q\left( {1 - p} \right){E_{01}} + pq{E_{11}} \end{array} $ | (2) |
式中, 0≤p≤1,0≤q≤1; Δλ和Δβ分别为格网的经度和纬度间隔。
2 实验与分析选取2017年1月1日-7日的CODE GIM进行精度分析,在此期间电离层相对稳定。以25个均匀分布的陆态网基准站为研究对象,其中BJFS、LHAZ、SHAO、URUM、WUHN 5个测站为IGS测站。精度分析分为两部分,首先是STEC精度比较;其次是定位精度分析。考虑到地理因素,将中国区域按纬度划分为纬度值β < 30°、30°≤β < 40°、40°≤β < 50°、β≥50°的4个区域进行分析。
2.1 与双频观测值计算所得STEC比较CODE在发布GIM的同时,会发布卫星的DCB(differential code bias),然而,尚无产品发布陆态网站点接收机的DCB。以接收机双频观测值测定的STEC值为参考,其计算式为:
| $ {\rm{STEC}} = \frac{{{f_1}^2f_2^2}}{{40.3\left( {f_1^2 - f_1^2} \right)}}(\mathop {{P_4}}\limits^ \sim - {\rm{DC}}{{\rm{B}}_j} - {\rm{DC}}{{\rm{B}}^i}) $ | (3) |
式中,f1和f2为载波频率;
本文首先估计陆态网站点接收机的DCB。估计方法为固定卫星DCB,对中国区域电离层进行多项式建模,同时估计多项式模型系数和接收机DCB。为了验证接收机DCB估计的准确性,以CODE提供的IGS站DCB为参考,估值与参考值如图 1所示,估值与参考值的偏差如表 1所示。数据采集时期内WUHN站的DCB值未给出。
| 表 1 2017年1月1日-7日的4个IGS站接收机DCB估计值与参考值的偏差/ns Tab.1 Bias Between Estimated DCB of Receiver and Reference Value at 4 IGS Stations During January 1-7, 2017/ns |
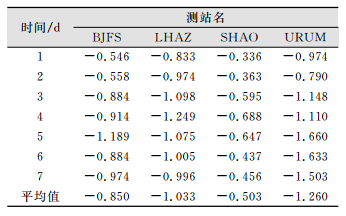 |
由表 1和图 1可知,DCB估值与参考值的偏差为-1.660~-0.336 ns,7d内BJFS、LHAZ、SHAO、URUM 4个IGS站的平均偏差分别为-0.850 ns、-1.033 ns、-0.503 ns、-1.260 ns,平均值为-0.912 ns,因此可认为接收机DCB估值与CODE的接收机DCB在同等精度水平。
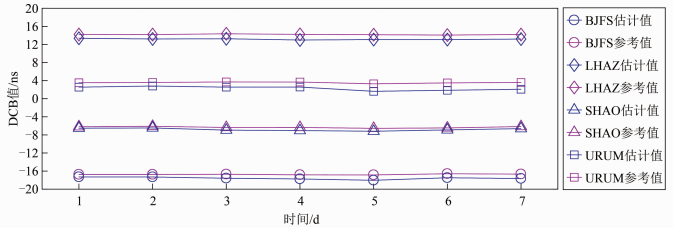 |
| 图 1 2017年1月1日-7日的4个IGS站接收机DCB估计值与参考值 Fig.1 The Estimated and Reference Values for DCB of Receivers at 4 IGS Stations During January 1-7, 2017 |
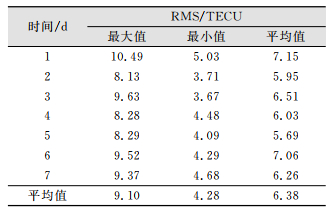
2017年1月1日-7日的25个测站的STEC精度如表 2所示,其均方根(root mean square, RMS)的平均值为6.38 TECU。7 d内的RMS的最大值、最小值、平均值在数值上都相近,三者的分布区间分别为8.28~10.49 TECU、3.67~5.03 TECU、6.03~7.15 TECU,间接表明7 d内电离层活跃程度相近。考虑到电离层活跃程度与纬度有强相关性,为了进一步分析CODE GIM在中国区域的精度,如图 2所示,对STEC精度进行了分纬度统计。2017年1月1日-7日中国区域内4个站纬度范围的RMS平均值分别为8.23 TECU、6.59 TECU、5.25 TECU、4.52 TECU。随着纬度增大,利用CODE GIM所得的STEC值与参考值的偏差(BIAS)明显减小,且在高纬度地区,数据离散程度更小。这是由于电离层在高纬度地区活跃强度较小,VTEC数值较小。
| 表 2 2017年1月1日-7日25个测站应用CODE GIM的STEC精度统计 Tab.2 STEC Accuracy of 25 Stations with CODE GIM During January 1-7, 2017 |
 |
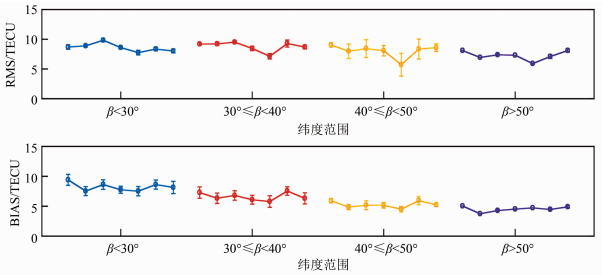 |
| 图 2 2017年1月1日-7日的25个测站STEC精度分纬度统计图 Fig.2 Accuracy of STEC for 25 Stations in Terms of Latitude During January 1-7, 2017 |
2.2 单频动态定位实验
为了分析CODE GIM对单频动态定位精度的影响,应用CODE GIM进行单频动态精密单点定位,截止高度角设置为15°,卫星星座为单GPS系统,参考坐标采用双频静态PPP进行解算。25个测站单频动态定位精度如图 3所示,统计表如表 3所示。定位精度明显与测站相关,表现最差的是测站GSTS,其N、E、U方向定位精度显著低于其他测站。7d内25个测站的N、E、U方向定位的平均RMS分别为0.570 m、0.594 m、1.178m。一天内测站N、E、U方向的RMS值区间分别为0.364~0.943 m,0.355~0.926 m,0.721~2.386m。U方向的定位精度明显比N、E方向差,N、E方向定位精度相当。说明应用CODE GIM进行单频动态定位精度在中国区域内高程方向达到米级,水平方向达到亚米级。
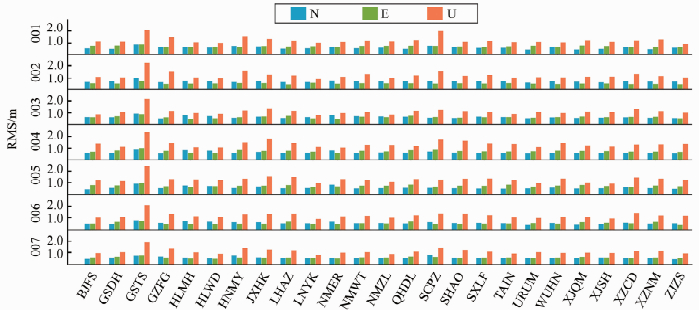 |
| 图 3 2017年1月1日-7日应用CODE GIM的单频动态定位RMS Fig.3 Single-Frequency Kinematic Positioning RMS with CODE GIM During January 1-7, 2017 |
| 表 3 2017年1月1日-7日应用CODE GIM的单频动态定位精度统计 Tab.3 Single-frequency Kinematic Positioning Accuracy with CODE GIM During January 1-7, 2017 |
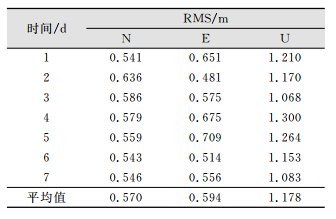 |
图 4显示了应用CODE GIM的单频动态定位1h间隔RMS的时间序列,N、E、U各方向的RMS值分别分布在0.190~1.164 m、0.177~1.198 m、0.449~2.879 m区间内,其RMS平均值分别为0.501 m、0.528 m、1.037 m,标准差分别为0.194 m、0.214 m、0.348 m。水平方向的RMS值分布较为集中,U方向的RMS值明显比水平方向大,且分布较为离散。同样说明水平定位精度能达到亚米级,优于米级高程精度。
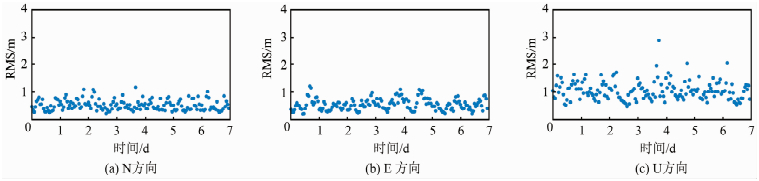 |
| 图 4 2017年1月1日-7日应用CODE GIM的单频动态定位1h间隔RMS时间序列 Fig.4 Time Series of RMS Distribution for Single-Frequency Kinematic Positioning with CODE GIM in 1h Interval During January 1-7, 2017 |
图 5显示了应用CODE GIM的单频动态定位分纬度精度,无论在哪个纬度范围,水平方向RMS值明显比高方向小,且分布更集中。随着纬度升高,定位精度略有提升,但纬度β≥50°范围内水平方向定位精度明显比40°≤β < 50°范围内差,可能与纬度β≥50°范围内所选测站数目过少有关。
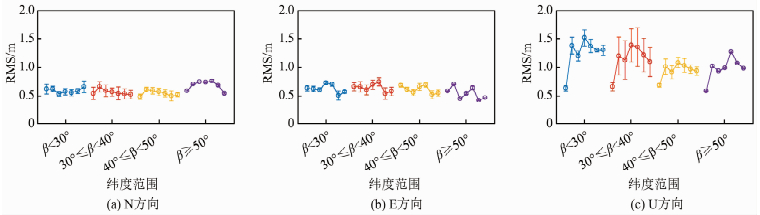 |
| 图 5 2017年1月1日-7日应用CODE GIM的单频动态定位分纬度RMS Fig.5 RMS Distribution of Single-Frequency Kinematic Positioning with CODE GIM in Terms of Latitude During January 1-7, 2017 |
3 结束语
本文在中国区域不同纬度范围内选取了25个均匀分布的陆态网基准站,从STEC精度及单频精密单点定位精度两个方面对CODE电离层地图在中国区域内的精度进行了评估。尽管CODE GIM在全球的精度为2~8 TECU,但是本文研究结果显示,中国区域CODE GIM的精度较差。结果表明STECRMS 7 d内的平均值为6.38 TECU,各测站一天内STECRMS分布区间为3.67~10.49 TECU。7 d内25个测站的N、E、U方向定位的RMS平均值分别为0.570 m、0.594 m、1.178 m。1 h内测站N、E、U方向的RMS平均值分别为0.501 m、0.528 m和1.037 m,标准差分别为0.194 m、0.214 m和0.348 m。应用CODE GIM进行单频动态精密单点定位精度在平面达到亚米级,高程方向达到米级。
| [1] |
曹文涛, 郭际明, 谢翔, 等. 基于CORS的电离层延迟建模方法[J]. 测绘地理信息, 2013, 38(3): 12-16. |
| [2] |
刘磊, 姚宜斌, 孔建, 等. 附加GIM约束的全球电离层建模[J]. 大地测量与地球动力学, 2017(1): 67-71. |
| [3] |
吴寒, 吴燕苹, 吴亚君, 等. 一种基于卫星轨迹的电离层区域建模方法[J]. 测绘通报, 2017(10): 130-133. |
| [4] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报·信息科学版, 2011, 36(3): 267-270. |
| [5] |
Klobuchar J A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325-331. DOI:10.1109/TAES.1987.310829 |
| [6] |
Zhang L, Yao Y, Peng W, et al. Real-Time Global Ionospheric Map and Its Application in Single-Frequency Positioning[J]. Sensors, 2019, 19: 1138. DOI:10.3390/s19051138 |
| [7] |
Feltens J, Schaer S. IGS Products for the Ionosphere[C]. Proceedings of the 1998 IGS Analysis Center Workshop, Darmstadt, Germany, 1998
|
| [8] |
Schaer S, Gurtner W, Feltens J. IONEX: The IONosphere Map EXchange Format Version 1[S]. Berne, Swiss: University of Berne, 1998
|
| [9] |
韩吉德, 王祖顺, 王春青. 全球电离层时空变化特性分析[J]. 测绘地理信息, 2012, 37(6): 26-29. |
| [10] |
陈秀德, 贾小林, 朱永兴, 等. 不同电离层格网产品的精度分析[J]. 大地测量与地球动力学, 2017(8): 849-855. |
| [11] |
Liu A, Wang N, Li Z, et al. Validation of CAS's Final Global Ionospheric Maps During Different Geomagnetic Activities From 2015 to 2017[J]. Results in Physics, 2018, 10: 481-486. DOI:10.1016/j.rinp.2018.06.057 |
| [12] |
Nie Z, Yang H, Zhou P, et al. Quality Assessment of CNES Real-time Ionospheric Products[J]. GPS Solutions, 2019, 23: 11. DOI:10.1007/s10291-018-0802-2 |
| [13] |
Schaer S. Mapping and Predicting the Earth's Ionosphere Using the Global Positioning System[D]. Eidg: Technische Hochschule Zürich, 1999
|
| [14] |
姚宜斌, 陈鹏, 吴寒, 等. 2011年3月11日日本地震震前电离层异常变化分析[J]. 科学通报, 2012, 57(5): 355-365. |
| [15] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227. |
 2021, Vol. 46
2021, Vol. 46

