| WiFi室内定位测站布设优化的DOP数值分析 |
2. 深圳市地籍测绘大队,广东 深圳,518034;
3. 武汉益士天慧科技有限公司,湖北 武汉,430200
2. Shenzhen Cadastral Surveying and Mapping Brigade, Shenzhen 518034, China;
3. Wuhan Yishi Tianhui Technology Co., Ltd., Wuhan 430200, China
随着市场对基于位置服务(location based service,LBS)需求的增加,室内定位已经逐渐成为研究的热门课题,智能终端和WiFi网络等技术的普及,极大地拓展了室内定位技术的发展方向。WiFi信号广泛存在于室内空间,包括家庭、商场、办公室和教室等各种场景,是一种较为理想的定位源[1, 2]。
目前,常见的WiFi定位算法包括接受信号强度(received signal strength index,RSSI)指纹匹配[3-5]和三角测量定位[6-9],很多研究者将定位精度改善的重点放在了具体的定位技术的研究与改进[3-9],但是对于测站节点的布设优化研究并不是很多。彭逸凡等[10]将空间位置精度因子用于UWB室内定位测站布设指导;侯全武等[11]研究了传感器位置对狭长空间定位精度的影响,但是没有考虑传感器布局的几何精度衰减因子;高虎等[12]研究了基于四站时差定位的星型布站,提出结合实际情况合理的布设测站可提高定位精度。对于室内测站节点的优化布设,类似于GNSS领域寻找最优的卫星星座空间几何布局,定位精度的卫星空间布局影响的评价指标通常是精度衰减因子(dilution of precision,DOP),较小的DOP值能获得较高的定位精度[13]。本文假设在5个WiFi接入点(access point,AP)(本文统称为测站节点)存在的前提下,共设计了5种测站布设方案,分别分析了4种形式DOP指标[14]:空间位置精度因子(position dilution of precision,PDOP)、几何精度衰减因子(geometric dilution of precision,GDOP)、平面位置精度因子(horizontal dilution of precision,HDOP)和垂直精度因子(vertical dilution of precision,VDOP)。在测距精度一定的前提下,对比分析了各种方案DOP值的结果,通过分析DOP值来优化测站节点布设,达到改善室内定位系统的定位精度。
1 DOP数值分析模型室内定位中,基于TOA(top of atmosphere)等需要精密测时的定位技术,在已知测站节点位置和钟参数的前提下,需要计算三维空间3个位置参数和1个接收机钟参数,为了能解算出上述4个参数,必须的测站节点数至少4个。对应的线性化伪距观测方程为式(1),其最小二乘解为式(2)[15]。
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{V}} $ | (1) |
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $ | (2) |
式中,L为测量伪距与在线性化点预测伪距间的差值;V为测量噪声;
| $ \mathit{\boldsymbol{A}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}_{x1}}}&{{\mathit{\boldsymbol{a}}_{y1}}}&{{\mathit{\boldsymbol{a}}_{z1}}}&1\\ {{\mathit{\boldsymbol{a}}_{x2}}}&{{\mathit{\boldsymbol{a}}_{y2}}}&{{\mathit{\boldsymbol{a}}_{z2}}}&1\\ \vdots & \vdots & \vdots & \vdots \\ {{\mathit{\boldsymbol{a}}_{xn}}}&{{\mathit{\boldsymbol{a}}_{yn}}}&{{\mathit{\boldsymbol{a}}_{xn}}}&1 \end{array}} \right]_{n \times 4}} $ | (3) |
式中,axi、ayi、azi (i = 1,2,…,n) 表示测站节点与待测节点位置之间的方向矢量余弦。
| $ {\mathit{\boldsymbol{a}}_{xi}} = \frac{{{\mathit{\boldsymbol{x}}^i} - {\mathit{\boldsymbol{x}}_\mu }}}{{{\mathit{\boldsymbol{R}}_i}}}\;\;\;\;\; , $ | (4) |
式中,xi为测站节点在X方向的分量;xμ表示待测节点位置在X方向上的分量;Ri为待测节点和测站节点位置的方向矢量。假定式(2)中L的误差协方差阵为σ2,按照误差传播定律,
| $ ∑ \hat{\mathit{\boldsymbol{{ X}}}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\sigma }}^2}\mathit{\boldsymbol{PA}}{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}} $ | (5) |
假设P为单位矩阵,则式(5)为:
| $ \sum {\hat{\mathit{\boldsymbol{ X}}} } = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{\sigma }}^2} $ | (6) |
则有
| $ \begin{array}{*{20}{l}} {{\rm{Diag}}} \end{array}{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}} = {\mathop{\rm Diag}\nolimits} \left( {{a_{11}}, {a_{22}}, {a_{33}}, {a_{44}}} \right) $ | (7) |
式中,a11、a22、a33、a44表示矩阵(ATA)-1对角线元素。则GDOP、PDOP、HDOP、VDOP可分别表示为:
| $ {\rm{GDOP}} = \sqrt {{a_{11}} + {a_{22}} + {a_{33}} + {a_{44}}} = \sqrt {{\mathop{\rm tr}\nolimits} \left( {{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)}^{ - 1}}} \right)} $ | (8) |
| $ {\rm{PDOP}} = \sqrt {{a_{11}} + {a_{22}} + {a_{33}}} $ | (9) |
| $ {\rm{HDOP}} = \sqrt {{a_{11}} + {a_{22}}} $ | (10) |
| $ {\rm{VDOP}} = \sqrt {{a_{33}}} $ | (11) |
GDOP的值取决于待测节点和测站节点之间的几何构型和设备之间钟差,当GDOP值越大时,待测节点和测站节点之间的几何布局对测距误差的放大程度越高,对定位精度的影响越大,在涉及需要考虑钟差因素的情况下,计算空间三维位置,应该考虑GDOP,以优化测站布局,提高定位精度[16]。根据卫星定位理论,各个卫星之间连线后构成的几何体的体积V与GDOP成反比[17],在体积V越大时GDOP最小,反之越大。GDOP值取得最小值时,卫星星座分布为最佳几何布局[18]。戴超[19]指出,GDOP最小值与可观测的卫星个数有关,并且随着卫星数目n的增多,GDOP的最小值也越来越小,定位精度也会相应的提高。同样,在室内为了取得最优的几何布局,测站布设也符合上述规律。在排除设备钟差因素的情况下,由式(9)可以得到三维的PDOP;由式(10)可得到二维的HDOP;由式(11)可得到高程方向的VDOP。
2 实验及分析 2.1 实验方案设计本文实验模拟环境为20 m×20 m×3 m大小室内空间,为了更加直观地说明测站节点的布设位置,给出如图 1所示的5种测站布局示意图,图中黑色星号表示测站节点。测站节点坐标如表 1所示,具体布设方案如下。
 |
| 图 1 5种方案测站布设示意图 Fig.1 Layout of Positioning Sensors in Five Ways |
| 表 1 测站节点坐标 Tab.1 One Sample of Positioning Sensors Coordinates |
 |
方案1:将测站布设在室内的上平面4个角以及室内上平面对角线中心处(测站分布在同一平面上),这也是室内定位系统应用和研究中普遍使用的测站布设方法[10]。
方案2:测站依然布设在室内上平面(测站处于同一平面),将方案1中4个角处的测站分别向里移动至如图 1方案2所示位置。
方案3:在方案1的基础上,将4个角处的测站分别向下移动至如图 1方案3所示位置(测站不在同一平面)。
方案4:在方案2的基础上,将其中4个测站分别布设至如图 1方案4所示位置,有一个测站依然在室内上平面对角线中心处(测站不在同一平面)。
方案5:在方案4基础上将测站节点之间构成的几何体体积进一步增大,是对方案4的进一步优化(测站不在同一平面)。
2.2 DOP数值分析根据DOP理论模型及§2. 1中前4种方案的具体测站坐标值,在图 1模拟的仿真区域,从左下角的坐标原点处开始以0. 1 m为步长(接收机位置)遍历整个仿真区域,针对前4种方案,分别计算GDOP、PDOP、HDOP以及VDOP。仿真结果如图 2~图 5所示,图中红点表示测站节点平面位置。
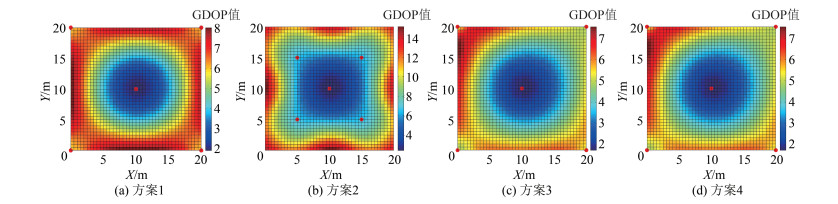 |
| 图 2 4种方案GDOP值分布 Fig.2 GDOP Distributions for Layout of Positioning Sensors in Four Ways |
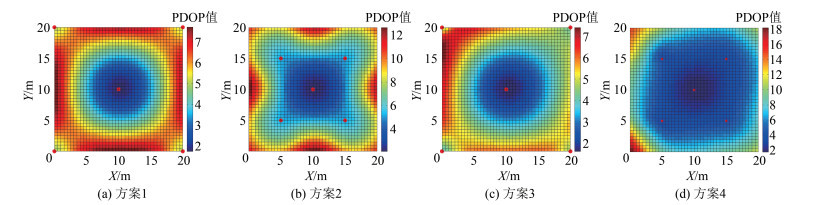 |
| 图 3 4种方案PDOP值分布 Fig.3 PDOP Distributions for Layout of Positioning Sensors in Four Ways |
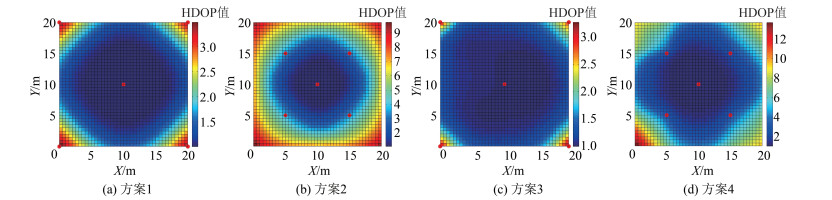 |
| 图 4 4种方案HDOP值分布 Fig.4 HDOP Distributions for Layout of Positioning Sensors in Four Ways |
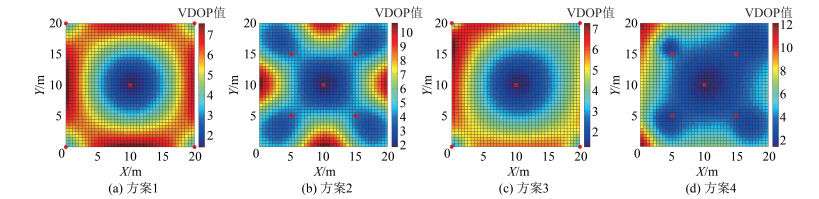 |
| 图 5 4种方案VDOP值分布 Fig.5 VDOP Distributions for Layout of Positioning Sensors in Four Ways |
从图 2可以看出,4种方案仿真区域边缘处的GDOP值偏大。从整体GDOP值来看,方案4优于其他3种方案,尽管方案4在墙角处出现了较大的GDOP值,最大值为21. 559 2。在实际室内环境中,靠近四周的空间里多摆放室内物件,人员活动相对集中于室内环境中部或距离四周墙壁一定距离的空间[20]。从图 3中可以得出,当测站布设在4个角时,PDOP分布呈现圆形快速增大(方案1和方案3),对比方案1和方案3,方案1增大的更剧烈,原因在于方案1测站全部位于同一水平面,而方案3测站间构成几何体,同样,从方案2和方案4的PDOP值可以看出,当测站分布在不同平面(测站间构成几何体)时会得到更好的PDOP值。如果从PDOP角度布设测站节点,为了得到更好的定位精度,不应该将测站节点布设在同一平面,尽可能不要布设在4个墙角处。
对比图 2和图 3发现,前4种方案GDOP和PDOP的整体分布趋势一致,只是局部稍有不同,PDOP整体特征值低于GDOP,其原因和上述GDOP值的结果分析一致,测站节点合理的布设使得GDOP和PDOP值有很大的改善,更好的测站布局可以增强定位精度。
从图 4可以看出,如果仅从HDOP的角度去考虑,方案3为最优方案,方案1次之,方案2是最差的。对比方案1和方案3,唯一不同之处在于测站节点高度设置不一致,实验结果证明,当测站节点布设在不同平面(测站节点构成几何体),会得到更好的HDOP值分布;对比方案1和方案2,即使测站节点布设于同一平面,测站之间的间距适当增大,将会改善HDOP值的分布;对比方案2和方案4发现,在测站节点不在同一平面时(测站节点构成几何体),HDOP值的分布亦会改善;对比分析方案3和方案4(各测站节点高程一致)发现,在测站节点布设在不同平面时,测站节点之间构成的几何体的体积越大,则HDOP值越小,定位精度越高。通过上述实验对比分析,测站节点布设在同一平面,测站节点之间距离在有效信号范围内尽可能的大,将会改善HDOP值分布;在测站节点不设在同一平面时,测站节点之间构成的几何体体积越大,HDOP值分布会更优。当然,在实际应用场景中,不仅仅从HDOP的角度去考虑测站布设,比如还要考虑无线信号的多径传播、非视距传播以及人员扰动等一系列问题。
从图 5可以看出,在测站节点正下方区域,VDOP值呈现出较小的分布值。当测站节点布设在室内4个角处时(方案1和方案3),VDOP呈现圆形增大,与GDOP、PDOP分布值是一致的(见图 2和图 3)。4种方案中,方案4尽管在局部(靠近墙角处)出现了较大的VDOP值,但整体VDOP值分布中是最优的。当测站均布设在同一水平面上时(方案1和方案2),VDOP分布值均不理想,当测站布设在不同水平面时,VDOP值有所改善。
从图 2~图 5可以发现,尽管方案4从全局的角度看在4种方案中得到的DOP值最优(除HDOP),但是由于在该方案的布局在墙角处出现了较大的DOP值,需要进一步优化,可在方案4的基础上,保持各个测站高程不变,测站节点向外移动至如表 1方案5所示坐标位置(见图 1),扩大测站节点构成的几何体的体积,结果表明,DOP值分布进一步得到改善,仿真分析结果如图 6所示。对比分析方案4、方案5可知,GDOP最大值从21. 559 2降低至9. 881 8,PDOP最大值从18. 113 9降低至8. 768 3,HDOP最大值从13. 665 0降低至5. 729 8,VDOP最大值从12. 049 9降低至7. 615 8,其他各项统计特性亦有所改善,说明合理的布设测站有利于提高系统的稳定性,从而增强定位精度以及室内定位完好性。
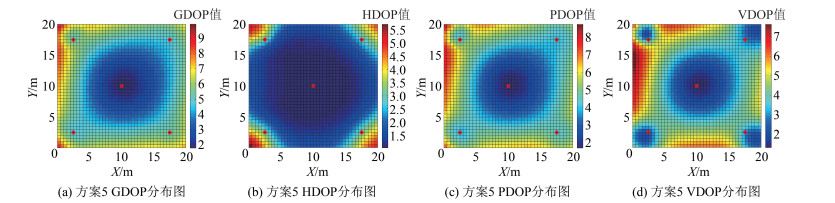 |
| 图 6 方案5DOP值分布图 Fig.6 DOP Distribution for Layout of Positioning Sensors in the Fifth Way |
3 结束语
DOP度量了测站节点结构特征对定位精度的影响。本文设计了5种方案,在每一种方案下,改变待测节点(用户接收机)的位置计算获得DOP分布值,实验表明,在WiFi测站节点数目一定的情况下,当测站节点布设在同一水平面时,GDOP、PDOP、HDOP和VDOP均出现较差的分布值,当测站节点不在同一平面(测站节点之间构成几何体),上述DOP值均有所改善,并且几何体体积越大,DOP值越小,这意味着在测距精度一定的情况下,合理的布设测站可以提高定位精度。
此外,本文实验针对5个WiFi测站节点以及在20 m×20 m×3 m的室内空间展开,设计了5种数值分析方案,但在实际情况中,往往存在更大更复杂的室内空间,比如大型商场、大型体育馆、展览馆等,因此本研究存在一定的局限性,下一步研究可将区域面积增大,WiFi测站节点数目增多,增加实测环节,进行仿真与实测的对比分析,检验本文的研究结果。
| [1] |
陈锐志, 陈亮. 基于智能手机的室内定位技术的发展现状和挑战[J]. 测绘学报, 2017(10): 118-128. |
| [2] |
陈锐志, 叶锋. 基于WiFi信道状态信息的室内定位技术现状综述[J]. 武汉大学学报·信息科学版, 2018, 43(12): 2 064-2 070. |
| [3] |
Bahl P, Padmanabhan V N. RADAR: An in Building RF-Based User Location and Tracking System[C]. INFOCOM 2000. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies, Tel Aviv, Israel, 2000
|
| [4] |
吴伟, 花向红, 吴帮, 等. 基于WiFi信号的整体区间重叠度的AP选取算法[J]. 测绘地理信息, 2021, 46(2): 67-70. |
| [5] |
Youssef M, Agrawala A. The Horuslocation Determination System[J]. Wireless Networks, 2008, 14(3): 357-374. DOI:10.1007/s11276-006-0725-7 |
| [6] |
殷富成, 吴栋, 王艳, 等. 基于WiFi的混合定位算法研究[J]. 系统仿真学报, 2016(12): 2 879-2 886. |
| [7] |
Li L C, Ran C S, Wei F. An Enhanced Genetic Algorithm for the Nonlinear Optimization in TDOA-Based Location[J]. Systems Engineering and Electronics, 2003, 25(8): 971-973. |
| [8] |
赵海, 张宽, 朱剑, 等. 基于TDOA的超声波测距误差分析与改进[J]. 东北大学学报(自然科学版), 2011, 32(6): 802-805. DOI:10.3969/j.issn.1005-3026.2011.06.011 |
| [9] |
甄杰, 吴建新, 刘纪平, 等. 一种单基站高精度室内应急定位方法[J]. 武汉大学学报· 信息科学版, 2020, 45(8): 1 146-1 154. |
| [10] |
彭逸凡, 李广云, 王力. UWB室内定位测站布设PDOP值分析[J]. 导航定位学报, 2017, 5(2): 103-106. |
| [11] |
侯全武, 王坚, 胡洪, 等. 传感器位置对狭长空间定位精度的影响[J]. 大地测量与地球动力学, 2013, 33(1): 117-122. |
| [12] |
高虎, 俞志强. 基于四站时差定位原理的星型布站分析[J]. 空军雷达学院学报, 2004, 18(3): 22-24. |
| [13] |
杨开伟, 黄劲松. 卫星导航系统定位精度评估[J]. 海洋测绘, 2009, 29(4): 26-28. |
| [14] |
Richard B, Langley R B. Dilution of Precision[J]. GPS World, 1999, 22: 52-59. |
| [15] |
王雪延. 基于UWB基站配置的室内定位研究[D]. 西安: 西安电子科技大学, 2014
|
| [16] |
李玲玲. 高精度室内定位系统伪卫星布局研究[D]. 哈尔滨: 哈尔滨工业大学, 2015
|
| [17] |
周忠谟, 易杰军. GPS卫星测量原理与应用[M]. 北京: 测绘出版社, 1992.
|
| [18] |
Tiwary, K, Sharada G. Improving GDOP in Pseudolite only Navigation System Using Genetic Algorithm[J]. International Journal of Research in Computer and Communication Technology, 2013, 2: 392-399. |
| [19] |
戴超. 室内伪卫星实时定位技术及其实现[D]. 上海: 上海交通大学, 2014
|
| [20] |
唐兆鹏, 花向红, 王华强, 等. WiFi室内定位的不同接入点选取策略的性能评估分析[J]. 测绘地理信息, 2019, 44(3): 73-76. |
 2022, Vol. 47
2022, Vol. 47

