| 空域和频域相结合的矢量空间数据多重盲水印算法 |
2. 甘肃省地理国情监测工程实验室,甘肃 兰州,730070;
3. 兰州市勘察测绘研究院,甘肃 兰州,730050
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China;
3. Lanzhou City Survey Mapping Institute, Lanzhou 750050, China
矢量空间数据在城市管理、交通旅游、环境保护、国防安全等方面发挥着非常重要的作用,获取通常要借助于昂贵的专业设备和花费大量的人力、物力,所以,其版权保护至关重要。矢量空间数据以数字化的形式保存,在方便数据拷贝和传播的同时,也使盗版变得极其容易。水印技术在数字内容安全、版权保护和认证方面被认为是目前最有前景的技术之一[1]。数字水印是保护数字地图版权的一种有效方法[2],随着地理空间数据安全保护需求的日益增加,水印技术在地理空间数据版权保护方面得到了广泛的重视和研究。
根据水印的嵌入位置,矢量空间数据水印算法可以分为空域水印算法和频域水印算法。空域水印是直接在空间数据上嵌入水印,具有水印容量大、算法简单、对顶点攻击的鲁棒性好等特点[2-4]。频域算法首先把空间数据通过数学变换,如DWT(discrete wavelet transform)[5, 6]、DCT(discrete cosine transform)[7]、DFT(discrete Fourier transform)[8, 9],水印信息嵌入变换后的系数中。这类算法鲁棒性强,大多数能够抵抗几何变换的攻击,但是对顶点攻击有明显的弱势。
目前矢量空间数据鲁棒水印算法大多采用单一水印技术,每一种水印技术都是基于一种算法来实现。矢量空间数据采用单一数字水印技术,往往不能抵抗多种不同类型的攻击。目前为止,没有哪一种水印技术可以抵抗所有的水印攻击。因此,基于多种水印方法的组合,采取不同的水印技术手段,取长补短,进行有效的组合,来防范不同的水印攻击,是行之有效的数字水印研究方向之一。 目前,已有部分学者开始矢量空间数据多重水印算法的研究[10-12]。
1 矢量空间数据多重水印特点分析多重水印是指在同一个载体中以多种方式嵌入多个水印的技术,它将多个水印标识通过多种方式嵌入到载体中,从不同方面提高了水印的鲁棒性和安全性[13]。
矢量空间数据多重水印嵌入中可能存在如下问题: ①多次嵌入水印信息,不论是采用相同或不同的嵌入算法,经过多重水印嵌入后,根据嵌入水印的前后顺序不同,先嵌入的水印很难提取出来; ②在矢量空间数据中嵌入多重水印,将会对原始空间数据造成更大的改变,水印嵌入引起的误差增大; ③多重水印嵌入中,如果算法效率不高,则实用性不强。
就矢量空间数据水印算法而言,空间域算法通常简单、易操作,水印嵌入量较大,能够抵抗增加点、删除点、裁剪等攻击,但抵抗几何攻击、噪声等攻击方面效果较差;某些频域算法刚好相反,频域算法在顶点增加、删除方面鲁棒性差,但在抵抗几何攻击方面又具有很好的优点。综上所述,空域和频域相结合的数字水印算法具有比单重水印明显的优势。
2 一种多重水印嵌入算法多重水印嵌入流程如图 1所示。算法中嵌入两个不同的水印图像见图 2。为了消除水印图像像素之间的相关性,同时增强水印的安全性,水印图像在嵌入之前,应用Logistic混沌算法置乱。混沌变换的初始值可以作为水印信息提取的密钥。
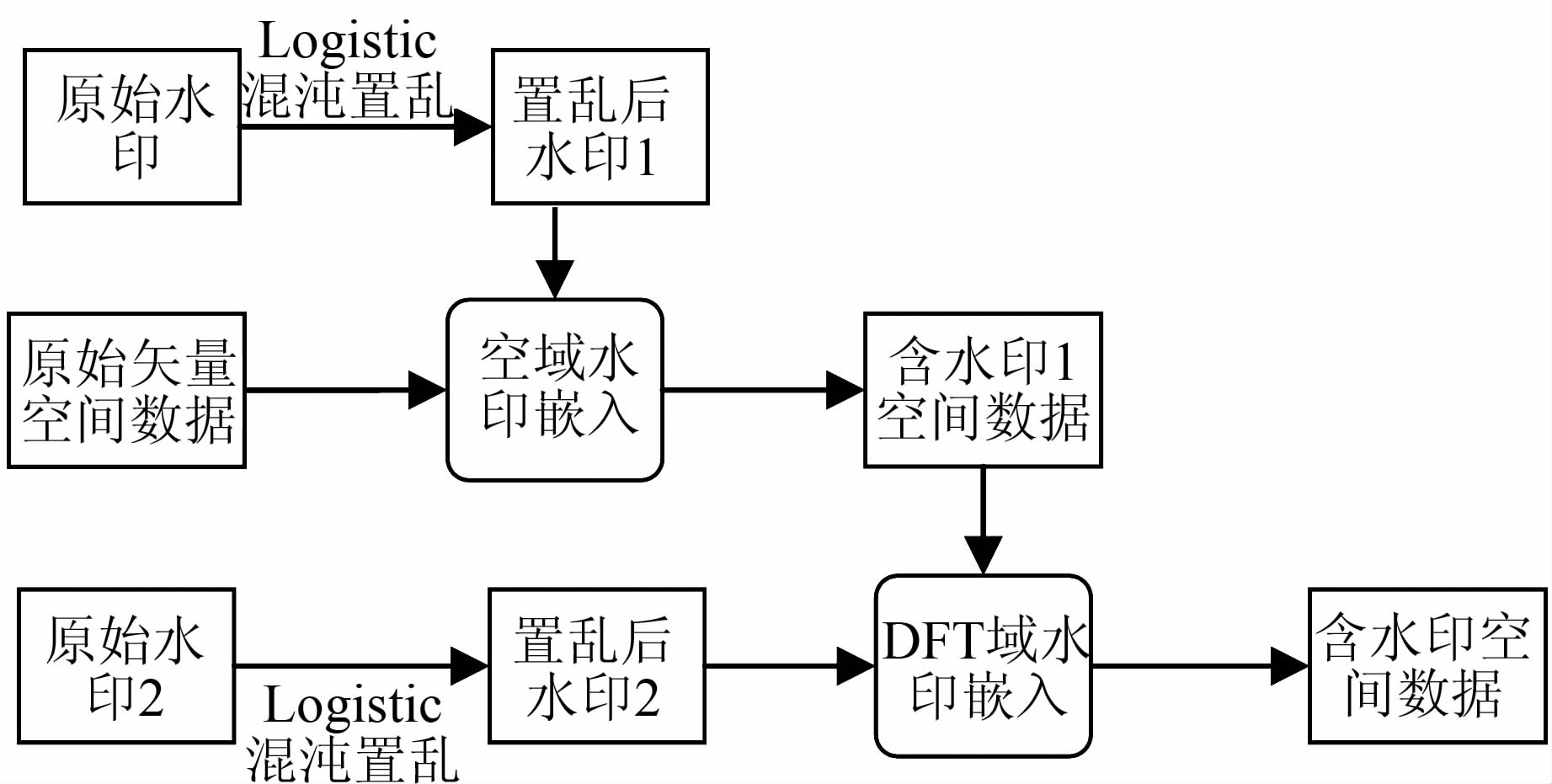 |
| 图 1 多重水印嵌入流程图 Figure 1 Flowchart of Multiple Watermarks Embedding |
 |
| 图 2 原始水印 Figure 2 Original Watermark |
2.1 空域水印嵌入算法
本算法以图形要素为单位嵌入水印1。具体嵌入算法流程如下:
1) 读取矢量地理空间数据,提取坐标点的X、Y值,提取空间数据坐标值中高位有效位部分,记为ix、iy;
2) 计算Hash(ix)和Hash(iy)的值i,Hash()函数为坐标点与水印比特之间的哈希映射函数,i是水印的位置;
3) 提取该坐标点需要嵌入的水印位w[i](1) ,w为置乱后的水印,M为水印的长度;
4) 通过QIM (quantization index modulation)方法,在顶点坐标值中嵌入水印,R为量化值,以X坐标值为例,此时分两种情况进行讨论: ①如果w(i)=0 并且MOD(x,R)>R/2,则 x=x-R/2; ②如果w(i)=1 并且MOD(x,R)≤R/2,则 x=x+R/2;
5) 依次对该要素所有坐标点的X、Y值嵌入水印。
2.2 DFT域水印嵌入算法在空域水印嵌入完成后,以含水印1的空间数据为载体,同样以图形要素为单位,再次嵌入水印2。具体嵌入算法流程如下:
1) 读取空间数据坐标点,根据式(1) 产生复数序列{ak}:
| $~{{a}_{k}}={{x}_{k}}+i{{y}_{k}}~\left( k=1,\ldots ,N \right)$ | (1) |
其中,xk、yk为顶点坐标值;N为图形要素顶点数目。
2) 对序列{ak}进行DFT变换,得到变换后的DFT系数{al}。该序列包括幅度系数{|Al|}和相位系数{∠Al};
3) 应用QIM量化方法,水印嵌入到幅度系数{|Al|}和相位系数{∠Al}。通过式(2) 计算得出嵌入水印后的系数A′l:
| $A{{'}_{l}}=\left\{ \begin{align} & {{A}_{1}}-R/2,if~w\left( i \right)=0且MOD\left( {{A}_{1}},R \right)>R/2 \\ & {{A}_{1}},if~w\left( i \right)=0且MOD\left( {{A}_{1}},R \right)\le R/2 \\ & {{A}_{1}}+R/2,if~w\left( i \right)=1且MOD\left( {{A}_{1}},R \right)\le R/2 \\ & {{A}_{1}},if~w\left( i \right)=1且MOD\left( {{A}_{1}},R \right)>R/2 \\ \end{align} \right.$ | (2) |
4) 对{A′l}进行离散傅里叶逆变换,得到嵌入水印后的复数序列{a′k};
5) 根据序列{a′k}修改相应顶点坐标,得到嵌入水印后的矢量数据;
6) 输出保存含水印矢量空间数据。
两种算法中都应用到了QIM量化方法嵌入水印。前者水印嵌入到坐标值中,后者水印嵌入到DFT变换系数中。载体数据和水印比特之间映射都是通过Hash(x)=x%M+1函数计算,为了使Hash函数的值均匀介于1~M之间,可以适当放大坐标值或变换系数,再计算映射值。
通过QIM量化方法嵌入水印时,如果直接量化嵌入,则水印就会嵌入数据的整数位部分,会导致数据误差太大。在水印嵌入之前,通过放大数据,然后量化嵌入,再缩小相应倍数。这样就会使水印嵌入到数据的小数位部分,大大减小水印嵌入引起的误差。
试验对R取值在50、100、150、200下,都可以很好地提取水印。当R<50或R>200时,提取到的水印效果较差;当R太小,量化提取区间不明显;当R较大时,变换域水印中系数修改较大,逆变换后的坐标数据也会发生较大的改变,提取水印效果较差。
2.3 水印提取算法水印提取是水印嵌入的逆过程。由于采用不同的算法嵌入了不同的水印,因此两个水印应分别提取。
空域水印提取过程如下:
1) 读取待测数据,提取坐标点的X、Y值,提取空间数据坐标值中高位有效位部分,记为ix、iy;
2) 通过Hash()函数,计算出水印的位置i;
3) 通过QIM量化方法提取水印位w(i)的值,R取嵌入水印时的量化值;
4) 对提取到的一维水印序列进行升维处理并反置乱,得到最终水印图像。
DFT域水印提取过程如下:
1) 读取待测数据,读取空间数据坐标点,根据式(1) 产生复数序列{a′k};
2) 对序列{a′k}进行DFT变换,得到离散傅里叶系数{A′i};
3) 对{A′i}的幅度系数和相位系数分别放大10n倍,采用嵌入水印时的量化值R,计算出系数所在的量化区间,各自提取出幅度系数水印和相位系数水印;
4) 对提取到的两个一维水印序列,变换为二维图像并反置乱,得到最终水印图像。
在两个水印算法中,每一个水印都被多次嵌入,因此采用投票原则来确定水印信息。计算方法是:定义一个与水印序列等长的整数序列{B(i)=0,i=1,…,M},M为水印长度。单个水印位b′(i)={1,-1},相同水印位提取过程中,使用公式B(i)= B(i)+b′(i)来统计出水印信息值-1和1的多数,如“1”为多数,则B(i)>0;然后根据公式(3) 来重构出二值水印图像。
| $w\prime \left( i \right)=\left\{ \begin{align} & 1,\text{if}B\left( i \right)>0 \\ & 0,\text{if}B\left( i \right)\le 0 \\ \end{align} \right.$ | (3) |
试验选用一幅1∶5 000的界线图,数据格式为ArcGIS的shp格式。该图有594个图形对象,共有20 292个坐标点。对嵌入水印后的数据进行了误差统计,并从水印的不可见性及鲁棒性进行了分析。试验中两个水印都是32像素×64像素的二值水印图像,如前述图 2(a)、2(b)所示。图 2(c)是水印1混沌置乱后的水印图像。
3.1 误差及不可见性分析本文采用均方根误差(RMSE)和最大误差等指标评价水印嵌入对矢量数据精度的影响大小。统计结果如表 1所示。
| 表 1 均方根误差和最大误差统计表 Table 1 Statistics of RMSE and Maximum Error |
 |
RMSE=
从表 1中可以看出,嵌入水印所引起的均方根误差为5.015 4×10-4,最大误差为8.861 6×10-4,75%的数据误差小于6×10-4。尽管采用两种方法独立嵌入多重水印,但嵌入水印后引起的数据误差较小,完全在数据精度要求之内,可见该算法不会影响数据的使用。
通过对水印嵌入前后数据可视化叠加对比,并局部放大显示如图 3所示。从图中可以看出水印嵌入前后视觉上没有明显的差别。从表 1的误差分析数据来看,水印嵌入引起的最大误差及RMSE都很小,因此,水印具有很好的不可见性。
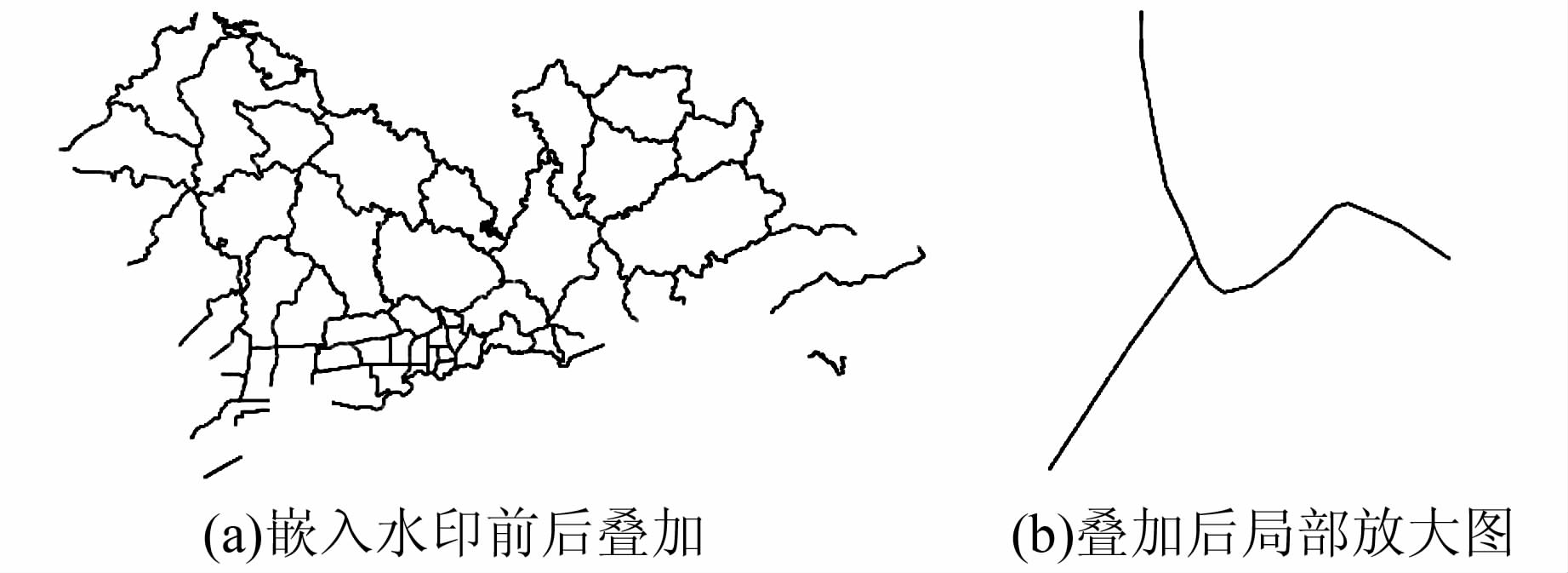 |
| 图 3 可视化比较 Figure 3 Visualization Comparison |
3.2 水印的鲁棒性分析
对提取到的水印图像与原始水印图像通常是用相关系数来评价其相似性的,计算公式如式(4):
| $NC=\frac{\sum\limits_{i=1}^{m}{\sum\limits_{j=1}^{N}{\text{XNOR}\left( W\left( i,j \right),W\prime \left( i,j \right) \right)}}}{M\times N}$ | (4) |
式中,M×N表示水印图像的大小;W(i,j)表示原始水印信息;W′(i,j)表示提取的水印信息;XNOR表示异或非运算。
3.3 增加点、修改点及裁剪攻击从表 2中可知,对含水印数据增加顶点2倍多后,依然能够很好地提取水印1。这是由于空域算法能够很好地抵抗顶点攻击。增加顶点后,并不影响原来数据的水印信息。但是对于水印2,由于DFT具有局部性的特点,顶点的增加及修改都会导致DFT域系数较大的变化,无法提取水印2。对矢量数据的裁剪试验结果表明,裁剪后,从剩余要素中依然能够较好地提取两个水印信息。
| 表 2 増、删点及裁剪攻击的鲁棒性 Table 2 Robustness of Vertex Insertion and Removal,Cropping Attacks |
 |
3.4 压缩及要素删除攻击
从表 3可以看出,对含水印数据进行D-P压缩试验,取阈值5,压缩至9 239个顶点后,能很好地提取水印1,但无法提取水印2;而对于要素删除攻击,从表 3可以看出,即使删除50%要素后,依然能够很好地提取所有水印。在该算法中,每一个水印都被多次嵌入各自的域空间,而且水印信息均匀地分布在每一个要素。因此,部分要素的删除不会对水印信息造成太大的破坏。
| 表 3 压缩、要素删除攻击的鲁棒性 Table 3 Robustness of Compression,Delete Elements Attacks |
 |
3.5 几何攻击
由表 4可知,在经过旋转、平移、缩放攻击后,水印2的提取基本不受影响。这是由于水印2是嵌入傅里叶变换后的系数中,傅里叶变换的幅度系数对旋转操作不受影响,而傅里叶变换的幅度系数和相位系数均不受平移操作的影响。因此,水印对几何变换中的攻击具有很好的鲁棒性。而对于水印1,水印是直接嵌入空间数据坐标值中,由于几何变换后,空间数据坐标值发生了变化,因此无法提取水印。
| 表 4 几何攻击的鲁棒性 Table 4 Geometric Attacks Robustness |
 |
3.6 乱序及格式转换攻击
本文对坐标排序、要素排序攻击进行了试验。在该算法中,水印的嵌入不依赖于坐标点顺序及要素顺序,因此,两个水印的提取都不受影响。当含水印的矢量空间数据从一种格式转换成另一种矢量空间数据格式后,无法直接提取水印信息,需要转换到原来的矢量数据格式后,才可以提取水印信息。两种不同数据格式的矢量空间数据在进行格式转换时,由于两者数据结构、存储方式、单位、精度等的差异,转换后的数据会产生微小的差异,这个差异对水印信息的提取影响很小。
3.7 水印嵌入顺序的影响本算法中多重水印的嵌入顺序是先在空域嵌入水印,后在DFT域嵌入水印。试验中,空域水印通过控制嵌入到坐标数据小数点后4、5位部分,在变换域水印嵌入中,通过放大系数的方法控制水印嵌入到小数点后7、8位部分,这样第2个水印的嵌入不会覆盖或影响第1个水印。而如果颠倒嵌入顺序,即先嵌入DFT域水印、后嵌入空域水印,则空域水印会对DFT域水印造成很大的影响,先嵌入的DFT域水印无法提取。
4 结束语本文采用空域和DFT域算法相结合的水印算法,两种水印算法取长补短,克服了单重水印抗攻击能力弱的缺点,提高了水印的整体抗攻击能力。空域水印对顶点增加、压缩、顶点修改、噪声等攻击优势明显;DFT域水印具有很好地抵抗几何攻击的能力。同时两种算法对裁剪、要素删除、乱序、数据格式转换抗攻击能力强。试验结果表明,该算法具有很好的不可见性,水印嵌入误差小。两种水印都采用盲水印,具有很好的实用性。然而该算法不能抵抗某些复合攻击,这将是本文的后续研究工作。
| [1] |
朱长青, 许德合, 任娜, 等.
地图空间数据数字水印理论与方法[M]. 北京: 科学出版社, 2014 .
Zhu Changqing, Xu Dehe, Ren Na, et al. Watermarking Theory and Methods for Map Spatial Data[M]. Beijing: Science Press, 2014 . |
| [2] |
胡祺, 王芙蓉, 郭丙轩, 等. 地理空间数据安全技术研究与实现[J].
测绘信息与工程,2011,36(4) : 49–51.
Hu Qi, Wang Furong, Guo Bingxuan, et al. Security Technology for Geo-Spatial Data[J]. Journal of Geomatics,2011,36(4) : 49–51. |
| [3] |
贾培宏, 马劲松, 史照良, 等. GIS空间数据水印信息隐藏与加密技术方法研究[J].
武汉大学学报·信息科学版,2004,29(8) : 747–750.
Jia Peihong, Ma Jinsong, Shi Zhaoliang, et al. Technical Methods for Encrypting and Hiding Digital Watermark in GIS Spatial Data[J]. Geomatics and Information Science of Wuhan University,2004,29(8) : 747–750. |
| [4] |
马桃林, 顾翀, 张良培. 基于二维矢量数字地图的水印算法研究[J].
武汉大学学报·信息科学版,2006,31(9) : 792–794.
Ma Taolin, Gu Chong, Zhang Liangpei. Watermarking Algorithm on 2D Vector Digital Maps[J]. Geomatics and Information Science of Wuhan University,2006,31(9) : 792–794. |
| [5] | Kitamura I, Kanai S, Kishinami T. Digital Watermarking Method for Vector Map Based on Wavelet Transform[C]. Proc of Annual Conference of the Geographic Information Systems Association, Tokyo, Japan, 2000 |
| [6] |
李媛媛, 许录平. 矢量图形中基于小波变换的盲水印算法[J].
光子学报,2004,33(1) : 97–100.
Li Yuanyuan, Xu Luping. Vector Graphical Objects Watermarking Scheme in Wavelet Domain[J]. Acta Photonica Sinica,2004,33(1) : 97–100. |
| [7] | Voigt M, Bian Y, Busch C. Reversible Watermarking of 2D-Vector Data[C]. Proceedings of the 2004 Workshop on Multimedia and Security, ACM, Magdeburg, Germany, 2004 |
| [8] | Vassilios S, Nikolaidis N, Pitas I. Fourier Descriptors Watermarking of Vector Graphics Images[C]. International Conference on Image Processing, Hong Kong, China, 2000 |
| [9] |
王奇胜, 朱长青, 许德合. 利用DFT相位的矢量地理空间数据水印方法[J].
武汉大学学报·信息科学版,2011,36(5) : 523–526.
Wang Qisheng, Zhu Changqing, Xu Dehe. Watermarking Algorithm for Vector Geo-spatial Data Based on DFT Phase[J]. Geomatics and Information Science of Wuhan University,2011,36(5) : 523–526. |
| [10] |
车森, 邓术军. 基于双重网格的矢量地图数字水印算法[J].
海洋测绘,2008,28(1) : 13–17.
Che Sen, Deng Shujun. Watermarking Arithmetic of 2D Vector Maps Based on Two-tier Grids[J]. Hydrographic Surveying and Charting,2008,28(1) : 13–17. |
| [11] |
孙建国, 门朝光, 张国印. 抗解释攻击的矢量地图静态双重水印[J].
哈尔滨工程大学学报,2010,31(4) : 488–495.
Sun Jianguo, Men Chaoguang, Zhang Guoyin. Static Dual Watermarking of Vector Maps to Anti-Interpretation Attacks[J]. Journal of Harbin Engineering University,2010,31(4) : 488–495. |
| [12] |
李强, 闵连权, 何宏志, 等. 一种多重水印嵌入的解决方案研究[J].
测绘科学,2011,36(2) : 119–120.
Li Qiang, Min Lianquan, He Hongzhi, et al. A Solution Research on Multiple Watermark Embedding[J]. Science of Surveying and Mapping,2011,36(2) : 119–120. |
| [13] | 鲁芳. 多重文本数字水印技术的研究[D]. 长沙:湖南大学, 2005 11111Lu Fang. Research on Multiple Text Digital Watermark Technology[D]. Changsha: Hunan University, 2005 |
 2016, Vol. 41
2016, Vol. 41