| 一种基于SIFT-NMI的多源影像配准方法 |
遥感影像配准是后续影像处理过程的基础和前提[1],利用有效的特征点,如尺度不变特征变换(scale invariant feature transform, SIFT)进行配准是最常用的一种方法[2, 3]。目前针对同源影像的配准技术已经十分成熟,但多源影像配准问题还有很大的研究空间,原因在于多源影像间的光谱、分辨率等差异明显,这一方面会增加特征点提取的难度,另一方面特征点的分布和数量也变得不稳定[4]。针对这些问题,目前已经有了一些研究。文献[5]引入相位一致性特征有效抵抗了影像间的辐射差异,提高了匹配性能。文献[6]利用Harris[7]特征点和互信息[8]方法进行多源影像配准,能提取数量众多的特征点,同时对光谱差异不敏感。文献[9-11]通过对SIFT进行改进使特征点分布更均匀,提高了影像配准精度。文献[12, 13]对互相关方法进行改进,实现了红外和可见光图像配准。
针对多源影像配准问题,当前常用方法有两类:一类是基于特征点的方法;一类是基于域的方法。两类方法各有优劣:前者有众多成熟的算子,配准速度快,但是特征点数量和分布往往难以控制;后者对光谱差异不敏感,但随着图像尺寸增大,计算效率低下[14],不适合大幅遥感影像配准。因此,本文提出一种SIFT-NMI配准方法。首先用SIFT进行粗配准,再使用归一化互信息[15]进行精配准,可以得到数量充足、分布均匀的匹配点,实现多源影像自动配准。
1 配准技术方法 1.1 技术流程本文配准技术分为粗配准和精配准两个流程,其方法技术路线如图 1所示。
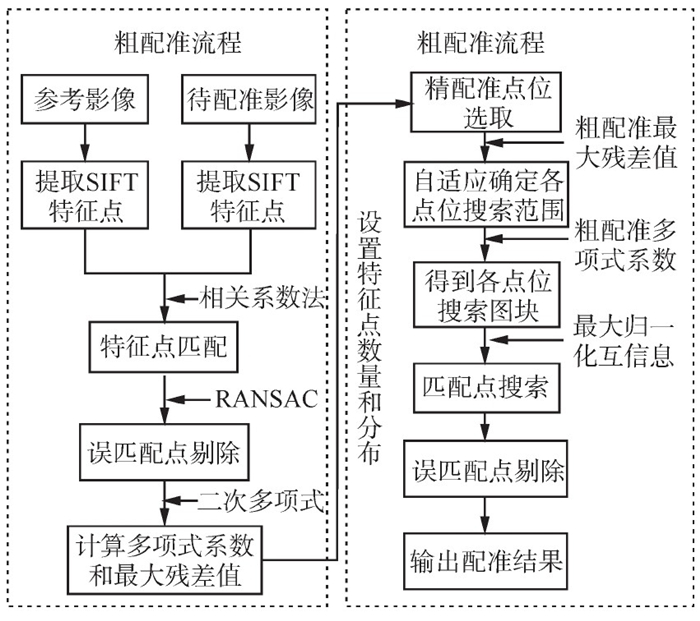 |
| 图 1 技术流程 Fig.1 Technical Flow Chart |
1.2 关键技术 1.2.1 归一化互信息
归一化互信息(normalized mutual information, NMI)常用于度量两个聚类结果的相似程度,是从互信息基础上发展而来。在图像配准当中,将参考影像和待配准影像的灰度值当作两个随机变量A和B,用PA(a)、PB(b)分别表示A、B的概率密度函数,PAB(ab)表示A、B的联合概率密度函数,则A和B的互信息可表示为:
| $ I(A, B)=H(A)+H(B)-H(A, B) $ | (1) |
式中,H(A)、H(B)和H(A, B)分别代表随机变量A, B的个体熵和联合熵,理论上当两幅影像完全配准时互信息达到最大。
| $ \left\{ {\begin{array}{*{20}{c}} {H(A) = \sum\limits_a - {P_A}(a)\lg {P_A}(a)}\\ {H(B) = \sum\limits_b - {P_B}(b)\lg {P_B}(b)}\\ {H(A, B) = - \sum\limits_a {\sum\limits_b {{P_{AB}}} } (a, b)\lg {P_{AB}}(a, b)} \end{array}} \right. $ | (2) |
但使用互信息配准也存在问题[16, 17]:受插值等因素的影响,图像的互信息值不是一条平滑的曲线,而存在较多的局部极值,这些极值会影响配准速度。因此有学者将NMI作为评价配准结果的指标,NMI的优点是比互信息更加准确,其表达式如下:
| $ \operatorname{NMI}(A, B)=\frac{H(A)+H(B)}{H(A, B)} $ | (3) |
按照上式进行计算的归一化互信息的取值范围是[1,2],数值越大表示图像配准结果越好。
1.2.2 基于SIFT-NMI的配准方法SIFT优点众多,因而广泛应用在遥感影像特征提取当中[18]。为克服尺度差异影响,本文粗配准阶段使用SIFT特征。粗配准具体步骤为:①为了能够提取更多特征点,配准前对两幅影像进行Wallis[19]变换,然后同时提取SIFT特征点。②构建影像金字塔,在不同尺度影像上使用相关系数法搜索匹配点。③当尺度空间达到原始影像层后,利用最小二乘法[20]进行特征点精匹配。④接着利用随机抽样一致算法(random sample consensus, RANSAC)进行误匹配点剔除,进而得到精确匹配点。
粗配准结束后,为了克服光谱差异影响,利用NMI进行精配准。再以粗配准数据为基础,可保证控制点数量充足、分布均匀。精配准具体步骤为:①选取控制点。在参考影像上选点,设置参数为两个控制点间宽和高的步长(单位:像素),步长越长,控制点数量越少、分布越稀疏。②确定搜索范围。控制点选取结束后,需要搜索匹配点坐标,搜索范围是两倍的粗配准阶段最大残差绝对值。③匹配点搜索。根据粗配准变换系数将控制点映射到待配准影像,进行图块(Block)-图块(Block)匹配,最后以NMI最大值确定匹配Block,进而确定匹配点。④先以NMI值作为约束条件,剔除匹配点中值较小的一系列点(剔除阈值由人为设定),再根据最小二乘法剔除残差值较大的点,然后使用RANSAC方法进行剔除,用最终剩下的匹配点进行二次多项式拟合,结合双线性重采样输出配准结果。
2 配准实验与分析 2.1 定性分析实验数据为无人机可见光、近红外和红边影像。可见光影像大小为7 952×5 304像素,地面分辨率1.6 cm;其他两个波段影像大小为1 280×960像素,地面分辨率8.3 cm。选取两个区域进行实验,区域1、区域2的待配准影像分别是近红外、红边影像,配准时以可见光影像为参考。因计算NMI需要,故将可见光影像转换为灰度图显示。
图 2背景是可见光影像,中央分别是近红外影像和红边影像。为方便观察,对配准中间结果图重采样为相同大小并截取局部图像进行显示,如图 3、图 4所示。
 |
| 图 2 可见光和近红外、红边影像对比图 Fig.2 Images of Visible and Near-Infrared, Red Edge Band |
 |
| 图 3 区域1和区域2粗配准特征点分布情况 Fig.3 Distribution of Coarse Registration Feature Points in Region 1 and Region 2 |
 |
| 图 4 区域1和区域2精配准控制点分布情况 Fig.4 Distribution of Precision Registration Control Points in Region 1 and Region 2 |
虽然使用NMI匹配Block的方法能有效克服光谱差异影响,但需要注意的是,匹配地面控制点要比树冠控制点更准确,因为地物的高低起伏会影响配准,卫星遥感影像由于高度很高,可看作正射影像,高差影响不大,而无人机飞行高度较低,地形起伏不能忽略,因此高差也容易带来更大的误差。另外,因参考影像控制点以规则格网点设置,故在误匹配点剔除阶段仍会剔除一部分控制点。
为验证本文方法,使用上文粗配准阶段的SIFT+RANSAC方法与本文方法作比较,结果如表 1、图 5、图 6所示。其中表 1中1、2代表实验区域,SR代表SIFT+RANSAC方法,SN代表本文SIFT-NMI方法。
| 表 1 SIFT+RANSAC方法与本文方法各项指标 Tab.1 Index of SIFT+RANSAC and Proposed Method |
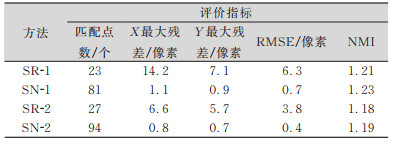 |
 |
| 图 5 区域1 SIFT+RANSAC方法和局部与本文方法和局部配准结果 Fig.5 SIFT+RANSAC Method and Local Image and Proposed Method and Local Image Registration Result of Region 1 |
 |
| 图 6 区域2 SIFT+RANSAC方法和本文方法配准结果 Fig.6 SIFT+RANSAC Method Local and Proposed Method Local Registration Result of Region 2 |
2.2 定量分析
本文配准结果的定量分析,将从匹配点数量、坐标残差、RMSE和NMI这4个方面进行。
NMI参见式(3),坐标残差和RMSE计算公式如式(4)、式(5)所示:
| $ \left\{\begin{array}{l} \Delta x_i=x_i-\hat{x}_i \\ \Delta y_i=y_i-\hat{y}_i \end{array}\right. $ | (4) |
式中,Δxi、Δyi为坐标残差;xi、yi为匹配点图像坐标;
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(\Delta x_i\right)^2+\left(\Delta y_i\right)^2} $ | (5) |
式中,N为参与计算的匹配点数量;Δxi、Δyi为坐标残差。坐标残差、RMSE数值越小,NMI数值越大,表示配准结果越好。
同时,无人机多源影像配准除了受光谱、尺度影响外,地形起伏的影响也不能忽略,为了探究地形起伏对无人机影像配准的影响,本文从图 3区域1中选择10个控制点(5个地面点GP, 5个非地面点NGP)为代表进行分析。
由表 2可以看出,本文方法很好地克服了无人机多源影像间尺度和光谱差异,无论在匹配点数量、分布还是精度上都要优于经典的SIFT+RANSAC方法,通过对误匹配点进行多次剔除,使最终参与配准的匹配点对更加精确,从而实现了无人机多源影像的精确。
| 表 2 不同高度匹配点匹配精度 Tab.2 Accuracy of Matching Points in Different Height |
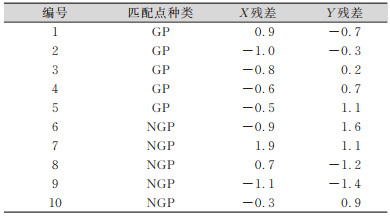 |
从表 2也可以看出,无人机影像上匹配点精度与其所在地物高度有关,地面点精度整体要优于非地面点(如树冠上的匹配点),当影像中地形起伏较大时,难免会影响配准精度。另外,区域1的匹配点数量不如区域2多,配准精度也没有区域2高,再结合图 3中两个区域的原始影像不难看出,区域2整体平坦,地形起伏很小,而区域1大约有1/4被树木所占据,整体起伏较大,实验结果也与分析是一致的。
3 结束语本文针对无人机多源影像配准难点问题,使用SIFT-NMI方法,通过粗-精两步完成了影像间的自动配准。综合利用了基于特征点和基于域两类配准方法的优势,通过两个区域、不同波段影像配准结果进行了定性分析,使用匹配点数量、坐标残差、RMSE和NMI这4项指标对配准结果进行了定量分析。实验结果表明本文方法能有效克服无人机多源影像间尺度、光谱差异影响,在不同影像上都能提取数量充足、分布均匀的匹配点,保证配准的鲁棒性,是一种有效的无人机多源影像配准方法。
但除了尺度和光谱差异,实验结果也表明,地形起伏在无人机多源影像配准中的影响不能忽视,地面点的匹配要比树木、建筑顶端的点更加稳定和准确,因此这个问题仍需进一步研究,从而使无人机多源影像配准更加稳健。
| [1] |
一种改进的相位相关的影像配准方法[J]. 测绘通报, 2011(4): 19-22. |
| [2] |
无人机高光谱内置推扫影像快速拼接方法[J]. 测绘地理信息, 2019, 44(5): 24-28. |
| [3] |
刘鹏飞. 基于SIFT的图像配准方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019
|
| [4] |
利用方向相位特征进行多源遥感影像匹配[J]. 武汉大学学报·信息科学版, 2020, 45(4): 488-494. |
| [5] |
局部相位特征描述的多源遥感影像自动匹配[J]. 武汉大学学报·信息科学版, 2017, 42(9): 1 278-1 284. |
| [6] |
一种利用点特征和互信息的多源遥感影像配准方法[J]. 遥感信息, 2015, 30(3): 99-103. |
| [7] |
Harris和Sift算法在不同尺度下提取特征点分析[J]. 信息系统工程, 2018(8): 161-162. |
| [8] |
Barbara Z, Jan F. Image Registration Methods: A Survey[J]. Image and Vision Computing, 2003, 21(11): 977-1 000. |
| [9] |
Nie X, Zhao R, Jiang Z. A New Image Registration Method for Grey Images[J]. Journal of Electronics, 2004, 21(5): 426-431. |
| [10] |
多源遥感影像配准中的SIFT特征匹配改进[J]. 武汉大学学报·信息科学版, 2013, 38(4): 455-459. |
| [11] |
基于SG-SIFT的光学遥感影像配准[J]. 北京邮电大学学报, 2014, 37(6): 17-22. |
| [12] |
一种结合边缘区域和互相关的图像配准方法[J]. 北京理工大学学报, 2016, 36(3): 320-325. |
| [13] |
陈禾, 周孟哲, 章学静, 等. 一种结合边缘区域和互相关的图像配准方法: CN103714547A[P]. 2014-04-09
|
| [14] |
李良骥. 红外和可见光异分辨率遥感图像配准技术研究[D]. 北京: 中国科学院大学(中国科学院上海技术物理研究所), 2019
|
| [15] |
改进的基于最大归一化互信息的医学图像配准算法[J]. 贵州大学学报(自然科学版), 2008, 25(3): 284-288. |
| [16] |
王云飞. 基于SIFT和归一化互信息的SAR图像配准算法研究[D]. 西安: 西安电子科技大学, 2014
|
| [17] |
王爽, 焦李成, 王云飞, 等. 基于SIFT和归一化互信息的SAR图像配准方法: CN103839265A[P]. 2014-06-04
|
| [18] |
汪道寅. 基于SIFT图像配准算法的研究[D]. 合肥: 中国科学技术大学, 2011
|
| [19] |
改进的Wallis变换在特征提取中的应用[J]. 山东科技大学学报(自然科学版), 2010, 29(6): 34-38. |
| [20] |
基于改进Harris-SIFT算子的快速图像配准算法[J]. 电子测量与仪器学报, 2015, 29(1): 48-54. |
 2022, Vol. 47
2022, Vol. 47

