| 基于货运轨迹数据的城市间货物流动特征分析 |
2. 广东省公共安全与灾害工程技术研究中心,广东 广州,510275;
3. 长沙理工大学交通运输工程学院,湖南 长沙,410114;
4. 广东方纬科技有限公司,广东 广州,510275
2. Guangdong Provincial Engineering Research Center for Public Security and Disaster, Guangzhou 510275, China;
3. School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410114, China;
4. Guangdong Fundway Science and Technology Corporation Limited, Guangzhou 510275, China
城市流动性是发展城市生活和经济环境的一项重要指标,在城市发展中起着关键性作用[1]。城市流动性包括人类移动和货物流动两方面[2]。针对人类移动行为开展的一系列实证研究表明,人类移动具有很强的规律性[3-9],利用重力模型、辐射模型等经典交互模型可以较好地模拟和预测人类在空间上的移动与交互强度[10-12]。不同城市间的货物流动反映了城市间的经济联系和产业互补,对城市的经济发展和产品布局优化具有重要意义。然而,由于货运相关数据获取困难,货物流动作为城市系统流动性的另一个方面受到的关注却相对较少。
早期主要基于小规模调查数据进行城市间货物流动研究[13-15],样本较稀疏且时空分辨率较低。而GPS技术的发展为货运物流移动相关研究提供了更精细的时空轨迹数据[16]。目前,基于物流轨迹数据的研究主要包括货物的移动距离分布特征、两地间的货运联系强度分析等。Comendador等[17]利用货车GPS数据分析了西班牙马德里和索里亚两个城市5种不同类型货物的平均移动距离。以食品运输为例,马德里的市内货物运输平均距离为15.3 km,索里亚的市内平均运输距离为20.3 km。相比之下,城市间的货物移动平均距离更大,如Fu等[18]利用货车GPS轨迹,发现从深圳市盐田口岸出发到周边城市的货物平均移动距离在55.7 km左右。在两地间的货运联系强度分析方面,肖作鹏等[19]利用深圳市的货车GPS数据,分析城市内部主要物流节点之间货运联系强度,并基于货运联系强度网络识别出了深圳市主要的物流节点区域与货车流量廊道。
上述研究对货物流动距离和两地之间的物流交互特征进行了探索,但以城市内部的货物流动为主。城市间货物移动距离的分布规律、不同城市间的货运联系强度特征还有待进一步研究。此外,城市间的货运交互强度是否仍可以用经典的空间交互模型如重力模型、辐射模型来模拟和预测?因此,本文以湖南省的货运轨迹数据为例,分析城市间的货物位移特征和货运联系强度特征,利用重力模型和辐射模型这两类经典的空间交互模型和静态人口、国内生产总值(gross domestic product,GDP)统计数据对城市间的货运联系强度进行预测,并探讨这两种模型在预测城市间货运联系强度上的适用性。
1 研究区与数据湖南省地处中国中部,截至2019年底户籍人口数达7 326.62万人,地区生产总值达26 425.78亿元[20]。湖南省共14个市州级行政区,包括长沙市、株洲市、湘潭市、衡阳市、邵阳市、岳阳市、常德市、张家界市、益阳市、郴州市、永州市、怀化市、娄底市和湘西土家族苗族自治州。本文以湖南为研究区,分析省内各城市间的货物流动特征。
本文数据集为湖南省货车运输GPS轨迹数据,时间为2017年1月1日至1月5日,数据超过1.3亿条。每条数据代表某一辆货车在某一时刻的时空位置信息,包括货车ID、GPS点定位时间、经度、纬度和货车运行的瞬时速度。根据货车行驶的速度及停车时间间隔,提取货运车辆装货与卸货的起讫点[2],作为后续实验分析的数据基础。
2 城市间货物流动特征分析 2.1 位移分布特征为探索城市间货运距离的分布特点,本文利用人类移动中常见的位移特征分布函数,如幂律函数、指数截断的幂律函数、指数函数、双峰威布尔函数,对货物起讫点间的距离进行拟合分析。根据提取出的货运车辆装货与卸货的起讫点,计算每一对起讫点间的距离,而后将这些距离依次从0~560 km均等划分为70组。统计每组距离中的货运起讫点对数量及其在整体样本中的频率,得到每组样本出现的概率。如图 1所示,城市间货物流动存在两个频率明显偏高的位移距离,分别在城市内部(20 km左右)和城市间(200 km左右)出现高峰值。这说明城市间的货运不是完全随距离单调递减,而是在整体上呈现两次波动的趋势。
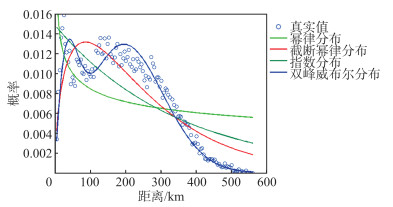 |
| 图 1 位移距离分布拟合 Fig.1 Fitting of Displacement Distribution |
利用上述4种分布函数拟合后的结果为:幂律分布拟合R2=0.27,指数分布拟合R2=0.64,指数截断的幂律分布拟合R2=0.80,双峰威布尔分布的拟合R2=0.92。从图 1中的拟合曲线形状可以发现,指数截断的幂律函数虽然拟合度较高,但低估了在25 km左右的移动距离分布概率,且明显高估了在100 km左右的分布概率。双峰威布尔分布曲线的两个峰值则很好地对应了货运距离的波动特征,具有更好的拟合效果。本文结果与文献[1]中城市内货物流动的距离分布特征相似,表明无论城市内部还是城市间的货物流动,其货物位移更加符合双峰威布尔分布。这与人类移动位移特征中常见的幂律分布和指数分布有较大差异。人类移动往往受距离影响较大,具有明显的距离衰减效应。尤其是长距离的跨城市旅行通常要考虑时间、经济等成本。而货物的供给和流通是经济活动必不可少的一部分,商品贸易的完成必须要有足够的供给来满足消费。因此,货物运输通常是一种不具有弹性或弹性较小的移动行为。为了保障货物及时供给,距离远近对货运物流的影响相对于人类移动大幅降低。
2.2 城市间货运联系强度特征为了探究城市间货物流动的联系强度特征,将货运数据的起讫点矩阵与各城市行政单元结合起来,构建一个空间嵌入式的有向网络G =(N,L)。将研究区内的各个城市根据几何中心抽象成点,记为Ni。两个城市i和j之间的物流联系强度为Lij,其值为由城市Ni流向城市Nj的货运起讫点对总量。
G中每两个城市间的物流联系强度Lij见图 2。可以看出,湖南省内各城市间的货运联系在空间分布上有明显差异,部分城市间存在较强的货运往来,例如,长沙市与周边其他城市(如衡阳市、邵阳市、常德市)的物流联系非常强。而处在研究区外围的城市(如郴州市与永州市、株洲市等)的物流联系相对较弱。联系强度值小于1 000的城市对在整个货运网络中占比达57.1%,说明湖南省各城市间超过半数的货运路线承担了较小流量的运输。联系强度值大于2 500的城市对在整个货运网络中仅占6.6%,即少数城市间的运输路线在湖南省整体物流运输中占主导地位,这些运输路线承担了大量货运流量。
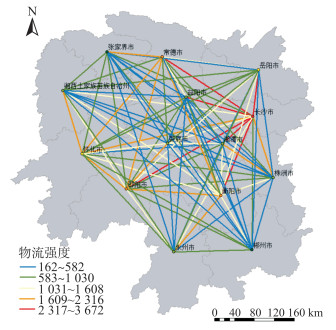 |
| 图 2 城市间平均物流联系强度 Fig.2 Average Intensity Values of Freight Connections Between Cities |
3 基于经典空间交互模型的城市间物流联系强度预测 3.1 重力模型
重力模型公式如下:
| $ T_{i j}=k \frac{P_i P_j}{d_{i j}{ }^\beta} $ | (1) |
式中,Tij表示空间单元i到空间单元j的人流量;k是一个预定义的比例系数;Pi和Pj分别表示i和j的属性信息,一般表示空间单元i和j的人口数量;dij为两个空间单元i和j之间的距离;幂指数β是距离衰减因子,决定了dij对i和j之间相互作用力影响。在本文,Tij表示从城市i到城市j的货运联系强度。
3.2 辐射模型辐射模型[9]参考了物质运动和扩散的规律,是一类无参数模型,其公式为:
| $ T_{i j}=T_i \frac{m_i m_j}{\left(m_i+m_j\right)\left(m_i+m_j+S_{i j}\right)} $ | (2) |
式中,Ti表示空间单元i输出的出行量;mi和mj分别表示i和j的人口数;Sij表示以空间单元i为圆心,以i到j的距离为半径作圆,圆内所有空间单元的人口数之和。在本文,Ti表示从城市i出发的货运量。
3.3 预测效果评价 3.3.1 基于人口数据和重力模型的城市间货运联系强度预测在利用重力模型预测城市间货运联系强度前,首先要确定模型中的距离衰减因子β。本文利用迭代的方法来确定重力模型中β的最优值。首先设定β=[0:0.01:2],即β从0开始,每隔0.01步长取一次值,直到β=2。然后将上述β值代入式(1),Pi和Pj分别用城市i和j的人口数量来表示。最终得到每一个β值下的城市i和j之间的货运联系强度预测值Tij。接着计算每对城市i和j之间货运联系强度的预测值与真实值间的Pearson相关系数。当β=0.79时,Pearson相关系数达到峰值0.83,表明此时重力模型得到的预测值与真实值之间存在很强相关性。
β最优值小于1,说明城市间的距离对两地间的货物流动联系强度影响较小。即城市人口数不变时,若城市间的距离改变,它们之间的货运联系强度也不会发生非常明显的变化。货物流动距离的这一特征与人群移动存在明显差异。在城市间人群移动的相关研究中,β取值通常较高。例如,Liu等[21]利用社交媒体签到数据对中国370个城市中50万人的行动轨迹进行分析,发现人群在不同城市间移动时的距离衰减因子β在1.0~2.0间。Masucci等[22]针对英格兰和威尔士人群通勤流量的研究发现,当β为1.03时重力模型预测效果最好。存在差异的原因主要是货运物流的起讫点很少受到主观因素的影响,弹性较小。货物的长距离移动能力要比人口的长距离移动能力更强,因此对距离的敏感度更小。
将最佳系数β=0.79代入重力模型,以该模型计算得到的货运联系强度预测值与真实值作散点图,如图 3所示,预测值与真实值间的Pearson相关系数为0.84,表明重力模型可以较好地估计城市间物流运输的空间交互。图 3中的大部分散点位于y = x趋势线上方,反映出基于人口数据的预测模型在一定程度上会高估两地之间的货运联系强度。
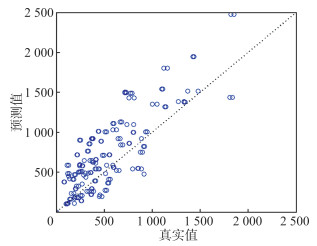 |
| 图 3 货运联系强度真实值与基于人口数据计算的预测值 Fig.3 Real Values of Freight Connection and Their Predicted Values Calculated by Population Data |
3.3.2 基于GDP数据和重力模型的城市间货运联系强度预测
利用GDP数据预测城市间货运联系强度时,重力模型中Pi和Pj分别表示城市i和j的GDP总量。通过迭代方法找到最佳距离衰减因子β为0.73,说明对于不同GDP的城市,城市间距离对两地间货运流量影响较小。城市GDP带给各城市的货运吸引力对空间距离的敏感性不高。其值与基于人口数据来预测货运联系强度时的距离衰减因子值(0.79)差别较小,表明在用GDP数据预测城市货运联系强度时,城市间的距离对两地之间货运联系强度的影响与基于人口数据的预测模型相似。
将β=0.73代入基于GDP数据的城市间货运联系强度预测模型,将由该模型计算的预测值与真实值作散点图,见图 4。预测值与真实值间的Pearson相关系数为0.74。预测效果相对于基于人口数据的预测模型较差。从散点图的分布上看,当真实货运联系强度小于1 000时,大部分散点位于y = x趋势线下方;当真实货运联系强度大于1 000时,大部分散点位于y = x趋势线上方。这表明基于GDP数据的预测模型会高估货运联系较强的城市间的货运联系强度,低估货运联系较弱的城市间的货运联系强度。这主要是因为城市间的GDP差异较人口总量的差异大得多,当用GDP值预测城市间的货运联系强度时,位于研究区外围的城市如郴州、湘西土家族自治州等的GDP很小,但与其他城市的距离又相对较远,因此这些城市间的货运联系强度就很容易被低估。GDP值高的城市如长沙、衡阳、常德等,由于其值比其他城市高很多,根据这些城市的GDP值来预测城市间货运联系强度时则很容易高估。
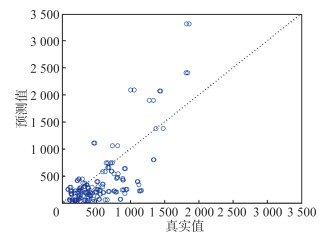 |
| 图 4 货运联系强度真实值与基于GDP数据计算的预测值 Fig.4 Real Values of Freight Connection and Their Predicted Values Calculated by GDP data |
3.3.3 基于辐射模型的预测
根据重力模型的结论,人口数据对两地之间的货运联系强度的预测性更好,因此在辐射模型中也同样采用人口数据对城市间货运联系强度进行预测。将辐射模型得到的货运联系强度预测值与真实值作散点图,如图 5所示。预测值与真实值之间的Pearson相关系数为0.78。从散点图的分布上看,大部分数据点位于y = x趋势线的下方,这说明当城市间真实物流联系强度较大时(大于1 000),辐射模型会在一定程度上低估城市之间的货运联系强度。
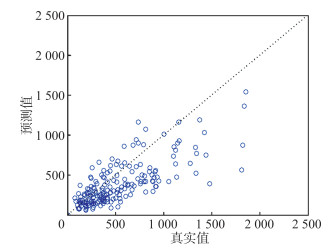 |
| 图 5 货运联系强度真实值与基于辐射模型计算的预测值 Fig.5 Real Values of Freight Connection and Their Predicted Values Obtained by Radiation Model |
4 结束语
本文以湖南省为例,利用大规模货运轨迹数据对城市间货运物流的位移特征和空间交互进行了分析。得到如下结论:①城市间货运物流的位移距离呈双峰威布尔分布,在20 km和200 km左右处出现货运距离的高峰值;②城市间的物流联系强度在累积概率上呈现明显的指数分布,且不同城市间的货运联系强度存在明显差异。少数城市对,如长沙-衡阳、长沙-常德等的货运联系强度在湖南省整个物流网络中明显占主导地位;③在对湖南省各城市间的货运联系强度进行预测时,重力模型的预测结果与真实值间的拟合度较辐射模型高。重力模型会在一定程度上高估两地之间的货运联系强度,而辐射模型则会在一定程度上低估两地之间的货运联系强度。
本文研究表明,在城市间真实货运联系数据难以获取的情况下,可以借助易获取的静态统计数据(如人口数据),利用重力模型、辐射模型对城市间的货运联系强度、物流空间联系强度进行预测。此外,本研究也有助于更好地理解城市间的物流和经济联系,为跨城市的物流设施布局和道路建设提供数据支撑。
目前本研究还存在一定的局限性,如以湖南省的货运物流数据为例的结论在其他省份或者更大的空间尺度上是否仍然适用还有待进一步研究。
| [1] |
Zhao P X, Liu X T, Shi W Z, et al. An Empirical Study on the Intra-Urban Goods Movement Patterns Using Logistics Big Data[J]. International Journal of Geographical Information Science, 2020, 34(6): 1089-1116. DOI:10.1080/13658816.2018.1520236 |
| [2] |
李江涛. 基于货运卡车轨迹大数据的货运OD信息提取方法研究[D]. 北京: 北京交通大学, 2019
|
| [3] |
Yan X Y, Wang W X, Gao Z Y, et al. Universal Model of Individual and Population Mobility on Diverse Spatial Scales[J]. Nature Communications, 2017, 8: 1639. DOI:10.1038/s41467-017-01892-8 |
| [4] |
Gallotti R, Bazzani A, Rambaldi S, et al. A Stochastic Model of Randomly Accelerated Walkers for Human Mobility[J]. Nature Communications, 2016, 7: 12600. DOI:10.1038/ncomms12600 |
| [5] |
Ren Y H, Ercsey-Ravasz M, Wang P, et al. Predicting Commuter Flows in Spatial Networks Using a Radiation Model Based on Temporal Ranges[J]. Nature Communications, 2014, 5: 5347. DOI:10.1038/ncomms6347 |
| [6] |
Song C M, Koren T, Wang P, et al. Modelling the Scaling Properties of Human Mobility[J]. Nature Physics, 2010, 6(10): 818-823. DOI:10.1038/nphys1760 |
| [7] |
González M C, Hidalgo C A, Barabási A L. Understanding Individual Human Mobility Patterns[J]. Nature, 2008, 453(7196): 779-782. DOI:10.1038/nature06958 |
| [8] |
Brockmann D, Hufnagel L, Geisel T. The Scaling Laws of Human Travel[J]. Nature, 2006, 439(7 075): 462-465. |
| [9] |
Simini F, González M C, Maritan A, et al. A Universal Model for Mobility and Migration Patterns[J]. Nature, 2012, 484(7392): 96-100. DOI:10.1038/nature10856 |
| [10] |
Palchykov V, Mitrović M, Jo H H, et al. Inferring Human Mobility Using Communication Patterns[J]. Scientific Reports, 2014, 4: 6174. |
| [11] |
Belyi A, Bojic I, Sobolevsky S, et al. Global Multi-Layer Network of Human Mobility[J]. International Journal of Geographical Information Science: IJGIS, 2017, 31(7): 1381-1402. DOI:10.1080/13658816.2017.1301455 |
| [12] |
Kang C G, Liu Y, Guo D S, et al. A Generalized Radiation Model for Human Mobility: Spatial Scale, Searching Direction and Trip Constraint[J]. PLoS One, 2015, 10(11): e0143500. DOI:10.1371/journal.pone.0143500 |
| [13] |
Okoko E. The Spatial Pattern of Urban Goods Movement in Akure, Nigeria[J]. Pakistan Journal of Social Sciences, 2008, 5(3): 226-234. |
| [14] |
Ogunsanya A A. Spatial Pattern of Urban Freight Transport in Lagos Metropolis[J]. Transportation Research(Part A): General, 1982, 16(4): 289-300. DOI:10.1016/0191-2607(82)90056-5 |
| [15] |
Ogden K W. The Distribution of Truck Trips and Com modity Flow in Urban Areas: A Gravity Model Analysis[J]. Transportation Research, 1978, 12(2): 131-137. DOI:10.1016/0041-1647(78)90052-7 |
| [16] |
边馥苓, 杜江毅, 孟小亮. 时空大数据处理的需求、应用与挑战[J]. 测绘地理信息, 2016, 41(6): 1-4. |
| [17] |
Comendador J, López-Lambas M E, Monzón A. A GPS Analysis for Urban Freight Distribution[J]. Procedia-Social and Behavioral Sciences, 2012, 39: 521-533. DOI:10.1016/j.sbspro.2012.03.127 |
| [18] |
Fu Y H, Shi X F. Research on Freight Truck Operation Characteristics Based on GPS Data[J]. Procedia - Social and Behavioral Sciences, 2013, 96: 2320-2331. DOI:10.1016/j.sbspro.2013.08.261 |
| [19] |
肖作鹏, 邹海翔, 孙永海. 利用货车GPS数据推演城市内部物流联系: 以深圳市为例[J]. 西部人居环境学刊, 2017, 32(1): 9-15. |
| [20] |
湖南省统计局, 国家统计局湖南调查总局. 湖南统计年鉴2019[M]. 北京: 中国统计出版社, 2020.
|
| [21] |
Liu Y, Sui Z W, Kang C G, et al. Uncovering Patterns of Inter-Urban Trip and Spatial Interaction from Social Media Check-in Data[J]. PLoS One, 2014, 9(1): e86026. DOI:10.1371/journal.pone.0086026 |
| [22] |
Masucci A P, Serras J, Johansson A, et al. Gravity Versus Radiation Models: On the Importance of Scale and Heterogeneity in Commuting Flows[J]. Physical Review E, 2013, 88(2): 022812. DOI:10.1103/PhysRevE.88.022812 |
 2022, Vol. 47
2022, Vol. 47


