| 高景一号卫星影像DSM自动提取方法 |
2016年12月28日,高景一号(SuperView-1)01和02星于太原卫星发射场顺利升空,两年后03和04星也相继进入轨道,四星组网后,可实现全球任一点的1天重访,标志着中国完全自主的遥感卫星商业化运营服务迈出了第一步[1],高景一号首次将中国遥感卫星分辨率提高到了0.5 m。
高景一号为高分辨率、高精度数字表面模型(digital surface model, DSM)的自动提取提供了重要数据来源。DSM的自动提取依赖有效、可靠的立体匹配算法,已有的立体匹配算法有局部匹配算法、全局匹配算法和半全局匹配算法[2]。全局匹配算法由于需要求解全局最优解,具有极高的计算复杂度,难以在遥感影像中得到广泛应用。局部匹配算法一般缺少有效的匹配约束条件,在弱纹理区域会产生较多的错误匹配,可靠度不高。Hirschmuller[3]提出的半全局匹配(semi-global matching, SGM)算法利用惩罚系数实现分片平滑约束,通过至少8个方向的代价积聚实现全局能量最小化。大量试验表明,SGM算法兼具较好的匹配效果和较高的执行效率,已经在航空、航天遥感影像处理中得到应用[4, 5]。在实际应用中,SGM算法需要较大的内存存储匹配代价立方体和积聚代价立方体,内存容量取决于影像的尺寸和视差搜索范围。因此,不能直接将SGM算法应用到大尺寸卫星图像上。
本文以高景一号立体像对为研究对象,首先研究了核线影像生成;然后采取对核线影像分块SGM匹配再融合的策略,以减少SGM的内存消耗和提高匹配效率;最终实现DSM的高精度提取。
1 DSM提取 1.1 DSM提取流程从卫星影像中提取DSM的流程包括空三平差、核线影像生成、密集匹配和DSM生成[6-8]等4个步骤。空三平差的目的是对影像进行空间定向,减少定位误差,它作为本文方法的预处理流程。本文主要研究流程中核线影像生成和改进的半全局密集匹配这两个核心环节。所有输入影像都经过空三平差处理,带有高精度有理多项式系数(rational polynomial coefficients, RPC)文件。
1.2 核线生成方法核线影像就是同名像点位于同一影像行的影像,即消除了上下视差的立体匹配片。利用核线影像能将二维匹配搜索问题转化为一维搜索问题,从而大大提高匹配的效率和正确率[9]。在线阵卫星影像中,核线关系如图 1所示,P为物方点,p和q为其投影在像方的同名像点,hmax和hmin为测区最大和最小高程,过q点的右核线如虚线所示。核线具有以下两个特性:①近似平直性,线阵影像核线是类似双曲线的曲线,在小范围内可近似看作直线。②局部共轭性,同名核线对仅在局部范围内存在。
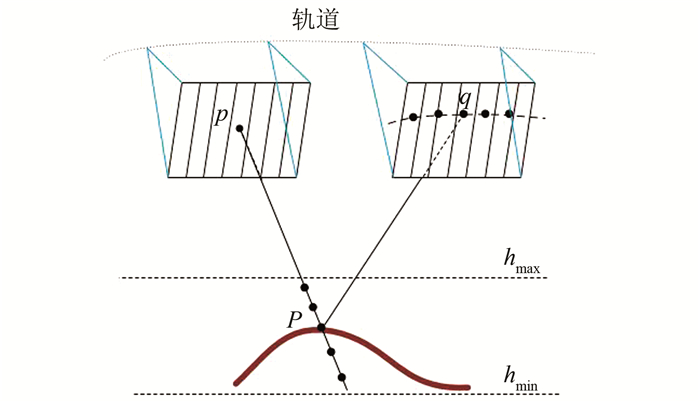 |
| 图 1 线阵卫星核线几何 Fig.1 Epipolar Geometry in Linear Array Scanners |
目前,主流的核线纠正方法可以分为基于像方[10]和基于物方[11]两类。基于像方不仅能够获得接近于零级别的上下视差,并且能保持左右视差与高程的线性比例关系,因而被广泛采用。该方法的算法流程如下。
1) 采用投影轨迹法以一定高程间距获取均匀覆盖全图的投影轨迹点,左右像片投影轨迹点存在一一对应关系,同一投影起点生成的轨迹点构成一条核曲线;
2) 对左右影像分别旋转一个角度,使得核曲线大致平行于水平方向,此时所有轨迹点沿水平方向依次排列,在竖直方向存在微小错位;
3) 调整轨迹点坐标,令同一轨迹线上的轨迹点y坐标值相同,x坐标值不变,以此来消除上下视差;
4) 重排前后的轨迹点分布如图 2所示,采用多项式模型建立重排前后坐标转换关系,二阶多项式模型为:
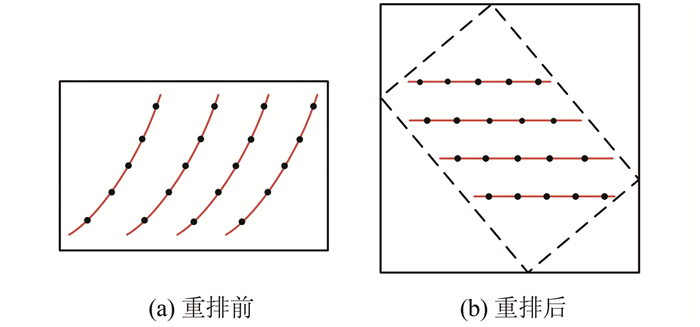 |
| 图 2 核线轨迹点重排前后 Fig.2 Before and After the Relocation of the Epipolar Curve Points |
| $\left\{ {\begin{array}{*{20}{l}} {{x^\prime } = {a_1} + {a_2}x + {a_3}y + {a_4}{x^2} + {a_5}xy + {a_6}{y^2}}\\ {{y^\prime } = {b_1} + {b_2}x + {b_3}y + {b_4}{x^2} + {b_5}xy + {b_6}{y^2}} \end{array}} \right. $ | (1) |
式中,x和y为重排前原始影像坐标; x′和y′为重排后核线影像坐标; (a1, a2, a3, a4, a5, a6)和(b1, b2, b3, b4, b5, b6)分别为多项式模型系数,由轨迹点拟合可以得到。
利用式(1)可实现原始影像到核线影像的坐标转换,从而可实现左右核线影像的重采样。
1.3 改进的半全局密集匹配SGM算法包括匹配代价计算、代价积聚、视差计算和视差图优化4个步骤。
匹配代价是衡量两个像素相似性程度的度量指标。归一化相关系数(normalized cross correlation, NCC)、绝对差值和(sum of absolute differences, SAD)、互信息(mutual information, MI)和Census是几种常见的匹配代价,选择正确有效的匹配代价对SGM的成功至关重要。Census由于对参数化不敏感,能够提供较为鲁棒的结果,且计算速度快,因而适合于大部分卫星影像数据,本文采用9像素×9像素窗口计算Census代价。在代价计算时,需指定视差范围,对于左核线影像每一个像素,会对应生成一个匹配代价向量。整幅图像的代价计算过程如图 3所示,m和n分别是影像长和宽,S代表视差范围。生成的匹配代价立方体长宽与近左核线影像长宽相同,高度等于视差范围。
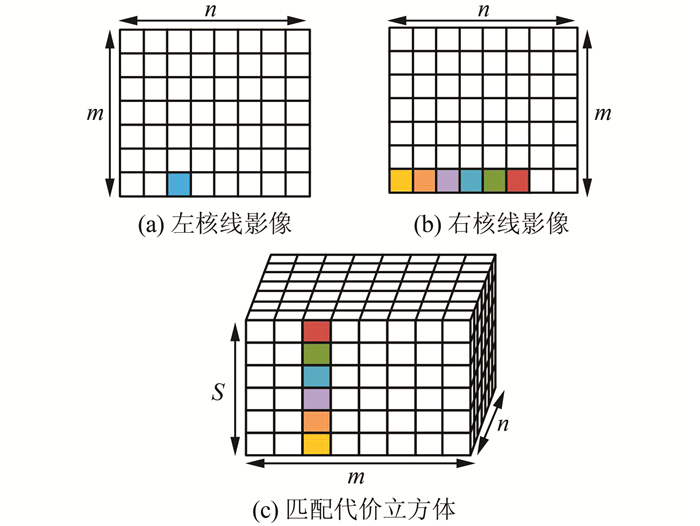 |
| 图 3 匹配代价计算和代价立方体 Fig.3 Matching Cost Calculation and Costs Cube |
SGM的代价积聚采用动态规划的方法,合并至少8个方向的一维动态规划结果实现二维的代价积聚。式(2)显示了单条路径上的代价聚合函数;式(3)显示了所有路径上的代价积聚累加和。
| $\begin{array}{*{20}{l}} {{L_r}(p,d) = C(p,d) + }\\ {\quad \min \left( {\begin{array}{*{20}{l}} {{L_r}(p - r,d),{L_r}(p - r,d - 1) + {P_1}}\\ {{L_r}(p - r,d + 1) + {P_1},\mathop {\min }\limits_i {L_r}(p - r,i) + {P_2}} \end{array}} \right) - }\\ {\mathop {\min }\limits_k {L_r}(p - r,k)} \end{array} $ | (2) |
式中,p为像素位置;d为视差值;C(p, d)为匹配代价;Lr(p, d)为路径r上在视差d处的代价积聚值;P1和P2分别为对视差变化等于1和大于1的惩罚系数;P1 < P2;式中最后减去
| $S(p,d) = \sum\limits_{r = 1}^8 {{L_r}} (p,d) $ | (3) |
式中,S(p, d)称为聚合代价立方体。对于每一个像素,从式(3)选择聚合代价最小的视差作为最优视差,从而生成最终的视差图D:
| $D = {\min _d}S(p,d) $ | (4) |
为了获得更加精细平滑的视差图,需要对视差图进行亚像素级内插处理。常用的有二次函数内插,该方法利用二次曲线拟合相邻匹配代价,并给出最小代价处的视差值作为插值结果。SGM需要临时开辟的内存有匹配代价立方体C(p, d)、聚合代价立方体S(p, d),以及视差图D。临时内存的大小取决于影像的尺寸和视差范围,而卫星影像尺寸普遍较大,这样的数据将消耗大量的内存。本文解决的方法是采用分块匹配策略(图 4),首先将核线影像分割成大约4 000像素×4 000像素的小图,然后分别计算每个小图的视差,最后将每个小图的结果融合成一个完整的视差图。为了保证分块之间的平滑过渡,块与块之间保证10%左右的重叠度,重叠区域的视差采用加权平均的方式进行融合。
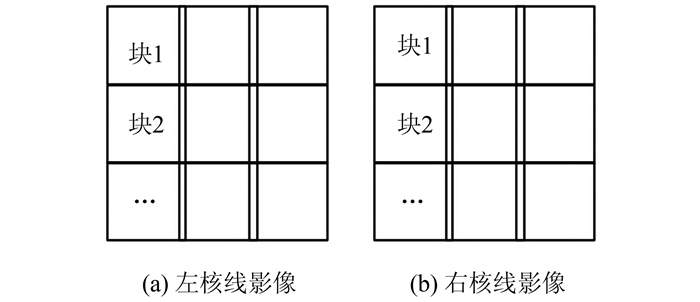 |
| 图 4 核线影像分块匹配 Fig.4 Deviding Epipolar Images into Small Image Tile |
2 核线试验结果分析
试验数据采用高景一号02星拍摄的印度某地区双视立体像对,获取时间为2017-06-14,测区位于27.24°N、75.85°E。影像分辨率为0.5 m,卫星拍摄侧摆角为21.44°,测区平均高程约680.4 m,基高比为0.704,影像大小为24 905像素×25 834像素。该区域为山区盆地地形,中间为平地,周围有突起的山体。影像的相对位置如图 5所示。
 |
| 图 5 原始影像分布 Fig.5 Distribution of Original Images |
2.1 核线曲率分析
生成核线影像之前需要对高景一号核线特性进行分析,以检查核线曲率大小,从而为今后该传感器核线纠正方法的选择提供参考依据。在左影像上选择某一像点作为投影起点,根据投影轨迹法,不断改变投影高程面可得到一系列投影轨迹点。用一条直线拟合该系列轨迹点,拟合残差用来评价该核曲线的曲率大小。在影像范围内选择3个均匀分布的投影起点,可得到3条均匀分布的核曲线。核曲线分布如图 6所示,直线拟合残差如表 1所示。
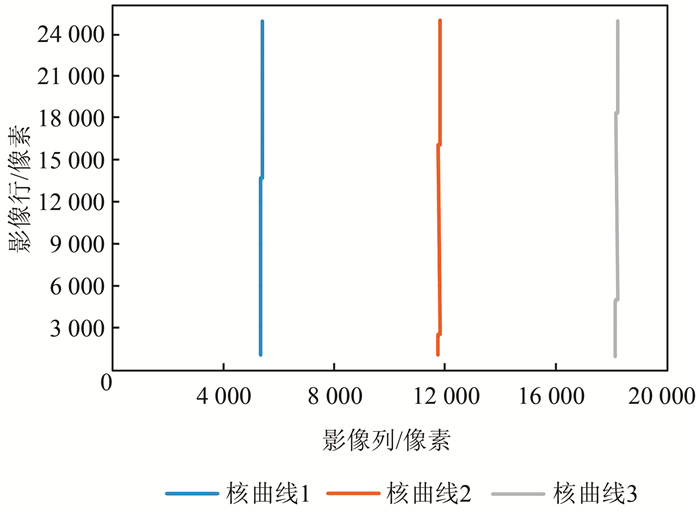 |
| 图 6 核线拟合分析 Fig.6 Epipolar Curve Fitting Analysis |
| 表 1 核曲线拟合残差 Tab.1 Epipolar Curve Fitting Residuals |
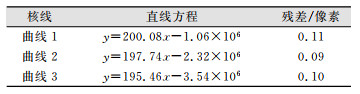 |
可以看到,3条核曲线拟合残差都在0.1个像素左右,说明核曲线具有较低的曲率。如图 6所示,核线之间互相平行,表现出较好的平行性。因此可以得出结论,高景一号立体像对核线关系较为稳定,核线具有平直特性,利用常规核线纠正方法能较好地消除上下视差。
采用基于像方方法生成的核线影像如图 7(a)所示,通过人工刺点在核线影像上选择了62个同名像点,上下视差分布如图 7(b)所示,最大上下视差0.64个像素,低于1个像素,满足密集匹配输入要求。
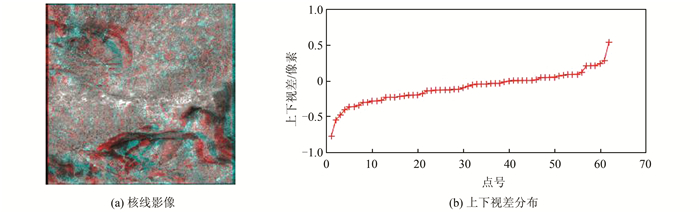 |
| 图 7 核线影像和上下视差检查 Fig.7 Epipolar Image and Y-Parallax Check |
2.2 DSM提取结果分析
试验核线影像共被分成36个小块单独进行密集匹配,所有生成的小块视差图被融合生成一张完整的视差图。利用RPC进行交会获取每个像素的物方坐标,从而生成测区物方三维点云,最后通过点云栅格化生成1 m分辨率的DSM产品。
DSM整体视图如图 8所示,可以看出,本文方法生成的DSM完整准确的表达了成像地区宏观地形。重建的局部细节如图 9所示。图 9(a)、图 9(c)为重建的地形;图 9(b)、图 9(d)为对应的正射图;图 9(e)为三维透视效果图。山体的走向和纹理细节表现丰富,尤其是平原中突起的山丘被准确重建,平原地形平整,无明显误匹配。
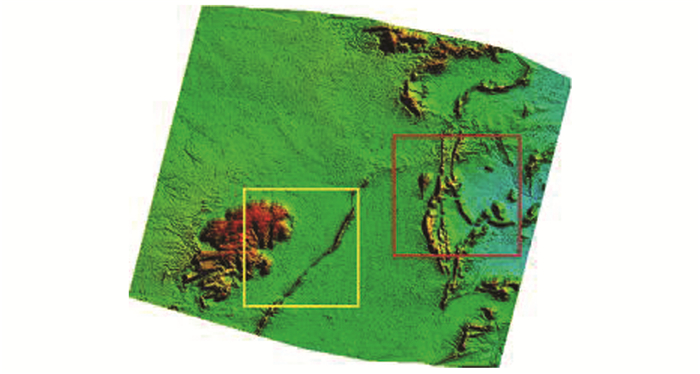 |
| 图 8 高景一号1 m DSM Fig.8 SuperView-1 DSM at 1 m DSM |
 |
| 图 9 DSM细节显示 Fig.9 DSM Detail Display |
由于缺少测区实地勘测地形参考数据,本文无法对生成的DSM进行绝对精度的评价。本文将空三特征点作为检查点,用来评价DSM相对精度,从而验证本文方法可靠性。选择40个空三特征点作为理想精确参考点,通过前方交会重建出参考点物方坐标,与生成的DSM相应点做差值,差值结果为:最大误差为2.21 m,平均误差为1.37 m,中误差为1.43 m,优于1.5 m,表明本文方法具有一定的可靠性。
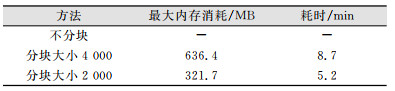
为了验证本文分块匹配的有效性,表 2列出了SGM改进前后的内存消耗和时间效率对比,试验所用计算机配置为Intel(R) Core(TM) i5-3230MB CPU @2.60 GHz,内存6 GB。由于核线影像大小达到25 000像素×25 000像素,不分块匹配的情况下,内存分配不足,SGM运行失败。分块以后能正确生成DSM,并且分块大小对运行效率有一定影响,可以看到,分块大小为2 000像素左右时,运行耗时和内存消耗都得到减少。
| 表 2 算法内存消耗和时间效率 Tab.2 Algorithm Memory Consumption and Time Efficiency |
 |
3 结束语
本文针对超高分辨率国产高景一号卫星立体数据,提出了一种高分辨率DSM自动提取方法,分析了立体像对核线特性。实验表明,该传感器核线具有平直特性,且核线关系较为稳定,生成的核线影像上下视差优于一个像素。本文改进了SGM算法,采用影像分块匹配再融合的策略,减少了SGM算法内存消耗,提高了运行效率。试验结果表明,该方法生成的高分辨率DSM宏观地形完整,山地地形重建准确且纹理细节表现丰富,平原地区无明显误匹配。本文方法在高景一号上的应用取得了较好的效果。本文的不足在于未能给出高景一号DSM产品的绝对高程精度,有待下一步继续拓展研究。
| [1] |
郭晗. 高景一号正式商用, 中国商业遥感进入0.5 m时代[J]. 卫星应用, 2017(5): 62-63. DOI:10.3969/j.issn.1674-9030.2017.05.013 |
| [2] |
Scharstein D, Szeliski R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms[J]. International Journal of Computer Vision, 2002, 47(1-3): 7-42. |
| [3] |
Hirschmuller H.Accurate and Efficient Stereo Processing by Semi-Global Matching and Mutual Information[C].IEEE Computer Society Conference on, San Diego, USA, 2005
|
| [4] |
Haala N.The Landscape of Dense Image Matching Algorithms[C].Photogrammetric Week'13, Berlin, Germany, 2013
|
| [5] |
岳庆兴, 高小明, 唐新明. 基于半全局优化的资源三号卫星影像DSM提取方法[J]. 武汉大学学报·信息科学版, 2016, 41(10): 1279-1285. |
| [6] |
Zhang L.Automatic Digital Surface Model (DSM) Generation from Linear Array Images[D].Zurich: Swiss Federal Institute of Technology Zurich, 2005
|
| [7] |
张云翔, 于杰. 基于资源三号的DSM自动生成方法与质量控制[J]. 测绘地理信息, 2017, 42(4): 43-46. |
| [8] |
张静, 杨博, 王密, 等. 基于资源3号影像的全国DOM快速制作方法[J]. 测绘地理信息, 2016, 41(6): 70-74. |
| [9] |
张永军, 丁亚洲. 基于有理多项式系数的线阵卫星近似核线影像的生成[J]. 武汉大学学报·信息科学版, 2009, 34(9): 1068-1071. |
| [10] |
Oh J, Lee W H, Toth C K, et al. A Piecewise Approach to Epipolar Resampling of Pushbroom Satellite Images Based on RPC[J]. Photogrammetric Engineering & Remote Sensing, 2010, 76(12): 1353-1363. |
| [11] |
胡芬, 王密, 李德仁, 等. 基于投影基准面的线阵推扫式卫星立体像对近似核线影像生成方法[J]. 测绘学报, 2009, 38(5): 428-436. DOI:10.3321/j.issn:1001-1595.2009.05.009 |
 2019, Vol. 44
2019, Vol. 44


