| 一种百度地图坐标高精度解密方法 |
随着移动互联网和移动终端的飞速发展,互联网地图经历了爆发式增长[1]。位置服务已成为信息服务业的新兴业态和重要组成部分[2]。百度地图作为提供位置服务的互联网地图中的一员,已被广泛应用于地理信息管理系统[3-6]和位置服务[7-10]中。
为了解决百度地图在实际应用中坐标偏移的问题,有学者提出了基于人工神经网络的坐标解密方法[11]、格网法[12]、基于邻近点偏移量相近的方法[13]、等量偏移法及其二阶差分法[14]和公式拟合的方法[15]。前几种方法各有局限,如精度不够高、需要提前获取大量格网点形成修正数据库、适用范围窄等,仅等量偏移二阶差分法精度较高、适用性广。
但是,在同样假设的前提下,基于邻近点偏移量相近的方法与等量偏移法的文献结果不一致,这说明实验数据选择有不完善之处,结论有待验证。为检验百度坐标转换接口的安全性以及等量偏移二阶差分法的解密精度,本文提出了等量偏移迭代逼近(equivalent offset iterative approximation,EOIA)法,在中国大陆范围内随机选取坐标点进行实验,并将其与等量偏移二阶差分法进行比较分析。
1 坐标解密方法 1.1 等量偏移法及其二阶差分法对于坐标点PW,通过应用程序接口(application program interface,API)接口转换后可得到BD09坐标系下的对应点PB,对PB进行一次坐标加密,得到点PB1。
等量偏移法假设电子地图经加密算法处理后,为了保持地图上各种地物的相对位置关系,相邻两点的坐标加密偏移量是接近的。其公式如下:
| $ P_W^1=2 P_B-2 P_B^1 $ | (1) |
将点PB1进行一次坐标加密,得到点PB2,由式(1)可以推出二阶的差分公式:
| $ P_W^1=3 P_B-3 P_B^1+P_B^2 $ | (2) |
现假设临近点的坐标偏移量近似相等,且距离越近的点,坐标偏移量越接近。经过偏移改正的PW1>比PB更接近点PW,将PW1作为PW的临近点,使用等量偏移法处理后可以获得PW的估值点PW2。距离越近的点,坐标偏移量越接近,那么由更近的临近点通过等量偏移法计算出的坐标估值更接近原始值,即PW2比PW1更接近PW。若假设一直成立,迭代使用前一次等量偏移法计算的估值作为本次等量偏移的临近点,则第i + 1次等量偏移法计算的估值PWi为:
| $ P_W^{i+1}=\operatorname{API}\left(P_W\right)-\operatorname{API}\left(P_W^i\right)+P_W^i $ | (3) |
式中,API(·)表示地图坐标在线转换接口函数。当PWi+1 = PWi时,有API(PW)= API(PWi),即PW = PWi。
当假设一直成立时,可以通过迭代使用等量偏移的方法来逼近PW,由此形成了EOIA法,式(3)即为EOIA法的计算公式。
2 实验分析 2.1 数据选取与实验设计在中国大陆范围内随机选取1 000个坐标点作为原始坐标的参考值,用百度地图坐标转换接口处理这些坐标点,获得对应的待解密坐标点。实验方案步骤如下:①用等量偏移二阶差分法(方法1)和EOIA法(方法2)分别处理这些待解密点,计算对应的坐标估值;②对比坐标估值与参考值,并将点位分带投影到通用横轴墨卡托坐标系中,计算点位误差;③将1 000组数据随机分成500个点对,计算两点间的大地距离,分布情况见图 1,并统计大地距离相对误差;④逐次计算方法2每一次迭代后的点位误差,分析方法2的效率。
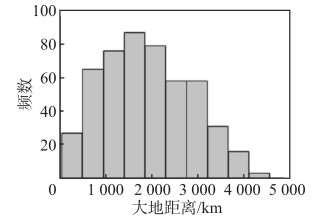 |
| 图 1 大地距离分布 Fig.1 Distribution of Geodetic Distances |
2.2 结果与分析 2.2.1 点位误差
两种方法的点位误差见图 2。观察图 2(a)中的经纬度误差可知,方法1的点位误差有一定线性规律,结合东、北方向误差图中多出的3条线性趋势可知,方法1的解密精度会随研究区域改变。该结论与文献[14]的结果有所不同。此处选取的数据范围更大,因此结果的可信度更高。由图 2(b)可知,方法2的点位误差在矩形区域内呈随机噪声特性,所以方法2稳健性较好,其解密精度不会随研究区域改变,且达到了厘米级,这说明百度地图坐标转换接口有一定保密风险。
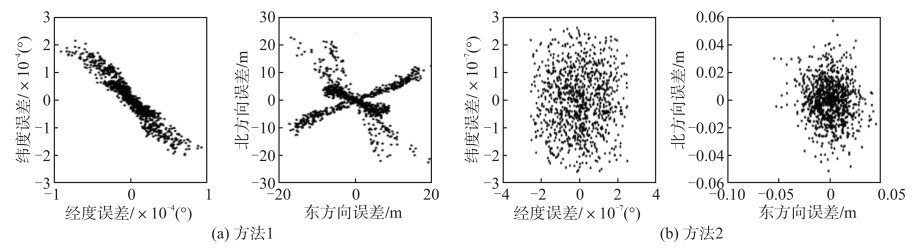 |
| 图 2 点位误差 Fig.2 Point Errors |
2.2.2 大地距离相对误差
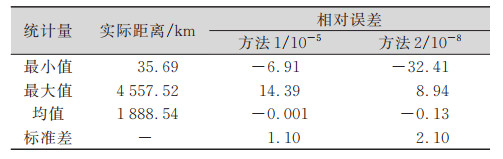
两种方法的大地距离解密误差见图 3。方法1、方法2的大地距离误差分别在40 m、0.04 m以内。点对的大地距离相对误差见表 1,坐标点对的实际大地距离覆盖了短、中、长基线和超长基线,方法1和方法2的相对误差分别在10-4和10-7量级。方法1的距离相对误差与文献[14]的保持一致,而方法2的距离相对误差更小,且呈现出稳定趋势。
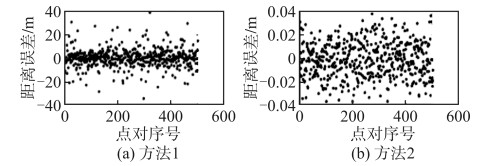 |
| 图 3 大地距离误差 Fig.3 Geodetic Distance Errors |
| 表 1 大地距离相对误差 Tab.1 Relative Errors of Geodetic Distance |
 |
2.2.3 方法效率
方法2逐次迭代后的点位误差见图 4。方法1需要进行二阶差分,所以使用了两次在线坐标转换请求,方法2每次迭代都要使用1次在线坐标转换,迭代1次时,方法2退化为等量偏移法。图 4表明,方法2迭代1次时,东方向、北方向的点位误差分别在32 m和50 m以内,具有两条明显的线性趋势,与文献[14]结果不同,且精度较低;迭代2次后,东方向和北方向的点位误差分别在0.25 m、0.35 m以内;迭代3次后,东方向和北方向的点位误差均在0.06 m以内,对比第4次迭代,点位误差已趋近收敛。实验结果表明,在两次在线坐标转换请求次数下,方法2的解密结果明显比方法1的好,点位误差已低至分米级;再增加一次坐标转换,点位误差可降到厘米级,而且这个结果已经趋近最终的迭代结果。虽然方法2是迭代逼近计算,但在效率上不输方法1,且精度更高,实际迭代次数表明绝大部分点位只需要3次迭代就能获得高精度的坐标解密结果。
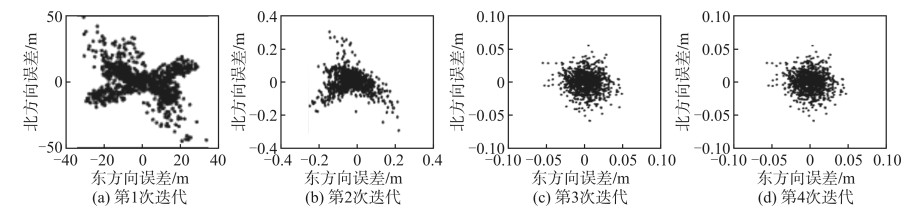 |
| 图 4 逐次迭代点位误差 Fig.4 Point Errors of Successive Iteration |
3 结束语
本文选用中国大陆范围内的随机数据,从点位误差、距离误差、效率3个方面,对比分析了等量偏移二阶差分法和EOIA法的坐标解密结果。结果表明,等量偏移法和等量偏移二阶差分法的误差水平分别在50 m、23 m以内,且误差分量具有明显的线性趋势;EOIA法的误差在0.06 m以内,方法具有很强的稳健性。EOIA法在百度地图坐标解密中能获得厘米级的点位误差和10-7量级的距离相对误差,且该方法适用范围广、效率高、易操作。由于该方法需要调用百度地图坐标转换接口,所以百度地图坐标转换接口是存在保密风险的,为保护相关隐私,建议对接口函数的输入参数和输出值进行截位处理。
| [1] |
杨洪泉. 大众电子地图的应用现状及发展趋势[J]. 测绘通报, 2014(11): 37-41. |
| [2] |
刘经南, 郭文飞, 郭迟, 等. 智能时代泛在测绘的再思考[J]. 测绘学报, 2020, 49(4): 403-414. |
| [3] |
李乐林, 宋炜杰, 郭程方. 基于Android手机的移动测量软件设计与开发[J]. 测绘地理信息, 2015, 40(4): 35-37. |
| [4] |
姚周祥, 花向红, 王东阁, 等. 基于Android平台的点之记管理系统的实现[J]. 测绘地理信息, 2017, 42(2): 5-7. |
| [5] |
陈昌鸣, 向煜. 基于移动GIS的低压营配贯通采集系统的设计与实现[J]. 测绘地理信息, 2018, 43(5): 113-115. |
| [6] |
唐兆鹏, 花向红, 张伟, 等. GNSS高程拟合信息和点位环境可视化系统[J]. 测绘地理信息, 2020, 45(2): 56-59. |
| [7] |
刘佳, 季民, 张春生, 等. 土地常态化移动巡查系统的构建[J]. 测绘地理信息, 2019, 44(6): 23-26. |
| [8] |
王刚, 李志斌, 李洋. 电网工程移动环评水保信息系统的设计与实现[J]. 测绘地理信息, 2018, 43(5): 100-103. |
| [9] |
柳开弘, 王学文. 基于Android平台的GPS面积测量软件开发[J]. 科技创新导报, 2017, 14(11): 161-164. |
| [10] |
朱峰, 赵婷婷. 基于百度地图API的网点成图平台的开发与应用[J]. 测绘地理信息, 2019, 44(1): 121-123. |
| [11] |
潘伟洲, 陈振洲, 李兴民. 基于人工神经网络的百度地图坐标解密方法[J]. 计算机工程与应用, 2014, 50(17): 110-113. |
| [12] |
潘盛辉, 张硕望. 移动终端百度地图偏移修正方法的研究[J]. 信息通信, 2014, 27(10): 40-41. |
| [13] |
陈大业, 刘佳, 卢凤晖, 等. 基于Web的坐标数据解析方法[J]. 邮电设计技术, 2015(5): 43-47. |
| [14] |
杨丁亮, 刘志平, 仲崇武. 百度地图坐标解密方法精度分析[J]. 测绘通报, 2018(7): 43-47. |
| [15] |
常梦阳, 刘志强. 互联网地图间坐标转换方法研究[J]. 现代测绘, 2018, 41(1): 19-22. |
 2022, Vol. 47
2022, Vol. 47


