| 基于边界搜索的海量水深数据抽稀方法 |
2. 天津海事测绘中心, 天津, 300222
2. Tianjin Hydrographic Center, Tianjin 300022, China
随着现代海洋测绘技术的发展, 多波束水深测量系统目前已经被广泛应用到现代海底地形测量的工作中。与传统的单波束测深系统每次测量只能获得测量船垂直下方一个海底测量深度值相比, 多波束探测能获得一个条带覆盖区域内多个测量点的海底深度值, 具有测量范围大、测量速度快、精度和效率高等优点, 适合进行大面积的海底地形探测[1]。海量化的水深数据能够更加详细地描述海洋地形, 保障航海安全[2]。
庞大的水深数据虽然极大地促进了海洋信息化的研究, 但是TB级的水深数据存在大量的数据冗余, 为数据的存储组织管理和深层次处理及应用带来巨大的负担, 不利于数据成果编制以及海图生产。高效地压缩海量多波束水深数据能够更好地利用水深数据, 提高水深处理工作效率, 节约系统硬件资源, 利于快速成图, 能够创造出客观的经济效益[3]。如何在保障航海安全性和海底地形完善性的前提下, 对多时相的海量水深数据进行抽稀压缩, 成为当前海事信息研究领域的重要课题。
随着计算机技术的发展, 以及地理信息系统研究领域的不断扩大, 许多成熟的研究方法和软件被应用到原始水深数据的处理上。目前较多的多波束水深数据抽稀方法中, 基于网格的逐点抽稀的方法对水深数据进行抽稀, 虽然能够达到一定的抽稀效果, 但是处理速度比较慢, 效率低下[4]。本文针对上述问题展开研究和讨论, 提出基于时间和比例尺对水深数据基于边界搜索进行抽稀处理的方法, 对水深数据进行提取抽稀分层, 有助于水深数据的组织管理, 并将该方法应用到水深数据的实际生产使用中。
1 海量水深数据的边界搜索及抽稀很多方法被应用到海量水深数据的抽稀研究中, 传统方法有基于Douglas-Peucker算法的水深抽稀方法[5], 基于网格的逐点抽稀和基于区域范围的抽稀等。基于Douglas-Peucker算法的水深抽稀方法将水深数据的每ping的水深剖面看作空间曲线, 然后应用Douglas-Peucker算法进行抽稀, 但水深测深数据属于面测量模式, 将测深剖面看作空间曲线不合理[6]。
基于网格的逐点抽稀方法的主要思路是:根据处理范围, 建立空间网格, 确定抽稀阈值, 基于网格采用一定的抽稀规则对离散水深点数据进行抽稀, 抽稀规则为保留网格内时间较新的点, 当时间一致时, 保留水深值较浅的点。基于网格的逐点抽稀方法如图 1所示。
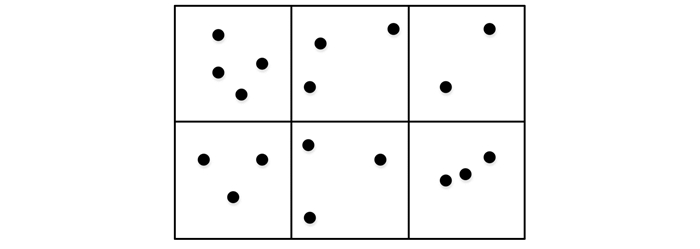 |
| 图 1 基于网格的逐点抽稀 Fig.1 Pointwise Diluting Based on Grid |
基于边界搜索的水深数据抽稀方法, 主要思路是通过提取水深离散点的边界范围, 提高水深点抽稀的效率。根据水深测量工程号生成离散水深点的空间搜索边界, 裁剪重叠区域范围, 提取空间边界范围内的水深数据, 生成原始底层水深数据; 根据不同的比例尺, 不同的抽稀阈值, 以底层水深数据为基础进行数据抽稀, 保留时间较新的点, 在时间相等的情况下, 保留水深值较浅的点, 确保航海安全性。不同的比例尺对应不同的水深数据层, 每层数据的抽稀以原始底层数据为基础, 同时结合上一层水深数据进行抽稀。该抽稀方法的关键在于如何高效提取离散水深点的边界范围, 以及如何对边界范围内的水深数据抽稀处理。
1.1 离散水深点集的区域边界搜索基于边界搜索的水深数据抽稀方法首先需要根据水深工程文件提取水深离散点的边界范围。提取离散点边界的具体思路是:根据离散水深点集的边界特征构建凸壳[7, 8], 然后使用凸壳内缩法搜索离散点集群的边界[9]。
初步构建的凸壳边界范围很大, 需要在凸壳的基础上逐渐细化, 找寻离散点集的最小包围盒, 也即搜索离散点集的边界范围。利用离散点集的凸壳特征, 逐步内缩, 完成离散点集区域边界的检测。内缩规则为:有凸壳点A、B, 判断线段AB是否满足阈值条件(图 2水深点间距0.6 cm, 设定阈值为0.000 025), 即AB的长度是否达到了寻找内点的标准。在线段AB满足阈值的前提下, 对凸壳内点P, AP和AB夹角为θ, 若sinθ>0, cosθ>0, 且P到AB的投影点D在线段AB上, 则定义满足以上3个条件的点P为AB之间的内点。内点的定义是为了满足P是AB之间且在凸壳内部的点。其中sinθ>0保证了P在凸壳内部, cosθ>0和P到AB的投影点D在线段AB上, 保证了点P在线段AB的正上方, 点Q和点S因不符合规则而不考虑凸壳内缩计算。示意如图 2所示。
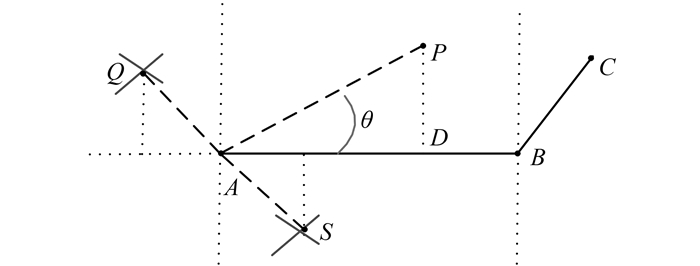 |
| 图 2 内点定义准则 Fig.2 Defined Guidelines of Inside-Points |
通过不断寻找边界之间的内点, 达到压缩凸壳, 搜索边界的目的[10, 11]。寻找离散点边界算法示意如图 3所示。
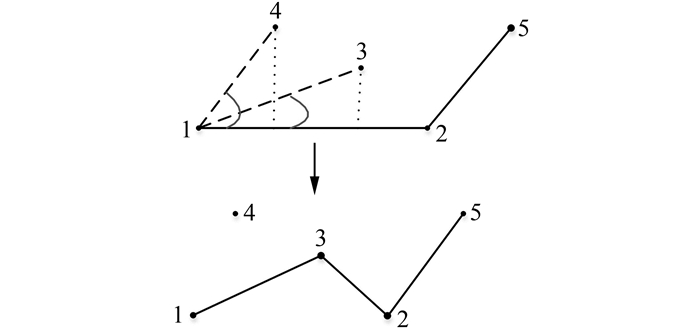 |
| 图 3 边界搜索算法示意图 Fig.3 Diagram of Boundary Searching Algorithm |
算法的具体步骤为:
1) 对凸壳点A、B, 判断线段AB是否满足阈值, 如果满足阈值则进行步骤2);否则跳过该点, 对点B、点C进行步骤1)。
2) 对在AB之间的内点P, AP和AB夹角为θ, 取cosθ最大的内点, 加入边界。
3) 以AC为边界, 对AC, 进行步骤1);如果搜寻完毕后, 对凸壳的下一条边进行步骤1)。
1.2 边界范围内的水深数据抽稀对边界内的水深数据进行抽稀处理, 需要依据一定的抽稀准则:①保留海底地形特征信息, 确保航海保障安全[12]; ②经过抽稀的水深数据应该具有时效性, 某一区域范围内保留下的水深点须是最新采集的水深数据, 但是当采集时间相同时, 保留水深值较小的点(即水深点较浅); ③水深数据严格按照测量时的比例尺信息进行处理[13]。
由于水深测量区域的多重叠性, 在水深数据的抽稀过程中, 容易造成重复区域内数据的重复抽稀, 导致抽稀结果的数据冗余, 因此, 需要对边界区域进行判断, 如果有重叠空间区域, 则不对该区域内的数据进行重复抽稀。具体规则为:
1) 对边界范围A, 如果A与已有边界范围B存在交集, 则求A与B的补集C(其中C=A-B), 依次读取边界范围C内的水深数据D1, D2, …, Dn; 如果A与已有边界范围B不存在交集, 则依次读取边界范围A内的水深数据D1, D2, …, Dn。
2) 以Di为圆心, 阈值T为半径建立缓冲区, 示意如图 4所示。对覆盖范围内的所有点, 抽稀规则为按照测量时间排序, 依次比较各点, 保留测量时间较新的点。若两个点测量时间一样, 如果点Di的水深值大于点Dj, 则保留点Dj; 否则保留点Di。
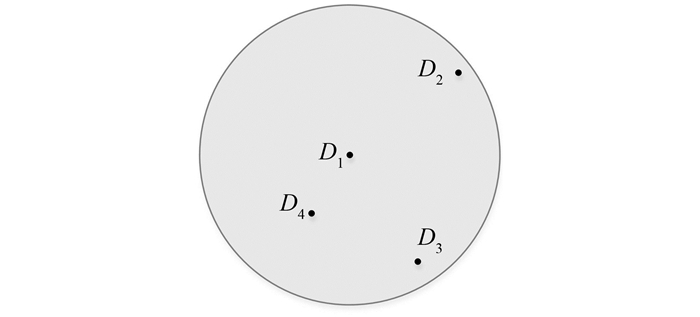 |
| 图 4 点集抽稀规则示意图 Fig.4 Diagram of the Point Set Diluting Rule |
3) 保留边界范围A与边界范围B的并集U(其中U=A∪B)。
4) 读取下一个边界范围, 回到步骤1)。
2 试验与分析基于上述的边界搜索算法, 提取北方海域某测区的水深离散点集的区域边界。边界范围内共有30 685个点, 用时2.1 s。其提取结果如图 5所示。采用经纬度差值为0.000 11(图 5中水深点间距0.6 cm, 换算成经纬度差约为0.000 11)、0.000 22、0.000 55作为抽稀阈值, 分别使用基于边界搜索的水深抽稀算法和基于网格的逐点抽稀算法, 对多波束水深数据进行抽稀处理, 分别得到抽稀水深结果, 水深数据处理部分结果如图 6所示。其中, 图 6(a)为基于网格的逐点抽稀, 点1深度抽稀阈值为0.000 22, 点2深度抽稀阈值为0.000 55;图 6(b)为基于边界搜索的抽稀, 深度范围1抽稀阈值为0.000 22, 深度范围2抽稀阈值为0.000 55。
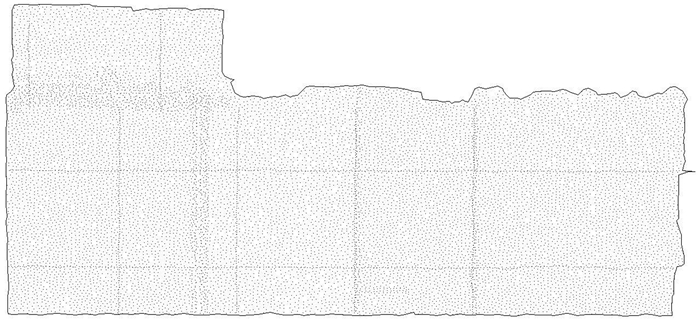 |
| 图 5 水深边界提取结果图 Fig.5 Results of Marine Data Boundary Extraction |
 |
| 图 6 两种方法的水深抽稀结果对比图 Fig.6 Result Comparison Diagram of Two Methods |
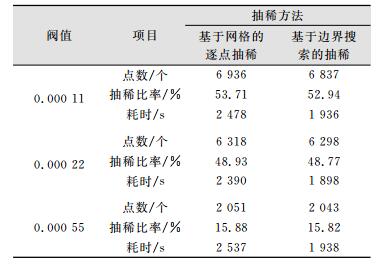
将采用不同方法和不同抽稀阈值得到的抽稀结果进行统计比对[14], 统计结果如表 1所示。
| 表 1 不同方法的水深数据抽稀结果对比 Tab.1 Diluting Results Comparison of Marine Data Within Different Methods |
 |
通过对比分析试验结果以及统计数据, 可以得出以下结论:
1) 应用本文所提出的基于边界搜索的水深抽稀方法进行多波束水深数据的抽稀, 保留下的水深点具有时效性, 试验结果达到了预期的目的。
2) 基于网格的逐点抽稀方法效率要低于基于边界搜索的抽稀方法的效率。
3) 水深抽稀结果和抽稀值密切相关。抽稀阈值越小, 保留的水深点越多, 抽稀比越大, 地形信息保留的越完整。
基于网格的逐点抽稀方法, 根据整个处理范围, 建立空间网格, 在无形中增加许多空网格的处理, 影响数据抽稀效率。由于网格的划分, 增加了一些数据处理的误差, 无法有效处理两个网格之间的数据冗余和数据空洞现象, 导致一些区域十分冗杂或者十分空洞。而基于边界搜索的抽稀方法是根据水深离散点集的空间边界范围来进行处理, 能够将空间处理范围进一步缩小, 大大减少了空间处理的复杂程度, 而且在点与点的处理上, 通过建立缓冲区比较测量时间和水深点深度值的方法, 能够更加有效地保留水深的时效性和可用性。因此, 通过以上对比分析可以看出, 基于边界搜索的抽稀方法能够在效率和准确率上优于基于网格的逐点抽稀方法[15]。
3 结束语海量水深数据的抽稀结果, 对航海安全性以及海洋生产快速制图都有着十分重要的影响。而抽稀方法的不同, 直接影响水深数据抽稀的结果。本文提出了基于边界搜索的海量水深数据抽稀方法, 通过确定离散水深点集的空间搜索边界, 对边界内的水深数据进行基于时间和空间范围的抽稀, 并与基于网格的逐点抽稀算法进行比较。通过对比和分析利用两种方法进行水深数据抽稀的实验结果可以看出, 基于边界搜索的水深数据抽稀算法能够在保留海底地形基本特征信息的前提下, 提高水深数据抽稀的效率以及准确性, 适用于海量水深数据的筛选, 有利于高效组织管理水深数据, 促进海事快速制图。但是该算法在水深离散数据边界搜索的过程中存在一定的缺陷, 例如, 对于边界空洞、R-shape或者是较为分散的点集, 在边界搜索的过程中会丢失部分空间边界特征, 影响到边界范围内的水深抽稀处理过程, 丢失某些水深特征信息, 不能得到满意的结果。在后续研究中考虑完善水深离散点集的边界提取方法, 得到更加合理的抽稀结果, 提高多波束测深数据抽稀的准确性。
| [1] |
吴超, 殷晓冬, 张立华, 等. 基于不确定度的多波束测深数据质量评估方法[J]. 海洋测绘, 2009, 29(5): 11-14. DOI:10.3969/j.issn.1671-3044.2009.05.004 |
| [2] |
曹鸿博, 张立华, 朱穆华, 等. 海量多波束数据抽稀方法的比对分析[J]. 海洋测绘, 2010, 30(5): 81-83. DOI:10.3969/j.issn.1671-3044.2010.05.023 |
| [3] |
王德刚, 叶银灿. CUBE算法及其在多波束数据处理中的应用[J]. 海洋学研究, 2008(2): 82-88. DOI:10.3969/j.issn.1001-909X.2008.02.012 |
| [4] |
夏伟, 黄谟涛, 刘雁春, 等. 多波束测深数据抽稀准则研究[J]. 测绘科学, 2010, 35(S1): 17-19. |
| [5] |
夏伟, 黄谟涛, 刘雁春, 等. Douglas-Peucker算法在多波束测深数据抽稀中的应用[J]. 测绘科学, 2009, 34(3): 159-160. |
| [6] |
焦永强. 多波束的校准方法及其成果分析[J]. 测绘地理信息, 2014, 39(6): 10-13. |
| [7] |
Graham R. An Efficient Algorithm for Determining the Convex Hull of a Finite Planarse[J]. Information Processing Letters, 1972, 1(1): 132-133. |
| [8] |
陈涛, 李光耀. 平面离散点集的边界搜索算法[J]. 计算机仿真, 2004(3): 21-23. DOI:10.3969/j.issn.1006-9348.2004.03.008 |
| [9] |
黄先锋, 程晓光, 张帆, 等. 基于边长比约束的离散点准确边界追踪算法[J]. 武汉大学学报·信息科学版, 2009, 34(6): 688-691. |
| [10] |
李雯静, 李少宁, 邱佳, 等. 凸壳内缩法进行多密度离散点群边界检测[J]. 测绘科学, 2014, 39(9): 126-129. |
| [11] |
Sampath A, Shan J. Building Boundary Tracing and Regularization from Airborne Lidar Point Clouds[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(7): 805-812. DOI:10.14358/PERS.73.7.805 |
| [12] |
眭海刚, 张光华, 卢之杰, 等. 海量多波束水深数据快速处理及质量检查方法[J]. 人民长江, 2008(6): 18-20. DOI:10.3969/j.issn.1001-4179.2008.06.007 |
| [13] |
黄冬梅, 季丽伟, 袁小华, 等. 基于时空一体化的海洋大数据快速展示平台[J]. 海洋环境科学, 2015, 34(5): 743-748. |
| [14] |
傅仲良, 吴建华. 多比例尺空间数据库更新技术研究[J]. 武汉大学学报·信息科学版, 2007, 32(12): 1 115-1 118. |
| [15] |
朱庆, 李德仁. 多波束测深数据的误差分析与处理[J]. 武汉测绘科技大学学报, 1998, 23(1): 1-4. DOI:10.3321/j.issn:1671-8860.1998.01.001 |
 2018, Vol. 43
2018, Vol. 43

