| SDP4模型用于北斗导航卫星轨道预报的精度分析 |
2. 信息工程大学,河南 郑州,450001;
3. 61081部队,北京,100094
2. Information Engineering University, Zhengzhou 450001, China;
3. 61081 Troops, Beijing 100094, China
北斗卫星导航系统 (BeiDou navigation satellite system, BDS) 是我国自主建设、独立运行,并与世界其他卫星导航系统兼容的全球卫星导航系统。北斗导航系统星座由地球静止轨道卫星 (geosynchronous earth orbit,GEO)、倾斜轨道同步卫星 (inclined geosynchronous satellite orbit,IGSO) 和中高轨卫星 (medium earth orbit,MEO)3类卫星构成[1, 2]。为了对卫星进行监测,需要预报卫星的位置。目前较常用的计算卫星位置的方法包括广播星历及历书。由广播星历计算出的卫星位置精度较高,可以用于导航卫星的定位定速计算;历书只提供基本的轨道参数,其位置预报精度也可长时间保持在公里级,但广播星历及历书的误差会随时间迅速增大[3]。
刁宁辉等基于双行元 (two-line element,TLE) 轨道根数进行了Terra卫星轨道计算[4];刘卫等进行了SGP4/SDP4(simplified general perturbations version 4/ simplified deep-space perturbations version 4) 模型预报可靠性分析,并提出了基于该模型进行低、中、高轨卫星预报误差无显著放大圈数[5];韩蕾等分析了基于SGP4/SDP4模型进行空间碎片轨道预测的精度分析,并验证该模型满足一定精度,可以用于空间碎片的轨道预测和初步威胁评估[6];刘一帆分析了北美空防司令部 (North American Aerospace Defense Command,NORAD) 双行元轨道预报模型,采用历元状态滤波建立了星上自主中长期轨道预报方法, 并以太阳同步轨道卫星为例对算法进行了仿真验证[7];李斌等针对北斗卫星分析了不同数据源对于其定轨精度的影响[8]。但是目前缺乏利用SDP4模型对不同种类 (GEO、IGSO、MEO) 的北斗导航卫星进行轨道预报的精度分析。
本文基于以上现状,利用从AGI数据库中获得的北斗TLE双行星历[9],基于SDP4模型,对北斗导航卫星进行轨道预报,对比德国波茨坦地学研究中心 (Helmholtz-Centre Potsdam-German Research Centre for Geosciences, GFZ) 公布的北斗卫星精密星历,评估其预报精度,并与其他常见的轨道预报方法进行了对比与分析。
1 TLE双行星历解析轨道预报模型不需要数字积分就可以给出任意时刻的轨道信息,具有比较小的运算量。广泛应用于航天器自主导航和中长期轨道预报的解析轨道预报模型是NORAD开发的双行轨道预报模型,该模型具有较高的中长期轨道预报精度。NORAD开发了用于传输开普勒轨道根数的TLE。TLE轨道根数是一组用于确定空间目标位置和速度的轨道数据,它由两行组成。例如,北斗MEO3(PRN11) 卫星的TLE轨道根数如表 1所示。其含义如下:1为第一行;38250表示空间目标编号;U为保密标识符;12018为国际标识符,12为发射年度2012年,018为该年度的发射序列,A代表部件序列号,如果出现AB代表一箭双星,依此类推;14258.77409为历元时刻,14表示2014年,后面的258.77409表示年积日的天数和不足一天的时间;-0.000 000 12和00000-0分别表示平动一阶导数和平动二阶导数;10000-3为BSTAR阻力系数;0为轨道计算模,7 582为星历号。2为第二行;38250意义同上;55.579 2表示轨道倾角 (°);88.011 6为升交点赤经 (°);23 652为轨道偏心率,小数点在首位并且省略;196.176 3为近地点角距 (°);158.342 5为平近点角 (°);1.862 334为平均运动角速度 (圈/d);16347为校验和。
| 表 1 北斗MEO3(PRN11) 卫星的TLE星历 Table 1 TLE Ephemeris of BDS MEO3 (PRN11) Satellite |
 |
2 SDP4模型轨道预报算法
TLE双行轨道预报模型中最常见的是SGP4/SDP4。SGP4模型由Ken Kuhlman开发,适用于近地航天器的轨道计算,SDP4模型是SGP4模型的外延,适用于深空目标。
SGP4可以准确地对于周期小于225 min的空间目标轨道进行预报,SDP4主要进行高轨和深空目标的轨道预报。SDP4模型运算量小,包含了日月引力、大气阻力、地球非球形引力摄动等影响,具有较高的中长期轨道预报精度。
为了基于SDP4模型进行计算,需要指定计算起始历元、计算结束历元和计算步长。然后读取TLE双行星历中的轨道数据,其计算步骤如下[10]:①引入基本参数系统;②利用TLE根数恢复出平根数;③由平根数计算长期项、长周期项、短周期项;④计算空间点的位置与速度。
3 数据分析利用北斗卫星的TLE双行星历,采用SDP4模型进行卫星轨道外推。设定2014年9月16日0:0:0.00(GPS时) 为分析起始时刻T0。从分析起始时刻开始,计算并预报10日的轨道。计算程序基于Matlab/STK接口进行二次开发,设置计算步长为6 s,卫星姿态为太阳帆板面垂直指向太阳,卫星Z轴 (天线方向) 指向地心,设定该预报出的轨道为分析轨道
从IGS的MGEX数据库中下载由GFZ公布的北斗卫星精密星历 (2014年9月16日至26日,文件为gbm18102.sp3z至gbm18115.sp3),称其为参考轨道
计算出分析轨道
需要将分析轨道
为了准确地跟踪卫星,必须保证天线的指向角度正确,因为天线的指向直接影响着信号的强度。对于高增益转台7.5 m天线而言,它的半功率波束宽度约为1.7°。
根据以上条件,MEO卫星距离地面高度大约为20 000 km,监测站天线为了实现对于MEO卫星的预报和监测,卫星轨道预报误差dr不能超过296 km。由于IGSO和GEO卫星的轨道高度更高,所以dr也可以满足对于该两类卫星的预报和监测。
3.2 北斗MEO卫星轨道预报首先分析MEO3(PRN11) 号卫星,该卫星TLE星历如表 1所示,该星历参考时刻为2014年9月15日18时 (UTC),预报从分析起始时刻T0开始的10 d的轨道。在相同时段内将参考轨道
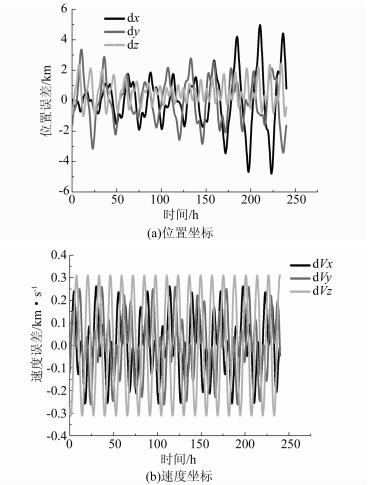 |
| 图 1 北斗MEO卫星预报10 d卫星位置和速度坐标分量误差 Figure 1 Coordinate Components Differences of Position and Velocity for BDS MEO's 10 Day Prediction |
从图 1(a)可以看出,该卫星预报的位置坐标分量误差随时间逐渐增大,但是并没有明显扩大。预报175 h以内的轨道的坐标分量误差小于3 km,预报175 h之后误差开始扩大,但是仍能控制在5 km以内。
从图 1(b)可以看出,该卫星预报的速度坐标分量误差随时间变化较为均匀,并没有明显的误差积累或者放大,各方向均小于0.3 km/s。
3.3 北斗IGSO卫星轨道预报分析IGSO3(PRN08) 号卫星,该卫星TLE星历如表 2所示 (表中各指标含义同表 1),该星历参考时刻为2014年9月15日7时 (UTC)。预报从分析起始时刻T0开始的10 d的轨道[10-12]。
| 表 2 北斗IGSO3(PRN08) 卫星的TLE轨道 Table 2 LE Ephemeris of BDS IGSO3(PRN08) Satellite |
 |
从图 2(a)可以看出,该卫星预报3 d (72 h) 内位置坐标分量误差均小于4 km,但是预报80 h后误差迅速扩大。从图 2(b)可以看出,预报的速度误差变化较为均匀,并没有明显的误差积累或者放大,X和Y方向均小于0.125 km/s,Z方向小于0.25 km/s。
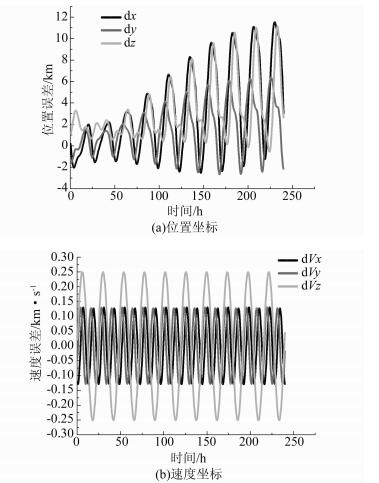 |
| 图 2 北斗IGSO卫星预报10 d卫星位置和速度坐标分量误差 Figure 2 Coordinate Components Differences of Position and Velocity for BDS IGSO's 10 Day Prediction |
3.4 北斗GEO卫星轨道预报
分析GEO6(PRN02) 号卫星,该卫星TLE星历如表 3所示,该星历参考时刻为2014年9月15日2时 (UTC)。预报从分析起始时刻T0开始的10 d的轨道。
| 表 3 北斗GEO6(PRN02) 卫星的TLE轨道 Table 3 TLE Ephemeris of BDS GEO6(PRN02) Satellite |
 |
从图 3(a)可以看出,该卫星预报的位置坐标分量误差只有在24 h内误差小于2 km,之后随时间迅速扩大。
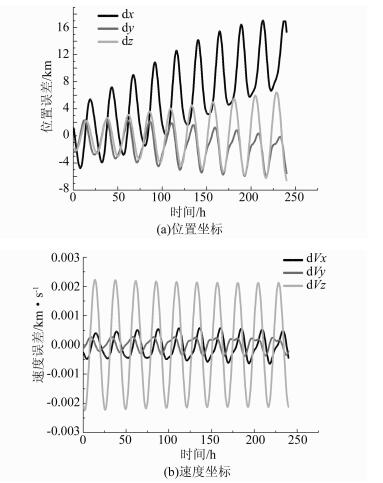 |
| 图 3 北斗GEO卫星预报10 d卫星位置和速度坐标分量误差 Figure 3 Coordinate Components Differences of Position and Velocity for BDS GEO's 10 Day Prediction |
从图 3(b)可以看出,由于GEO卫星相对于地球静止,所以在WGS84地固坐标系下,GEO卫星预报的速度坐标分量误差比较小,但是Z方向误差明显大于X、Y方向误差。
精密星历利用历元时刻附近的观测数据,对卫星摄动和空间环境参数进行估计,因而测量估计出的该参数具有更高精度,所以其积分得出的轨道在观测时间段内具有更高的精度。对比发现,由于卫星所处的空间环境时刻复杂变化,卫星太阳能帆板反射系数会随时间和空间环境的变化造成光压无法精确描述,卫星姿态误差会引起面质比参数的变化,造成光压和阻力摄动误差,这些都会造成SDP4模型利用平根数预报的轨道同精密轨道相比会产生随时间积累的误差。
3.5 SDP4模型、HPOP模型、历书轨道预报比较将北斗MEO3卫星 (PRN11) 设置为分析卫星,分别把采用Trimble公司发布的接收机历书星历、基于HPOP模型预报出的轨道和基于SDP4模型预报出的轨道进行对比。其中,HPOP模型的起始条件设置为基于SDP模型计算的起始时刻T0的轨道坐标。
对比区间为2014年9月16日0:0:0.00至26日0:0:0.00,时间系统为GPS时,在WGS84坐标系下,将3种方法计算出的结果同GFZ公布的精密星历比较,分别求出三维位置误差,其随时间变化的曲线如图 4所示,横坐标表示从起始时刻T0开始的轨道预报时间,历元间隔15 min,纵坐标表示三维位置误差。
 |
| 图 4 3种方法轨道外推的三维位置误差比较 Figure 4 Differences of Positions for Three Methods of Orbit Prediction |
基于HPOP模型进行轨道预报的初始条件为:时间系统为GPST时,T0为2014年9月26日0:0:0.00,历元时刻X坐标为-7 478.420 363 km,Y坐标为-24 669.002 475 km,Z坐标为10 556.591 609 km,历元时刻速度Vx为0.087 297 km/s,Vy为-1.208 146 km/s,Vz为-2.775 523 km/s,反射系数Cr设为1,面质比A/M设为0.02。
从图 4可以看出,HPOP高精度轨道外推模型预报两日 (48 h) 效果最好,SDP4模型和历书星历次之。但是从75 h之后,HPOP模型和历书星历的轨道外推误差会迅速变大,尤其以历书星历比较明显,而SDP4模型还能保持一定的精度。因此,在短期 (75 h) 轨道预报中,3种方法均可以采用,但是75 h以上的轨道预报应当采用SDP4模型。这主要因为HPOP模型采用的摄动力模型比较复杂,可比较真实地仿真短时间内的卫星受力情况,而SDP4模型采用平根数,可恢复较长时间后的卫星受力情况。
对于3种方法实现的短期轨道预报,都可以应用于北斗接收机的自主星历预报,以实现接收机对卫星的捕获,但是只有利用SDP4模型的半个月左右的中长期预报可以应用于地面监控站对于北斗卫星高度角和方位角的预测,以捕获卫星来实现对卫星的监控。
为了比较程序运行效率,在HPZ620工作站 (CPU为Xeon E5-1620,主频3.6 GHz) 上运行轨道预报程序,其中HPOP模型和SDP4模型都基于Matlab平台调用Matlab/STK接口,计算步长都设置为6 s,历书星历采用Trimble星历预报软件进行计算。计算区间为2014年9月16日0:0:0.00至26日0:0:0.00(GPS时)。
利用SDP4模型的外推程序计算所需时间为10.2 s,HPOP模型为25.8 s,历书星历计算时间小于1 s。由于HPOP模型考虑了多种摄动力且模型复杂,所以其计算时间明显最长,但是这也印证了其在短期轨道预报中精度最高;历书星历只考虑最简单的根数,所以计算速度最快;SDP4模型计算速度居中。
4 结束语通过实验可以看出,SDP4模型计算速度快,可以应用于北斗导航卫星的轨道预报,满足对卫星监测的精度要求。该模型对于MEO卫星轨道预报效果最好,外推10日的位置坐标分量误差小于5 km,速度坐标分量小于0.3 km/s;对于IGSO卫星预报效果次之,外推3日的位置坐标分量小于5 km,外推10日小于18 km,速度坐标分量小于0.3 km/s;GEO卫星轨道预报效果最差,外推1日后的位置坐标分量误差会迅速放大,超过10 km,由于本文采用地固坐标系,所以其预报速度的坐标分量误差不大。3日以内的短期轨道预报可以采用HPOP高精度轨道外推模型或者是历书,但是3日以上的轨道预报采用SDP4模型更好。由于本文只选用了来源于AGI数据库的北斗TLE星历,所以后续研究可以分析不同来源的TLE星历或者是利用精密星历拟合出的TLE星历的轨道预报精度。
| [1] |
李作虎. 卫星导航系统性能监测及评估方法研究[D]. 郑州: 信息工程大学, 2012 |
| [2] | 谭述森. 卫星导航定位工程[M]. 北京: 国防工业出版社, 2010 |
| [3] | 余小游, 覃曼丽, 吴问其, 等. 基于SDP4模型的导航卫星仰角及方位角预报[J]. 全球定位系统, 2014, (3): 44–48 |
| [4] | 刁宁辉, 刘建强, 孙从容, 等. 基于SGP4模型的卫星轨道计算[J]. 遥感信息, 2012, 27(4): 64–70 |
| [5] | 刘卫, 缪元兴. SGP4/SDP4模型预报可靠性分析[J]. 天文研究与技术, 2011, 8(2): 128–131 |
| [6] | 韩蕾, 陈磊, 周伯昭. SGP4/SDP4模型用于空间碎片轨道预测的精度分析[J]. 中国空间科学技术, 2004, 24(4): 65–71 |
| [7] |
刘一帆. 基于SGP4模型的低轨道航天器轨道预报方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009 |
| [8] | 李斌, 李郭超, 李耿浩. 不同数据源对卫星定轨精度的影响分析[J]. 测绘地理信息, 2014, 39(2): 69–72 |
| [9] | AGI.The AGI Products[DB/OL].[2015-01-01].http://www.agi.com/products |
| [10] | IGS. The MGEX Product[EB/OL].[2015-01-01].http://igs.org/mgex/products |
| [11] | 秦顺友, 许德森. 卫星通信地面站天线工程测量技术[M]. 北京: 人民邮电出版社, 2006 |
| [12] | 丁 溯泉, 张 波, 刘 世勇. STK在航天任务仿真分析中的应用[M]. 北京: 国防工业出版社, 2011 |
 2017, Vol. 42
2017, Vol. 42

