| 基于GIS极坐标的丹顶鹤野外调查定位方法 |
2. 江苏省地理环境演化国家重点实验室培育建设点,江苏 南京,210023;
3. 江苏省地理信息资源开发与利用协同创新中心,江苏 南京,210023
2. State Key Laboratory Cultivation Base of Geographical Environment Evolution, Jiangsu Province, Nanjing 210023, China;
3. Application, Nanjing 210023, China
栖息地与生境保护是丹顶鹤就地保护的重要内容。目前,大量的研究往往结合丹顶鹤的栖息地调查而进行[1-3]。但是,栖息地的研究由于缺乏空间分布的精细定位数据,从而限制了包括丹顶鹤在内的鸟类物种生境质量的细致研究。因此,野外调查中如何精确定位丹顶鹤的空间分布点,是丹顶鹤栖息地和生境保护需要解决的重要科学问题之一。
目前,野生动物研究中空间分布信息获取的手段主要有GPS[4]、无人机技术[5]、红外触发相机[6]、隐蔽摄像机[7]等。这些方法都有各自的使用范围和定位精度,从时效性、经济性和定位精度方面又都有各自的不足。丹顶鹤是警惕性很高的动物,在野外观察距离小于200 m时会显著增加警戒频次[8]。常规方法(如占用丹顶鹤位置用GPS定位)会干扰丹顶鹤的正常活动,连锁警戒效应对其他鸟类的活动也会产生较大的干扰,且对于不可达区域(如潮沟的阻隔)只能粗略地估算或舍弃活动点,造成误差增大和信息缺失,不能满足丹顶鹤活动空间分布研究的需求。本文基于极坐标的定位原理,运用GIS软件对丹顶鹤空间分布定位技术进行了研究,并对其可行性和精度进行了探讨。
1 定位方法设计极坐标定位是通过测定待定点到至少一个已知点的距离和方位所进行的一种定位。目前,极坐标定位已经广泛运用于数控[9]、医学研究[10, 11]、道路桥梁的施工放样以及工程变形监测[12, 13]等领域。极坐标定位数据包括基准点的位置、距离参数、方位角参数。基准点的位置信息可由手持GPS获取,距离参数可由测距仪器获取,方位角参数可由望远镜获取,从而满足了极坐标定位的条件,具备了理论可行的基础。
本文使用到的调查设备有激光测距仪(TruPulse360)、手持GPS(Tirmble JunoSA)、望远镜(Boshile),使用到的软件有ArcGIS 10、Excel 2016、IBM SPSS Statistics 19等。
在丹顶鹤调查过程中,与丹顶鹤保持一定的距离,利用手持GPS在观测位置(基准点)进行定位,通过激光测距仪测得基准与丹顶鹤位置之间的距离,利用望远镜测得望远镜极轴与观测线之间的夹角(方位角)。望远镜与ArcGIS的方位角不一致的问题可通过验证点改正方位角来解决,从而可以在ArcGIS中对丹顶鹤的位置进行确定。
2 定位精度分析 2.1 精度验证的设计首先,将GPS定位点与ArcGIS估算出的目标点进行位置对比,两点之间的偏移距离为总体估算误差;然后,在ArcGIS中测量基于GPS的距离和角度,并与野外采集的距离和方位角进行对比,得出对测距仪的测距误差和望远镜的测角误差。
2.2 外业数据采集数据采集区域为盐城国家级珍禽自然保护区核心区,地点为中心观鸟台。数据采集人员4名,分别是观测员、记录员、指挥员、流动定位人员。
1) 在基准点的观测员用GPS测得基准点的经纬度位置数据,数据记录完成后将GPS交给流动定位人员,流动定位人员走到A1点,并用GPS在A1点定位。
2) 观测员在基准点用望远镜测得A1点相对于基准点的方位角θ1,用测距仪测得基准点与A1点之间的距离D1。记录员记录方位角和距离数据。
3) 指挥员向流动定位人员发出记录完成信号,流动定位人员接到信号后行走至A2点,并用GPS在A2点定位。
4) 观测员在基准点用望远镜测得A2点相对于基准点的方位角θ2,用测距仪测得基准点与A2点之间的距离D2。记录员记录方位角和距离数据。
5) 流动定位人员接到指挥员的记录完成信号后,行走至A3点,并用GPS在A3点定位。
依次对目标点定位所需的D、θ和GPS定位数据进行采集。
本次精度验证共采集36个定位点,其中B1、B2作为基准点,A4、A16、A17和A24(考虑到方位角改正的均匀性)为方位角改正的参照点;A1~A28的定位基点为B1,A29~A34的定位基点为B2。
2.3 内业数据整理1) GPS定位数据整理。将手持GPS采集的数据写入后导入ArcGIS中,定义投影后得到GPS定位点。
2) 方位角的改正。由于望远镜和ArcGIS的极轴不一致,外业望远镜采集的θ不能直接用于目标位置的确定。在ArcGIS中根据距离和方向创建点要素的编辑工具可测量A4、A16、A17、A24等4点的方位角,以此来进行方位角改正。ArcGIS以正东方向为极轴,逆时针为正方向,望远镜方位角是北偏东,以顺时针为正方向。望远镜测出的方位角为θ,设用于绘图的改正方位角为γ,在ArcGIS中测得改正参照点的方位角为η,望远镜的极轴与ArcGIS极轴之间的夹角为α,如图 1所示。
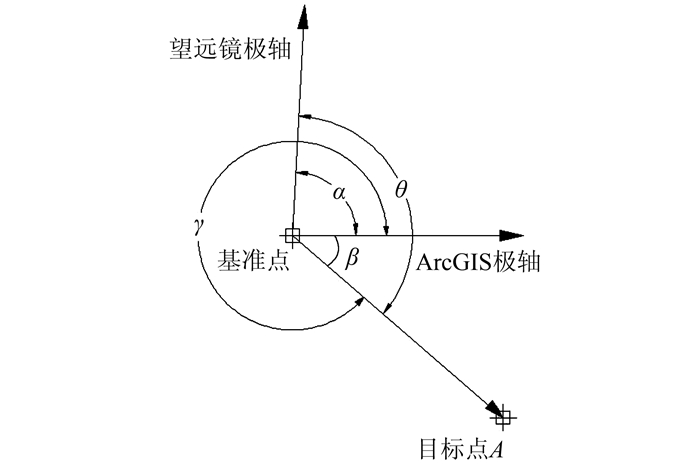 |
| 图 1 方位角改正示意图 Fig.1 Diagram of Azimuth Correction |
对于同一望远镜来说,其极轴与ArcGIS极轴夹角α在理论上是不变的。因此,只需利用几个参考点求出α,便可对其他目标点进行方位角改正,由图 1可以推出方位角的改正公式为γ=360°-θ+α,其中,α=η+θ-360°。
本次验证A4、A16、A17、A24作为参照点,在ArcGIS中测得的基于GPS定位的方位角η4、η16、η17和η24分别为67.506°、135.767°、251.700°和338.671°,求出α4、α16、α17和α24分别为93.306°、94.667°、94.900°和92.971°,平均值=93.961°,则此次方位角改正公式为γ=360°-θ+ =453.961°-θ。
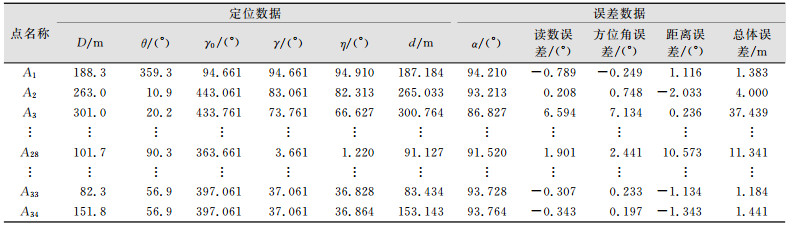
在Excel中用改正公式对方位角进行改正,得到γ0, 对大于360°的角度减去360°,得到改正方位角γ。同时在ArcGIS中利用距离和方向添加点要素工具测量基于GPS的所有点的距离参数(d)和方位角参数(η),得到的数据如表 1所示。
| 表 1 定位数据和误差数据统计 Tab.1 Statistics of Location Data and Errors |
 |
3) 位置估算。在ArcGIS中利用γ和D进行点要素的创建。估算出的位置点以C命名,结果如图 2所示。
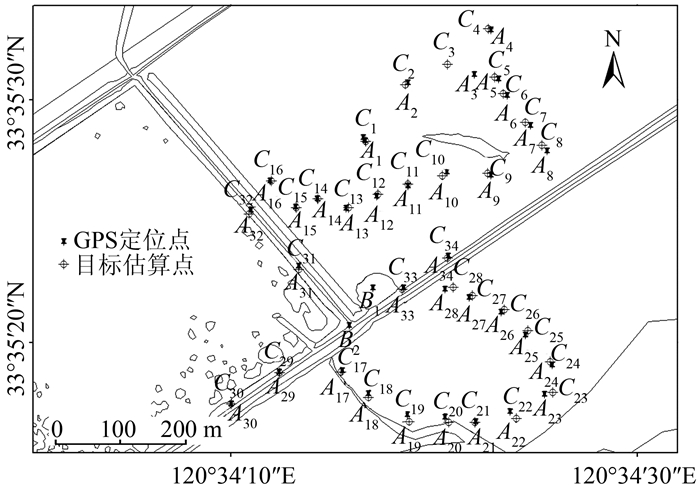 |
| 图 2 估算点与GPS定位点分布图 Fig.2 Distribution of GPS Points and Estimation Points |
3 精度评价 3.1 误差数据的生成
误差出现的原因主要有测距仪的测距误差和望远镜方位角误差。总体误差是用估算点C和GPS定位点A之间的距离来衡量的,距离误差以D-d的差值来衡量,方位角误差以γ-η的差值来衡量。此外,方位角改正参照点的选取也会影响参考改正角α的大小,从而对望远镜方位角误差产生影响,所有点计算的α与4个点的α的差值可以作为方位角选取的误差;若以α作为基准,它与每个点对应的α值相减,可作为望远镜读数不稳定产生的误差。误差数据见表 1。
由表 1可以看出,A3和A28两点的总体误差与测量距离的比值超过10%,认为A3与A28的定位数据异常,在本次精度评价中将其剔除。方位角误差、读数误差中有负值,在描述性统计分析中会影响均值,从而使误差均值减小,导致精度偏高,因此,在以下误差评价中,以误差的绝对值作为描述性统计分析的对象。
3.2 误差评价将表 1中的误差数据取绝对值后导入到SPSS中进行描述性统计分析,结果如表 2所示。
| 表 2 误差绝对值描述性统计 Tab.2 Statistics of Absolute Errors |
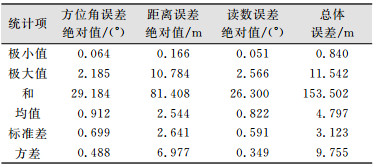 |
理想状况下γ与η相等,但是由于α改正参照点的选择和望远镜方位角读取产生的误差使得改正方位角产生偏差。由表 2可知,方位角的误差平均值为0.912°,而望远镜的测角精度为1°,因此,方位角产生的误差数值较小。在极坐标定位方法中,方位角误差在近距离测量中对总体误差影响较小,随着测量距离的增大,总体误差也增大。角度误差对总体误差的影响需根据测量距离来衡量。
在ArcGIS中,可以用测地线测量基准点B与目标点A之间的距离d对距离误差D-d的绝对值进行描述性统计。由表 2可知,测距仪的测距误差平均为2.544 m,最高达到了10.784 m,而测距仪测量的标称精度为±1 m,由此可知,在测距仪使用过程中产生的误差较大。值得注意的是,总体误差总是大于距离误差。因此,在近距离和中距离定位中应特别注意减少测距误差。
方位角改正过程中用到的α在理想状况下为定值。但是由于望远镜读数和GPS定位偏移等原因造成α并不是一个定值,而且改正参照点的选取也会产生改正方位角误差。32个点的α=93.421°,而4个改正参照点的α=93.961°,两者差值为0.540°,为方位角改正点选取误差。若以32个点的α=93.421°作为基准,它与每个点对应的α值相减,可作为望远镜读数不稳定产生的误差。由表 2读数误差的绝对值描述性统计可知,望远镜读数误差的平均值为0.822°,最大为2.566°,可见在方位角误差中的望远镜读数误差(0.822°)大于方位角改正点选取产生的误差(0.540°)。因此,在运用此方法时,除了要合理选取方位角改正参照点之外,还应该注意读数的准确性与稳定性。
从表 2还可知,总体误差的累计值为153.502 m,表 1中的测量距离D的累计值为6 091 m,累计误差比距为2.52%。
综上所述,本文方法用于野生动物定位调查是可行的,能够满足丹顶鹤等体型较大的野生动物活动区域调查需求。
4 误差影响因子与总体误差的相关性分析将各误差的绝对值和各误差导入到SPSS中做双变量相关性分析,结果如表 3所示。
| 表 3 误差绝对值和误差与影响因子相关性分析 Tab.3 Correlation Analysis of Absolute Errors, Errors and Impact Factors |
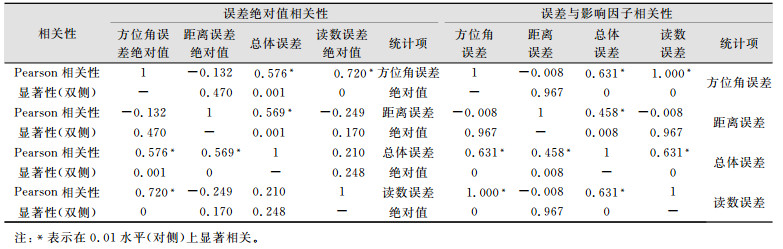 |
由表 3误差绝对值相关性可以看出:①距离误差的绝对值和方位角误差的绝对值都与总体误差显著相关,方位角误差绝对值的Pearson相关系数大于距离误差绝对值,读数误差是造成方位角误差的主要因素;②距离误差、方位角误差和读数误差都与总体误差显著相关,方位角误差与总体误差的Pearson相关系数(0.631)大于距离误差与总体误差的Pearson相关系数(0.458),读数误差和方位角误差与总体误差的显著性和Pearson相关系数都相同,读数误差与方位角误差线性相关。
从表 3误差与影响因子相关性可以看出,方位角误差与总体误差的相关性大于距离误差与总体误差的相关性。
综合以上分析,读数误差与总体误差没有相关性,这显然与实践经验相悖,可能是绝对值影响了其与总体误差的相关性分析结果,因此, 除去绝对值对各误差做相关性分析。
5 结束语本文利用ArcGIS软件结合极坐标定位法对丹顶鹤定位方法进行了可行性验证,对定位精度以及对定位误差的影响因素进行了数据分析。分析结果表明,本文方法用于野生动物定位调查是可行的,能够满足丹顶鹤等体型较大的野生动物活动区域调查需求。在测距仪使用过程中产生的误差较大,而且总体误差总是大于距离误差,因此,在近距离和中距离定位中应特别注意减少测距误差。在相关性分析中,距离误差、方位角误差和读数误差都与总体误差显著相关,方位角误差的影响对整体误差的影响大于距离误差, 方位角误差是影响定位精度的最主要因素。因此,在实际运用时,要特别注意方位角误差的控制,除了要合理选取方位角改正参照点之外,应特别注意读数的准确性与稳定性;在定位数据采集时,可以通过使用精度较高的测量仪器来减少总体误差。
| [1] |
王志强, 蒋丽, 刘贤赵, 等. 近30年来扎龙湿地丹顶鹤繁殖种群空间格局及动态[J]. 生态与农村环境学报, 2014, 30(1): 27-31. DOI:10.3969/j.issn.1673-4831.2014.01.005 |
| [2] |
肖洛斌, 张慧, 缪旭波. 盐城保护区生境变化与丹顶鹤数量的耦合关系分析[J]. 生态科学, 2014, 33(6): 1189-1193. |
| [3] |
郭殿繁, 臧淑英, 那晓东. 扎龙保护区丹顶鹤栖息地适宜性评价[J]. 地理与地理信息科学, 2015, 31(1): 54-58. DOI:10.3969/j.issn.1672-0504.2015.01.012 |
| [4] |
Harrington L A, Harrington A L, Hughes J, et al. The Accuracy of Scat Identification in Distribution Surveys: American Mink, Neovison Vison, in the Northern Highlands of Scotland[J]. European Journal of Wildlife Research, 2010, 56(3): 377-384. DOI:10.1007/s10344-009-0328-6 |
| [5] |
Christie K S, Gilbert S L, Brown C L, et al. Unmanned Aircraft Systems in Wildlife Research: Current and Future Applications of a Transformative Technology[J]. Frontiers in Ecology and the Environment, 2016, 14(5): 241-251. DOI:10.1002/fee.1281 |
| [6] |
何毅, 崔宁, 李中原, 等. 红外触发相机在野生动物调查中的应用——以北京小龙门地区为例[J]. 高校生物学教学研究(电子版), 2011, 1(2): 56-58. |
| [7] |
谢志刚.上海郊区狗獾(Meles meles)生态学研究[D].上海: 华东师范大学, 2011
|
| [8] |
Li Zhongqiu. Suitable Distance to Observe Red-crowned Cranes: A Note on the Observer Effect[J]. Chinese Birds, 2011, 2(3): 147-151. DOI:10.5122/cbirds.2011.0020 |
| [9] |
白大鹏, 李玉昆, 李楠. 极坐标式数控机床的运动控制研究[J]. 燕山大学学报, 2008, 32(3): 206-208. DOI:10.3969/j.issn.1007-791X.2008.03.005 |
| [10] |
高翔, 包柏成. 极坐标测量方法在Twin-Block矫治下颌后缩疗效分析中的应用[J]. 口腔疾病防治, 2010, 18(11): 568-571. |
| [11] |
赵俊杰, 王林, 李青奕. 极坐标方法预测美貌人群软硬组织头影测量个体化特征的研究[J]. 口腔医学, 2011, 31(11): 662-666. |
| [12] |
丁林磊, 庞文, 万冠军. 小角法精确悬高测量方法研究[J]. 测绘地理信息, 2013, 38(6): 42-44. |
| [13] |
许文学, 羊远新, 李锋, 等. GPS配合全站仪在机场边坡变形监测中的应用[J]. 测绘地理信息, 2012, 37(6): 60-63. |
 2018, Vol. 43
2018, Vol. 43


