| 基于Romberg积分与牛顿迭代的高斯投影坐标正反算算法 |
2. 河北地质大学土地资源与城乡规划学院, 河北 石家庄, 050031
2. Institute of Land Resource and Urban and Rural Planning, Hebei GEO University, Shijiazhuang 050031, China
大地测量中,高斯投影正反算的问题关键是子午线弧长数学模型的解算和求解底点纬度Bf[1]。为了提高两者的计算精度、优化计算方法、简化编程或提高运算效率,相关学者提出许多计算方法。文献[2-7]分别引入了递归算法、递推公式、数值积分以及牛顿迭代、插值公式直接求解等方法,使得子午线弧长解算精度优于0.1 mm,底点纬度解算精度达到10-5(″)量级;文献[8, 9]提出基于第二类椭圆和依不同纬度变量的子午线弧长计算方法,丰富了子午线弧长计算的理论;文献[10]对子午线弧长公式的泰勒级数展开形式进行了简化和优化;文献[11-13]将计算子午线弧长与底点纬度视作求解一阶常微分方程,通过数值计算的方法进行求解,并对各种计算方法的解算精度、解算速度进行了分析与评价;文献[14]利用Excel的“单变量求解”功能实现底点纬度的免编程计算。
本文在综合考虑编程简洁性、运算速度和计算精度的基础上,根据文献[4]的研究思路设计了基于Romberg积分和牛顿迭代的高斯投影坐标正反算算法,并通过C#编程实现了高斯投影坐标正反算。
1 基于Romberg积分和牛顿迭代的高斯投影坐标正反算算法由已知大地坐标(B,L)计算高斯投影平面坐标(x, y):
| $ \begin{array}{l} x = X + \frac{N}{2}\sin B\cos B{l^2} + \frac{N}{{24}}\sin B{\cos ^3}B\left( {5 - {t^2} + 9{\eta ^2} + 4{\eta ^4}} \right){l^4} + \\ \;\;\;\frac{N}{{720}}\sin B{\cos ^5}B\left( {61 - 58{t^2} + {t^4}} \right){l^6} \end{array} $ | (1) |
| $ \begin{array}{l} y = N\cos Bl + \frac{N}{6}{\cos ^3}B\left( {1 - {t^2} + {\eta ^2}} \right){l^3} + \\ \;\frac{N}{{120}}{\cos ^5}B\left( {5 - 18{t^2} + {t^4} + 14{\eta ^2} - 58{\eta ^2}{t^2}} \right){l^5} \end{array} $ | (2) |
式中,X为自赤道量超至已知点的子午线弧长;N为卯酉圈半径,
高斯投影坐标反算公式为:
| $ \begin{array}{l} B = {B_f} - \frac{{{t_f}}}{{2{M_f}{N_f}}}{y^2} + \frac{{{t_f}}}{{24{M_f}N_f^3}}\left( {5 + 3t_f^2 + \eta _f^2 - 9\eta _f^2t_f^2} \right){y^4}\\ - \frac{{{t_f}}}{{720{M_f}N_f^5}}\left( {61 + 90t_f^2 + 45t_f^4} \right){y^6} \end{array} $ | (3) |
| $ \begin{array}{l} l = \frac{1}{{{N_f}\cos {B_f}}}y - \frac{1}{{6N_f^3\cos {B_f}}}\left( {1 + 2t_f^2 + \eta _f^2} \right){y^3} + \\ \frac{1}{{120N_f^5\cos {B_f}}}\left( {5 + 28t_f^2 + 24t_f^4 + 6\eta _f^2 + 8\eta _f^2t_f^2} \right){y^5} \end{array} $ | (4) |
式中,Bf为底点纬度,其余有下标的各量都是Bf的函数。当l < 3.5°时,上式换算精确达0.000 1″;B和l的单位为弧度。
在高斯投影坐标正反算中最为关键的是子午线弧长与底点纬度的计算。
1.1 子午线弧长的计算子午线弧长数学模型是计算从赤道到任意纬度B的平行圈之间的弧长:
| $ X = \int_0^B M {\rm{d}}B = a\left( {1 - {e^2}} \right)\int_0^B {{{\left( {1 - {e^2}{{\sin }^2}B} \right)}^{ - \frac{3}{2}}}} {\rm{d}}B $ | (5) |
式中,M为子午线曲率半径。
求解式(5)的传统算法[1]是把被积函数按级数展开,为便于积分将正弦函数的幂函数展开为余弦的倍数函数。积分后经整理为:
| $ X = {a_0}B - \frac{{{a_2}}}{2}\sin 2B + \frac{{{a_4}}}{4}\sin 4B - \frac{{{a_6}}}{6}\sin 6B + \frac{{{a_8}}}{8}\sin 8B $ | (6) |
式中,
| $ \left\{ {\begin{array}{*{20}{l}} {{a_0} = {m_0} + \frac{{{m_2}}}{2} + \frac{3}{8}{m_4} + \frac{5}{{16}}{m_6} + \frac{{35}}{{128}}{m_8}}\\ {{a_2} = \frac{{{m_2}}}{2} + \frac{{{m_4}}}{2} + \frac{{15}}{{32}}{m_6} + \frac{7}{{16}}{m_8}}\\ {{a_4} = \frac{{{m_4}}}{8} + \frac{3}{{16}}{m_6} + \frac{7}{{32}}{m_8}}\\ {{a_6} = \frac{{{m_6}}}{{32}} + \frac{{{m_8}}}{{16}}}\\ {{a_8} = \frac{{{m_8}}}{{128}}} \end{array}} \right. $ |
其中,m0=a(1-e2), m2=
式(6)中,
为求解式(5),本文采用Romberg积分方法。Romberg积分将积分区间逐次分半,得到低次复核梯形积分序列,然后运用Richardson外推算法加速收敛,并将得到的相邻两次结果进行比较,直到较差值小于要求的精度时为止[15, 16]。
1.2 底点纬度求解为求解Bf,用式(5)或式(6)构造关于Bf的一元方程:
| $ f\left( {{B_f}} \right) = a\left( {1 - {e^2}} \right)\int_0^{{B_f}} {{{\left( {1 - {e^2}{{\sin }^2}{B_f}} \right)}^{ - \frac{3}{2}}}} {\rm{d}}{B_f} - X $ | (7) |
| $ \begin{array}{*{20}{r}} {f\left( {{B_f}} \right) = {a_0}{B_f} - \frac{{{a_2}}}{2}\sin 2{B_f} + \frac{{{a_4}}}{4}\sin 4{B_f} - }\\ {\frac{{{a_6}}}{6}\sin 6{B_f} + \frac{{{a_8}}}{8}\sin 8{B_f} - X} \end{array} $ | (8) |
问题转化为求式(7)或式(8)方程的解,利用牛顿迭代算法进行求解[6, 15]。设已知方程f(x)=0有近似根xk(假定f′(xk)≠0),将函数f(x)在xk展开,有f(x)≈f(xk)+f′(xk)(x-xk),于是方程f(x)=0可近似地表示为f(xk)+f′(xk)(x-xk)=0,记其根为xk+1,则xk+1的计算式为:
| $ {x_{k + 1}} = {x_k} - \frac{{f\left( {{x_k}} \right)}}{{{f^\prime }\left( {{x_k}} \right)}}, k = 0, 1, 2, \cdots $ | (9) |
综上,求解式(7)或式(8)式一元方程解的牛顿迭代式为:
本文所述高斯投影坐标正反算算法的实现过程如下。利用Romberg积分算法求解式(5),得到子午线弧长X,然后将其代入式(1)、式(2)做高斯投影坐标正算;利用牛顿迭代算法求解式(7)(通过调用上述Romberg积分算法模块计算子午线弧长X),求得底点纬度并将其代入式(3)、式(4)做高斯投影坐标反算。
利用式(6)求解子午线弧长X,然后将其代入式(1)、式(2)做高斯投影坐标正算;同理,利用式(8)求解底点纬度,并将其代入式(3)、式(4)做高斯投影坐标反算。此为高斯投影坐标正反算的传统算法过程。
为了验证本文所提算法的有效性和正确性,利用C#编程实现算法。并以CGCS2000椭球(a=63 781 37 m, α=1/298.257 222 101)中央子午线为114°的一组模拟数据为例, 将其计算结果与传统算法进行比较,见表 1、表 2。大地坐标的输入及输出形式作如下说明:3°40′40.123 45″其形式为3.404 012 345。
| 表 1 高斯投影坐标正算结果比较 Tab.1 Comparison of Forward Calculation Results of Gaussian Projection Coordinates |
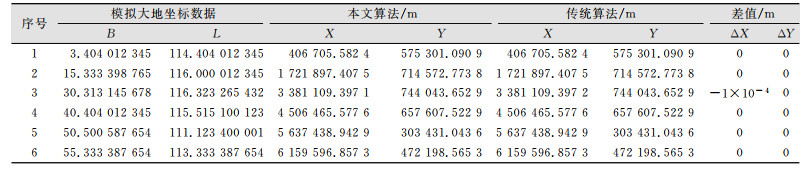 |
| 表 2 高斯投影坐标反算结果及其与初始模拟值之差 Tab.2 Difference Between the Intial Simulation Vaules and Results of Backward Calculation |
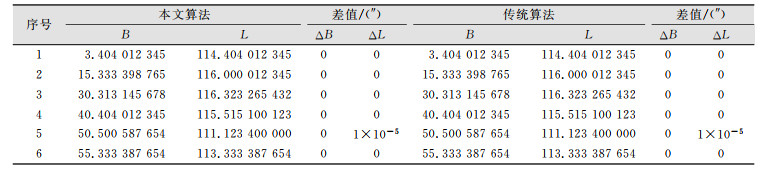 |
由表 1、表 2可知,高斯投影坐标正算达到1 mm以内的计算精度,高斯投影坐标反算的计算精度达到1×10-4(″)以内, 说明该算法精度与传统算法相当。
3 结束语Romberg积分在解算子午线弧长时涉及到的参数较少,省去多项式推导及大量系数的计算,因此该算法代码书写相对简洁,计算精度可扩展性比较强,不考虑多项式余项的截断误差。对于底点纬度求解,本文算法与插值公式直接求解法[7]相比,省去了复杂数学公式推导和精度估计,更适合编程采用,同时该算法具有收敛速度快和计算精度高的特点,使得大地坐标反算结果与初始值符合性很好。
| [1] |
孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2007.
|
| [2] |
刘仁钊, 伍吉仓. 任意精度的子午线弧长递归计算[J]. 大地测量与地球动力学, 2007, 27(5): 59-62. |
| [3] |
殷海峰, 白征东, 程伯辉. 高斯投影公式的机助推导[J]. 测绘科学, 2008(2): 7-9. |
| [4] |
刘修善. 计算子午线弧长的数值积分法[J]. 测绘通报, 2006(5): 4-6. |
| [5] |
杨建华, 杨志强, 王腾军. 高斯投影反算中求底点纬度值的牛顿迭代法[J]. 西安科技大学学报, 2005(1): 57-59. |
| [6] |
赵长胜. 高斯投影坐标反算的迭代算法[J]. 测绘通报, 2004(3): 16-17. |
| [7] |
郑彤, 边少锋. 子午线弧长反问题新解[J]. 武汉大学学报·信息科学版, 2007, 32(3): 255-258. |
| [8] |
过家春, 赵秀侠, 徐丽, 等. 基于第二类椭圆积分的子午线弧长公式变换及解算[J]. 大地测量与地球动力学, 2011, 31(4): 94-98. |
| [9] |
过家春, 李厚朴, 庄云玲, 等. 依不同纬度变量的子午线弧长正反解公式的级数展开[J]. 测绘学报, 2016, 45(5): 560-565. |
| [10] |
过家春. 子午线弧长公式的简化及其泰勒级数解释[J]. 测绘学报, 2014, 43(2): 125-130. |
| [11] |
王继刚, 崔旭升, 张成, 等. 计算子午线弧长的常微分方程数值法[J]. 测绘通报, 2012(9): 1-3. |
| [12] |
杨丽坤, 雷伟伟. 计算子午线弧长与底点纬度的常微分方程数值解法[J]. 测绘科学技术学报, 2017, 34(6): 560-563. |
| [13] |
康世英. 基于国家坐标系的独立坐标系建立新方法[J]. 测绘地理信息, 2018, 43(15): 58-60. |
| [14] |
李泽球. 底点纬度的一种便捷算法[J]. 测绘通报, 2014(3): 122-123. |
| [15] |
李庆阳, 王能超, 易大义. 数值分析:第4版[M]. 北京: 清华大学出版社, 2001.
|
| [16] |
李文彬, 翟高鹏, 花向红, 等. 基于Romberg积分的线路中线测设统一坐标模型算法实现[J]. 测绘工程, 2014, 23(6): 27-30. |
 2020, Vol. 45
2020, Vol. 45

