| 基于深度图像的建筑物点云平面边界线提取算法 |
2. 武汉大学灾害监测与防治研究中心,湖北 武汉,430079;
3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉,430079
2. Disaster Monitoring and Prevention Research Center of Wuhan University, Wuhan 430079, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
三维激光扫描技术是获取建筑物空间数据的重要手段之一。在建筑物立面测量中,准确提取建筑物的平面特征是必要的。目前,国内外有很多学者对点云数据的边界特征识别进行了研究,主要采用曲率极值和梯度分割法识别边界点。文献[1, 2]采用局部坐标系内的二次多项式曲面来逼近点云,通过估算曲面极值点提取出边界点,这种方法需要计算每一个数据点的曲率值,其计算过程非常复杂,得出的曲率值也受到其估计方法的直接影响,有时可能和真实的曲率差别较大,而且该方法对噪声数据非常敏感。孙殿柱等[3]运用R*-tree动态空间索引结构组织,基于该结构获取采样点的k个近邻点作为局部曲面参考数据,以最小二乘法拟合该数据的微切平面,并将采样点和k个近邻点向微切平面投影,根据采样点与其k个近邻点所对应投影点连线的最大夹角识别散乱点云边界特征。但该算法需要提取点的k近邻点及进行夹角的计算,其计算量也不小,同时,R*-tree的创建非常复杂,使得算法的时间复杂度增强。谢建春等[4]计算点云剖面上的坡度值梯度,设置梯度阈值提取出特征点和坡坎,该方法具有一定的抗噪能力,但是无法排除连续树冠上的噪声点。
近些年,国内外利用深度图像进行点云边界提取形成了热潮。Li等[5]提出基于降维的点云分割算法,将点云数据转化为类似灰度图的二维数据,然后利用数字图像处理技术提取边界;Sirmacek等[6]提出了一种从激光扫描点云数据中自动分类树木的方法,首先将点云数据投影到地面,点云数据z坐标与地面的z坐标之差作为深度值生成深度图像,将树木与其他地物分离;Jakovljevic等[7]提出一种利用小波变换针对点云深度数据进行平面数据分割的新方法,但是该方法对噪声十分敏感;胡鑫等[8]提出了一种基于图像法的点云数据边界特征的自动提取方法,采用图像处理中梯度求解方法,对点云中每一点处的法矢和曲率进行估计,通过阈值得到候选边界点,进一步拟合边界曲线;孙晓兰等[9]将三维点云坐标数据转化成2.5维深度图像,分析并评估了扫描线迭代法、双方向曲率法、二阶微分算子法等3种算法在深度图像边缘检测中的性能。但是目前深度图像生成过程格网分辨率大小的设置严重影响了得到的深度信息,此外,边缘检测算子对观测噪声非常敏感,这些问题制约了利用深度图像处理点云数据的发展。针对以上问题,本文以地面三维激光扫描建筑物数据为对象,提出一种快速提取建筑物点云数据边界线的算法。
1 建筑物点云平面边界提取算法基于深度图像的建筑物点云平面边界线提取算法的基本思想是:将点云坐标数据先进行目标分割,其目的是为了从含有噪声和遮挡的原始点云数据中分割出建筑物墙体及附属物表面;然后转化为二维的深度图像, 包括参考基准面建立和深度值内插;最后,探测深度图像的边界,利用深度值与点云坐标的对应关系提取建筑物点云边界线。
1.1 目标分割三维激光扫描获得海量数据,其中不仅包含需要的建筑物信息,还包含其他信息如地面点和遮挡,这些数据不仅影响数据处理速度,还严重影响了特征提取效果。因此有必要对点云进行分割,提取出目标点云。本文按照点云到建筑物墙面的距离进行多阈值分割,首先选取在建筑物墙面上的点云数据,按照正交整体最小二乘方法[10]求出墙面平面方程和法向量。
| $a\left( {\bar x} \right) + b\left( {\bar y} \right) + c\left( {\bar z} \right) = 0 $ | (1) |
式中,a、b、c为拟合平面待求参数;
各点到拟合平面的距离平方和为:
| $ \begin{array}{l} D\left( {a, b, c, \bar x, \bar y, \bar z} \right) = \\ \sum\limits_{i = 1}^n {\frac{{{{\left[{a\left( {{x_i}-\bar x} \right) + b\left( {{y_i}-\bar y} \right) + c\left( {{z_i}-\bar z} \right)} \right]}^2}}}{{{a^2} + {b^2} + {c^2}}}} \end{array} $ | (2) |
总体最小二乘拟合考虑使D(a, b, c, x, y, z) 最小化。设矩阵
然后,计算点云数据集到拟合平面的距离di:
| $ {d_i} = \frac{{|a\left( {{x_i}-\bar x} \right) + b\left( {{y_i}-\bar y} \right) + c\left( {{z_i}-\bar z} \right)|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }} $ | (3) |
根据di直方图和建筑物像片,依据不同物体阈值δ对点云进行分割,分别得到建筑物墙体、附属物表面数据和其他噪声数据。
1.2 深度图像生成地面三维激光扫描系统坐标系是以扫描仪为中心的独立坐标系,所以得到的建筑物立面点云数据的法向量指向可以是任意的,需要先将分割后的建筑物数据进行旋转,满足建筑物平面平行于XOY面,Z值表示点到XOY面的距离。然后,将旋转后的点云数据根据其空间分布特征 (平面距离、Z值差异、点密集程度等) 进行平面投影,形成二维的深度图像。
根据平面拟合得到的法向量和旋转后的法向量nz=(0, 0, -1) 求出旋转矩阵Rw(θ),解算流程为:
1) 根据n和nz=(0, 0, -1),求出旋转角θ:
| $ \theta = {\rm{arccos}}(\frac{{\mathit{\boldsymbol{n}}\cdot{\mathit{\boldsymbol{n}}_z}}}{{\mathit{\boldsymbol{|n|}}\cdot|{\mathit{\boldsymbol{n}}_z}|}}) $ | (4) |
由n和nz叉乘求出单位旋转轴:
| $ \mathit{\boldsymbol{\omega}} = \frac{{\left( {{\mathit{\boldsymbol{n}}_z} \times \mathit{\boldsymbol{n}}} \right)}}{{|({\mathit{\boldsymbol{n}}_z} \times \mathit{\boldsymbol{n}})|}} $ | (5) |
2) 按照罗德里格旋转公式求出绕轴ω旋转的矩阵Rω(θ):
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{\omega }}\left( \theta \right) = }}\\ \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\theta + \omega _{_x}^{^2}(1-{\rm{cos}}\theta )} & {{\omega _x}{\omega _y}(1-{\rm{cos}}\theta )-{\omega _z}{\rm{sin}}\theta } & {{\omega _y}{\rm{sin}}\theta + {\omega _x}{\omega _z}(1 - {\rm{cos}}\theta )}\\ {{\omega _z}{\rm{sin}}\theta + {\omega _x}{\omega _z}(1 - {\rm{cos}}\theta )} & {{\rm{cos}}\theta + \omega _{_y}^{^2}(1 - {\rm{cos}}\theta )} & { - {\omega _x}sin\theta + {\omega _y}{\omega _z}(1 - {\rm{cos}}\theta )}\\ { - {\omega _y}{\rm{sin}}\theta + {\omega _x}{\omega _z}(1 - {\rm{cos}}\theta )} & {{\omega _x}{\rm{sin}}\theta + {\omega _y}{\omega _z}(1 - {\rm{cos}}\theta )} & {{\rm{cos}}\theta + \omega _{_z}^{^2}(1 - {\rm{cos}}\theta )} \end{array}} \right] \end{array} $ | (6) |
其中,ω=[ωx, ωy, ωz]。
3) 将目标点云数据乘以旋转矩阵Rω(θ),得到满足建筑物平面平行于XOY面的数据。
为了生成点云深度图像[12],首先根据扫描分辨率和Xmin、Xmax、Ymin、Ymax确定深度图像每个像元格网对应三维空间中的采样间隔dx、dy和格网的横纵坐标xxi、yyj,满足每个格网内的数据个数为1~10。
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}x = {X_{{\rm{max}}}}-{X_{{\rm{min}}}}}}{{n-1}}, \frac{{{\rm{d}}y = {Y_{{\rm{max}}}}-{Y_{{\rm{min}}}}}}{{m - 1}}\\ xx\left( i \right) = {X_{{\rm{min}}}} + \left( {i - 1} \right){\cdot}{\rm{d}}x\\ yy\left( j \right) = {Y_{{\rm{min}}}} + \left( {j - 1} \right){\cdot}{\rm{d}}y \end{array} \right. $ | (7) |
其中,i=1, 2, 3, …, n; j=1, 2, 3, …, m。
然后利用每个格网内的点云数据的Z值进行内插,确定格网像元的深度值。假设落在第 (i, j) 个格网中的激光扫描点个数为nij,格网 (i, j) 的中心点为pij0(xij0, yij0, 0),利用nij个扫描点的三维坐标加权计算格网 (i, j) 的深度值Fij。显然,每个格网的特征值受落在该格网内的扫描点的个数、空间分布形式 (即平面距离、高程差异等) 决定。扫描点距离格网中心点越远,则其权值越小;扫描点的高程值越大,则其权值越大[13]。
为了确定落在单元格 (i, j) 内每个点 (如第k个点,0<k≤nij) 的权值Wijk,将格网的特征值Fij的计算分为两个部分:第1部分由格网中所有点与格网中心点之间的XOY平面距离Dijk决定;第2部分由格网中所有点与格网中最低点之间的高程差异Hijk决定。因此对于单元格 (i, j) 内的扫描点k而言,其权值可以用式 (8) 和式 (9) 表示:
| $ \left\{ \begin{array}{l} W_{_{ijk}}^{^{XY}} = \sqrt {\frac{{{\rm{d}}{x^2} + {\rm{d}}{y^2}}}{{D_{_{ij}}^{^k}}}} \\ W_{_{ijk}}^{^{XY}} = \frac{{H_{_{ij}}^{^k}({h_{{\rm{min}}}}\left( {ij} \right)-{Z_{{\rm{min}}}})}}{{{Z_{{\rm{max}}}}-{Z_{{\rm{min}}}}}}\\ \alpha + \beta = 1.0 \end{array} \right. $ | (8) |
| $ {W_{ijk}} = \alpha {\cdot}W_{_{ijk}}^{^{XY}} + \beta {\cdot}W_{_{ijk}}^{^H} $ | (9) |
式中,W、WijkXY、WijkH分别为扫描点k与格网点中心的距离的权值以及扫描点k高程的权值;hmin (ij)、hmax (ij)分别为格网 (i, j) 中的最小高程和最大高程;Zmax、Zmin分别是整个扫描区域的最大高程和最小高程。设Zijk为格网 (i, j) 中的第k个点P(i, j, k) 的高程值,则Hijk=Zijk-Zmin。WijkXY反映了离散点与格网中心点的平面距离对格网中心点特征值的贡献;WijkH反映了格网内离散点的高程对格网中心点深度值的贡献。
根据上述定义的扫描点的权值公式,通过设定不同的值, 采用加权内插方法可以计算出格网 (i, j) 的深度值:
| $ {F_{ij}} = (\sum\limits_{k = 1}^{\sum {n_{ij}}} {{W_{ijk}}{\cdot}Z_{_{ij}}^{^k}} )/\sum\limits_{k = 1}^{{n_{ij}}} {{W_{ijk}}} $ | (10) |
最后将格网深度值Fij归化到0~255灰度空间即可得到格网对应的点云深度图像的像元值,从而得到整个扫描区域的点云深度图像。
1.3 深度图像边界探测与点云边界提取深度图像F是关于Z值的一个二维矩阵,包含深度值和NaN。NaN表示空值,即该格网内没有点云数据。格网分辨率的大小影响NaN的多少,分辨率过大,NaN很少或者没有,但是不能很好地表示细节信息;分辨率过小,很多格网内可能没有点云,NaN很多,这样就会造成扫描对象存在空洞的假象,不利于下一步提取边界,所以边界提取前需要消除虚假空洞。
深度图像边界探测的实质是找出深度值和扫描对象空洞[14]对应的NaN的分界线。在边界探测之前,首先确保F矩阵内部不存在由于分辨率设置不当形成的小区域空洞,如图 1(a)所示,即该区域格网内点云个数为0,如果存在这样的空洞,则会检测出来多余的小边界。
 |
| 图 1 深度图像小空洞填充 Figure 1 Small Holes Filling of Depth Images |
深度图像小空洞填充采取的办法是:采用4邻域连通标记NaN连通区域,即从上往下、从左向右对深度图像进行扫描,找到NaN连通区域的第一个目标段 (至少2个NaN 4邻域相连),标记该段并且压入堆栈,作为“区域增长”的种子段。检查当前段的每个像素4邻域是否有NaN并且未标记的像素,如果不存在,就把当前段弹出堆栈;如果存在,标记该段并且压入堆栈,作为新的“种子段”。后续操作不断从堆栈中取出种子段,重复上述操作,直到堆栈为空 (标记完一个NaN连通区域)。接着搜索图像中下一个未标记的NaN连通区域,重复上述操作, 直到图像中所有的NaN连通区域标记完毕。检测深度图像NaN连通区域,若NaN连通区域像素个数小于10,则认为是待填充的空洞,将该区域赋值为任意非空值。
经过上述处理,得到的深度图像为:目标物深度值和背景NaN。如图 2所示。
 |
| 图 2 深度图像 Figure 2 Depth Images |
对填充空洞后的深度图像探测边界,根据深度图像F与点云的对应关系提取点云边界。遍历深度图像,若某非空深度值F(i,j) 四邻域有一个NaN,如图 3中的①(F(i,j+1)=NaN),则以到F(i,j+1) 中心平面距离最近的点作为边界点,存储该边界点的三维坐标;若某非空深度值F(i,j) 四邻域有两个或者三个NaN,如图 3中的②、③,以到F(i,j) 中心平面距离最近的点作为边界点,存储该边界点的三维坐标;遍历深度图像矩阵,则可以得到所需要的全部边界点。
 |
| 图 3 深度图像边界像素 Figure 3 Depth Image Boundary Pixels |
此外,若非边界区域存在噪声或遮挡数据,则该区域的深度值是扫描对象和噪声的点云数据生成,深度值会受到影响,但是边界线是深度值和扫描对象空洞对应的NaN的分界线,深度值的变化并不影响边界特征。用该方法提取边界线在一定程度上减小了噪声影响。
2 实验及结果分析本文采用Riegl VZ-400三维激光扫描仪宿舍楼扫描数据验证该算法,扫描分辨率为:在50 m的距离时,点云间隔为2 cm。扫描数据如图 4所示。
 |
| 图 4 三维激光扫描建筑物点云 Figure 4 3D Laser Scanning Point Cloud of Buildings |
按照本文提出的算法,首先选取部分在墙面上的点云拟合平面。其拟合基准面为:
z=-0.158 1x+0.000 5y-14.331 0
根据式 (3) 计算点到基准面距离。画出直方图,如图 5所示。
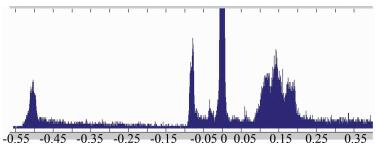 |
| 图 5 深度距离直方图 Figure 5 Histogram of Depth Distance |
由建筑物像片和分割后的数据 (图 6) 可知,-0.55~-0.45的范围表示窗户表面数据,-0.1~-0.05的范围表示墙面下水管数据,0值附近为墙面数据,di>0.1部分则是由于窗户透视引起的。于是,可设定-0.1~0.05的范围提取墙面,-0.55~-0.45的范围提取空调表面。
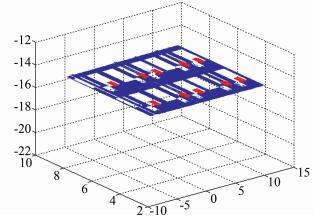 |
| 图 6 分割后数据 Figure 6 Data After Segmentation |
将建筑物墙面旋转至法向量平行于竖直方向,这样便于下一步深度图像生成时以XOY为投影面,Z为深度值。由平面法向量n=(-0.158 1, 0.000 5, -1) 及旋转后的nz=(0, 0, -1),根据式 (6) 计算的旋转矩阵为:
| $ \mathit{\boldsymbol{R = }}\left[{\begin{array}{*{20}{c}} {0.9877} & 0 & {0.1562}\\ 0 & {1.0000} & {-0.005}\\ {-0.1562} & {0.005} & {0.9877} \end{array}} \right] $ |
根据点云扫描分辨率,如图 7所示,设定深度图像格网分辨率为0.025 m×0.03 m。
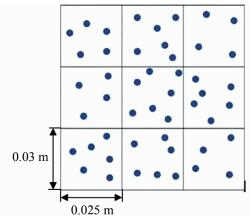 |
| 图 7 格网内点云密度示意图 Figure 7 Sketch Map of Point Cloud Density Inside Grids |
由式 (8)、式 (9)、式 (10) 得到墙面和空调的深度图像,如图 8所示。由图 8放大细节图可知,为了兼顾细节信息,深度图像内部存在小区域空洞,对其进行空洞填充后的结果如图 9所示。对墙面和空调表面分别提取边界线,得到的建筑物点云边界如图 10所示。
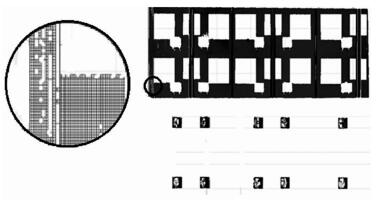 |
| 图 8 建筑物深度图像 Figure 8 Depth Images of Buildings |
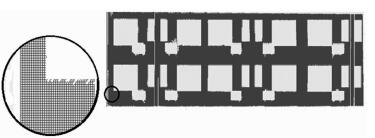 |
| 图 9 空洞填充后的建筑物深度图像 Figure 9 Depth Images of Buildings After Holes Filling |
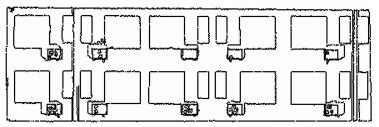 |
| 图 10 建筑物点云边界线 Figure 10 Boundary of Building Point Cloud |
为了更加直观地验证边界提取效果,将边界线与分割后的点云共同显示,点云以灰色表示,墙面边界和空调边界线以黑色表示,如图 11所示表明在存在空洞的情况下边界线较好地吻合建筑物边界。
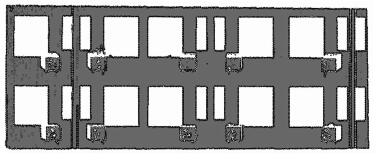 |
| 图 11 边界线与分割后点云 Figure 11 Boundary and Point Cloud After Segmentation |
3 结束语
本文以建筑物三维激光扫描数据为研究对象,提出一种基于深度图像的建筑物点云数据边界线提取的方法。该方法充分借鉴了图像处理的一些方法,克服了分辨率对深度图像生成的影响,而且边界提取不受非边缘处噪声影响,能够较好地实现建筑物边界线的快速提取。
| [1] | Milroy M J, Bradley C, Vickers G W. Segmentation of a Wrap-around Model Using an Active Contour[J]. Computer Aided Design, 1997, 29(4): 299–320 DOI: 10.1016/S0010-4485(96)00058-9 |
| [2] | Yang M, Lee E. Segmentation of Measured Point Data Using a Parametric Quadric Surface Approximation[J]. Computer Aided Design, 1999, 31(7): 449–457 DOI: 10.1016/S0010-4485(99)00042-1 |
| [3] | 孙殿柱, 范志先, 李延瑞. 散乱数据点云边界特征自动提取算法[J]. 华中科技大学学报 (自然科学版), 2008, 36(8): 82–84 |
| [4] | 谢建春, 姚吉利, 马宁, 等. 基于坡度梯度的点云数据中坡坎探测方法研究[J]. 测绘地理信息, 2015, 40(6): 53–56 |
| [5] | Li M, Hao Q, Song Y, et al. New Algorithms Based on Data Reorganization for 3D Point Cloud Data Partition[J]. Journal of Gastroenterology & Hepatology, 2012, 8558(1): 85580s–85580s-7 |
| [6] | Sirmacek B, Lindenbergh R C. Automatic Classification of Trees from Laser Scanning Point Clouds[C].International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, La Grande Motte, France, 2015 |
| [7] | Jakovljevic Z, Puzovic R, Pajic M. Recognition of Planar Segments in Point Cloud Based on Wavelet Transform[J]. Industrial Informatics, IEEE Transactions on, 2015, 11(2): 342–352 |
| [8] | 胡鑫, 习俊通, 金烨. 基于图像法的点云数据边界自动提取[J]. 上海交通大学学报, 2002, 36(8): 1118–1120 |
| [9] | 孙晓兰, 赵慧洁. 基于网格采样的深度图像表面特征提取算法[J]. 中国图象图形学报, 2007, 12(6): 1091–1097 DOI: 10.11834/jig.200706175 |
| [10] | 叶珉吕, 花向红, 陈西江, 等. 基于正交整体最小二乘平面拟合的点云数据去噪方法研究[J]. 测绘通报, 2013, (11): 37–39 |
| [11] | 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004 |
| [12] | 卢秀山, 黄磊. 基于激光扫描数据的建筑物信息格网化提取方法[J]. 武汉大学学报·信息科学版, 2007, 32(10): 852–855 |
| [13] | 魏征, 杨必胜, 李清泉. 车载激光扫描点云中建筑物边界的快速提取[J]. 遥感学报, 2012, 16(2): 286–296 DOI: 10.11834/jrs.20120412 |
| [14] | 高红波, 王卫星. 一种二值图像连通区域标记的新算法[J]. 计算机应用, 2007, 27(11): 2776–2777 |
 2017, Vol. 42
2017, Vol. 42

