| 墙体裂缝检测中张量投票算法的应用研究 |
2. 大亚湾核电运营管理有限责任公司,广东 深圳,518108;
3. 武汉大学测绘学院,湖北 武汉,430079;
4. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Daya Bay Nuclear Power Operations and Management Co., Ltd., Shenzhen 518108, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
4. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China
目前,建筑物的健康检测成为工程研究领域中炙手可热的话题,尤其是一些具有特殊用途的建筑物,如核电站的安全壳。其中,裂缝、锈蚀等缺陷在安全壳内外表面最为常见,在核电生产中具有一定的安全隐患,及时对其进行检测并修复,可避免重大的安全事故。
早期的裂缝检测主要通过人工的方式进行,如人眼观察和利用裂缝检测仪检测[1, 2],但需要耗费大量的人力、物力和时间,还伴随着结果不精确,人无法到达的区域则无法检测等缺点。随着计算机、近景摄影测量等技术的快速普及,基于数字图像处理的裂缝检测已成为主流的方式,大量的裂缝检测算法被提出[3-10]。目前,大多数现有算法[3-7]对宽度大、对比度高、连续性好的裂缝检测效果较好,大多应用在道路裂缝和桥梁裂缝的检测。但安全壳等墙体裂缝较为细小 (最大宽度一般小于0.3 mm),对比度较低,连续性差,相似形态噪声 (如雨水冲刷过的痕迹、裂缝周边出现的剥落等) 较为严重等[11]。因此,大多数现有算法对于安全壳等细小墙体裂缝的检测并不理想。张量投票[5, 12, 13]是机器视觉和机器学习中感知重组的方法,能有效增强线性目标区域的信息,近年来被广泛应用于裂缝检测中[5, 9]。然而,现有方法在实际工程应用中易受噪声影响,精度与效率相对较低。
本文针对上述问题,结合墙体裂缝的自身特征,从精度和效率两方面对现有张量投票裂缝检测算法进行改进,创新性地提出3种改进的张量投票墙体裂缝检测算法,包括分块有选择性张量投票算法、竖向张量投票算法、轮廓膨胀过滤张量投票算法,并对提出算法进行实验验证与分析,最终得到适用于实际工程的最佳方法。
1 二阶张量投票本文以二阶张量对二维空间中的几何数据进行描述,运用投票关联法则,以矢量叠加的方式实现空间数据和信息之间的相互传递与关联,并通过二阶张量与二阶矩阵之间的相似性,利用矩阵的特征值与特征向量进行分析、表达,以增强墙体裂缝目标信息。二阶张量投票算法具体可分为张量编码、张量计算和特征分析。
1.1 张量编码假设I(x, y) 表示一幅二值影像,当二值影像中 (x, y) 位置处的像素值为0时,则将此点的信息用二阶张量表示为
张量计算是指通过投票的方法将某点的张量场强信息传递给该点邻域中的其他各点,通过场强信息累加,突出墙体裂缝目标信息。投票前需要计算投票域,包括棒型和球型投票域,如图 1所示。
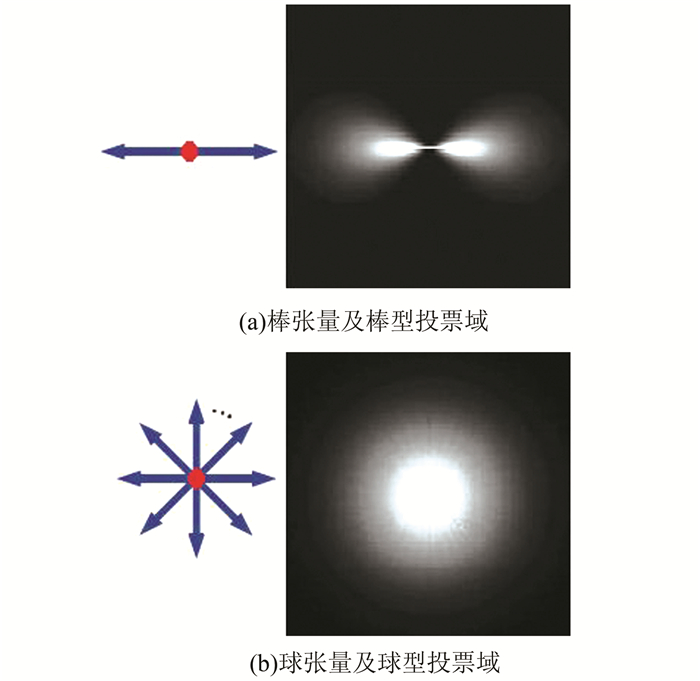 |
| 图 1 棒型域和球型域示意图 Figure 1 Diagram of the Stick Field and Ball Field |
首先,计算棒型投票域,并基于棒型投票域结果计算得到球型投票域。棒型投票域中每点投票值的计算公式为:
| $ {\boldsymbol{V}_1} = D\cdot{{\boldsymbol N}^{\rm{T}}} $ | (1) |
式中,V 1为投票值;N T表示两点之间的梯度向量;D为投票域的核函数,也称为显著性衰减函数,表示为:
| $ D = {{\rm{e}}^{ - {\rm{ }}\frac{{{s^2} + c{k^2}}}{{{\sigma ^2}}}}} $ | (2) |
式中,s表示两点之间的弧长;k表示连接两点间弧线的曲率;c=-16·log0.1(σ-1)/π2用来控制函数随着曲率的退化速度;σ表示投票的尺度,是控制投票域范围的关键因素。
球型投票域,其投票场值绕投票域的中心点间隔一定的角度θ进行旋转,本文中取旋转角度为π/16,表示为:
| $ {\boldsymbol{V}_2} = \frac{1}{{32}}\int_0^{2{\rm{\pi }}} {{\boldsymbol{V}_1}} {\rm{d}}\theta $ | (3) |
得到棒型和球型投票域后,进行投票计算,首先进行球型投票,然后进行棒型投票。具体投票过程如图 2所示,P1点接受来自邻域范围内的其他点的球型投票值,例如,图中的O点对其投票,将收集到的投票值进行累加得到投票结果R,对R进行特征分析得到初始方向和表示初始线性显著度因子的特征值;将分析结果赋予棒型投票,按照上述投票规则得到棒型投票累加结果,对结果进行特征分析,得到P2点的裂缝出现概率;最后,依次对其他点 (如图中P2点) 按照上述过程进行张量投票的计算,可有效检测墙体裂缝目标信息。
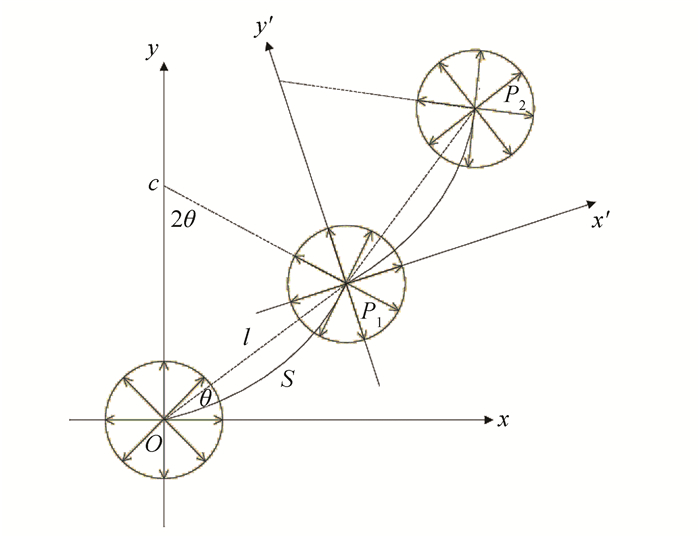 |
| 图 2 投票过程示意图 Figure 2 Diagram of the Voting Progress |
1.3 特征分析
将得到的张量计算结果R进行分解为:
| $ \begin{array}{*{20}{l}} {{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{{\overrightarrow \alpha }_1}}&{{{\overrightarrow \alpha }_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0\\ 0&{{\lambda _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\overrightarrow \alpha _1^{\rm{T}}}\\ {\overrightarrow \alpha _2^{\rm{T}}} \end{array}} \right] = }\\ {\;\;\;\;\;\;{\lambda _1}{{\overrightarrow \alpha }_1}\overrightarrow \alpha _1^{\rm{T}} + {\lambda _2}{{\overrightarrow \alpha }_2}\overrightarrow \alpha _2^{\rm{T}} = }\\ {\left( {{\lambda _1} - {\lambda _2}} \right){{\overrightarrow \alpha }_1}\overrightarrow \alpha _1^{\rm{T}} + {\lambda _2}({{\overrightarrow \alpha }_1}\overrightarrow \alpha _1^{\rm{T}} + {{\overrightarrow \alpha }_2}\overrightarrow \alpha _2^{\rm{T}})} \end{array} $ | (4) |
式中,α1、α2表示法向和切向;λ1、λ2表示法向和切向对应的大小;λ1-λ2是表征线性的显著度的量。通过所有点的特征分析将会得到一幅表征裂缝出现在某个位置可能性的概率图。若λ1-λ2 > 0,且λ1-λ2的数值越大,则表示该点位于裂缝的可能性越大,这对于墙体裂缝目标信息的增强起到了至关重要的作用。
2 改进的张量投票算法原始张量投票算法对于增强线性目标的强度起到了很好的作用,但其易受噪声影响,精度和效率较低,不利于实际工程应用。为了使算法更好地应用于工程领域,本文在原始二阶张量投票算法的基础上提出3种改进的张量投票算法,包括分块有选择性张量投票算法、竖向张量投票算法、轮廓膨胀过滤张量投票算法。
2.1 分块有选择性张量投票分块有选择性张量投票的核心思想是:墙体裂缝的发展趋势具有单一性特点,一条裂缝往往不可能遍布整张影像范围,因此,将一幅较大的影像分割成若干个小区域,对分块的小区域影像进行筛选排查,以避开对非目标区域投票的过程,从而更高效地检测裂缝目标。
如何有效地判别裂缝区域是本算法的关键。仔细观察有裂缝的二值化影像和无裂缝的二值化影像,可以明显发现如下两条规律:① 裂缝区域的二值影像,即使在有噪声干扰的情况下,连在一起的点群最大长度也大于一定的范围,无论裂缝的断裂情况有多么的严重,这样的统计规律都存在;② 裂缝区域中包含非零像素点的点群密度要大于其他地方的点群密度。利用以上两特性对分块区域进行排查,确定出包含裂缝信息的可疑区域,仅对可疑区域进行张量投票分析,从而高效地对墙体裂缝进行检测。
2.2 竖向张量投票利用原始二阶张量投票算法对墙体裂缝目标进行检测时,需经两步投票计算过程:① 进行球型投票,将结果进行特征分析,得到初始张量方向与场强信息;② 将①赋予到棒型场进行棒型投票的计算。执行上述两步投票的过程需耗费大量的时间,对于解决工程问题很不切实际。为此,本文基于原有张量投票的思想,结合墙体裂缝本身的特征,确定投票的初始方向和初始场强加权信息,以大幅提升算法的效率。此外,根据墙体裂缝的固有特点,对投票域进行重新设计,提出新型椭球投票域,如图 3所示,利用该投票域进行投票计算,从而更有效地对裂缝目标进行增强,提高检测精度。
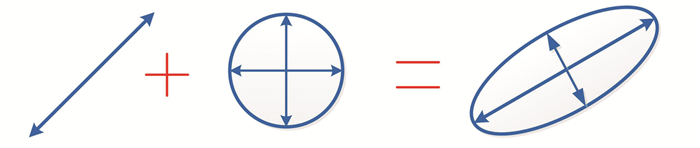 |
| 图 3 新型椭球域示意图 Figure 3 Diagram of the New Ellipsoid Field |
1) 确定投票初始方向与初始场强加权信息。对二值影像中连通的非零像素点群进行分类存储,求取每个聚类点群的最小外接矩形,得到最小外接矩形的方向信息和长度,分别作为投票初始方向和初始场强加权信息。
2) 新型椭球投票域。根据墙体裂缝特征,设计更适合于裂缝检测的新型椭球投票域。提出的新型椭球投票域是棒型域和球型域的结合,基本思路为:对球型投票域进行拉伸,拉伸的程度需要经过试验综合评定,本文沿水平方向拉伸1.5倍的范围,然后根据1) 中确定的初始投票方向,将椭球域的长轴绕着投票域中心进行旋转,得到最终的椭球投票域。
2.3 轮廓膨胀过滤张量投票算法考虑到墙体裂缝影像的复杂背景以及裂缝断裂不连续的特征,本文提出改进的轮廓膨胀过滤张量投票算法。本算法的关键在于设计有效的卷积核进行轮廓膨胀,以及对轮廓膨胀后的裂缝影像进行噪声的过滤去除。
1) 轮廓膨胀。在形态学领域中,膨胀操作是指将影像或者影像中一部分连在一起的区域范围进行扩大操作,目的是形成完整的或者更大的连通区域。
轮廓膨胀示意如图 4所示,其中,A为目标信息,B为膨胀操作的卷积核。本文根据墙体裂缝的形态等相关信息,设计有针对性的带有方向信息的新型卷积核,如图 5所示,利用该卷积核对目标信息进行膨胀操作,可更有效地对墙体裂缝目标进行增强。
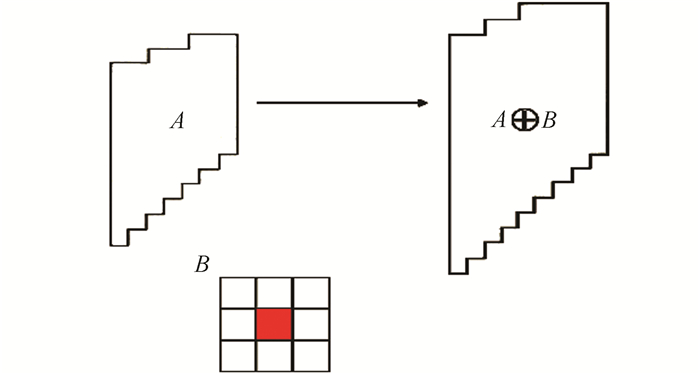 |
| 图 4 轮廓膨胀示意图 Figure 4 Diagram of the Contour Expansion |
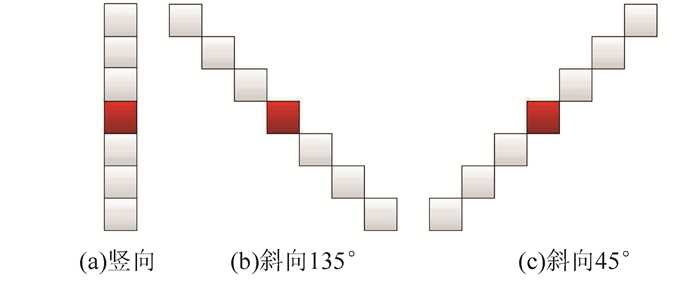 |
| 图 5 带有方向信息的卷积核 Figure 5 Convolution Kernel with Direction |
2) 过滤准则。对二值裂缝影像进行膨胀操作后,线性目标在增强的同时,噪声被一起增强,因此, 需要建立一定的过滤准则对噪声进行滤除。本文根据墙体裂缝特点,选取以下3个过滤准则:① 轮廓外接矩形长度大于一定范围的目标信息;② 轮廓外接矩形长宽比大于一定范围的目标信息;③ 形心比小于一定范围的目标信息。
形心比是一种适用于线性目标识别的评价因子,为Yamaguchi等[10]提出,形心比的值越趋于0,表示目标信息为线性目标的可能性越大。
3 实验结果与分析本文以实际工程应用中某核电站安全壳的外壁墙体裂缝影像为实验数据,对3种改进算法——分块有选择性张量投票算法、竖向张量投票算法、轮廓膨胀过滤张量投票算法进行验证,并与原始张量投票检测算法[11]以及添加线性加权因子的张量投票裂缝检测算法[9]进行对比分析。实验数据为实地采集的2 000像素×2 000像素大小的安全壳外壁真实二值影像,如图 6所示。在影像采集中,所采用的相机型号为尼康D800,配备尼康AF 28 mm f/2.8D定焦广角镜头。为了更全面地对算法进行验证,选用尺度因子参数σ1=15, σ2=25进行实验,记录各方法在不同情况下的运行时间,如表 1所示,对应的运行裂缝检测效果如图 7所示。
 |
| 图 6 原始二值影像 Figure 6 Original Binary Image |
| 表 1 各算法运行时间表/s Table 1 Running Time of Different Algorithms/s |
 |
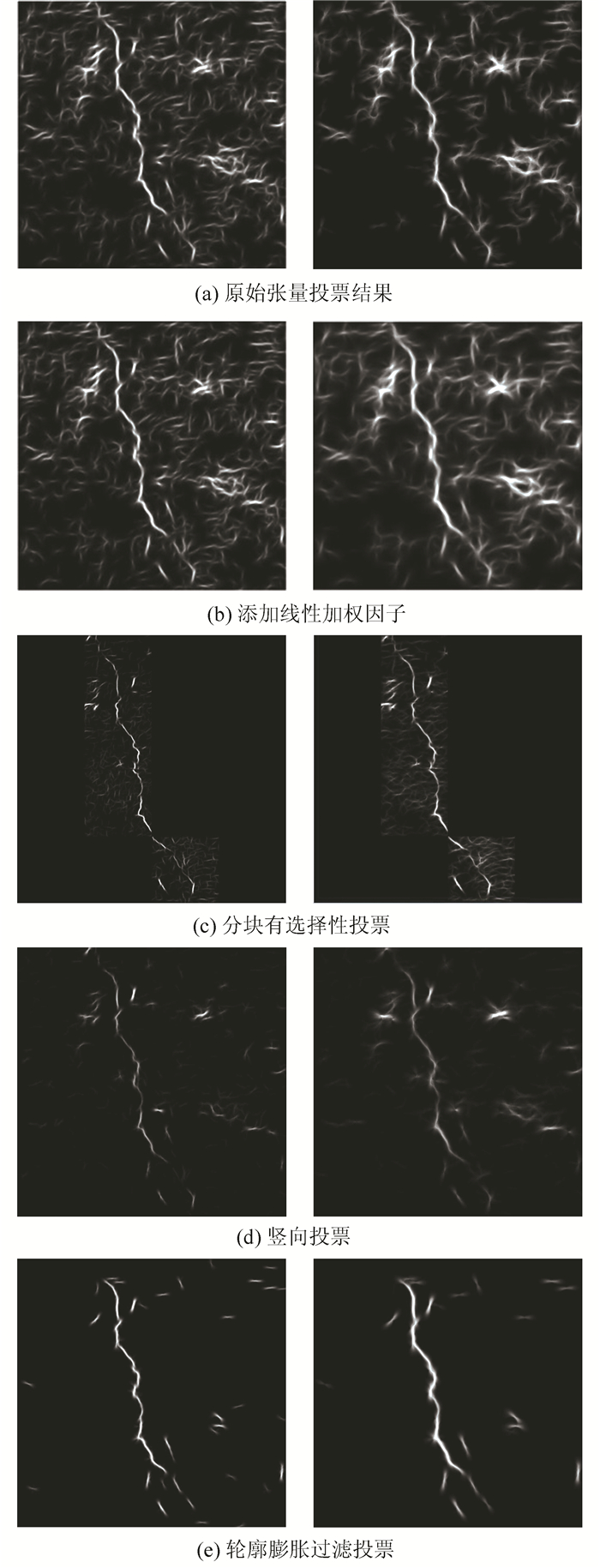 |
| 图 7 各算法不同尺度因子裂缝检测结果图 Figure 7 Crack Detection Results of the Different Algorithms with Different Scale Factors |
实验结果表明,原始张量投票算法和添加线性加权因子的张量投票裂缝检测算法对噪声较为敏感,检测结果受噪声影响较为严重。而本文提出的3种改进算法在增强墙体裂缝目标的同时,可有效削弱周边离散噪声点群的影响,得到较为理想的检测结果。同时,改进算法对参数鲁棒性高,运行稳定。相比而言,轮廓膨胀过滤张量投票算法对墙体裂缝目标的增强最为突出,噪声剔除也较为明显,检测效果最好。从表 1可以发现,本文提出的3种改进算法的运行效率均得到大幅提升,其中轮廓膨胀算法耗时最少,平均运行效率为原始张量投票裂缝检测算法的3倍,约为添加线性加权因子张量投票裂缝检测算法的10余倍。
综上所述,本文提出的3种改进张量投票墙体裂缝检测算法在检测效果和效率方面均得到较大提升,其中轮廓膨胀过滤张量投票算法相比于其他方法效果最佳。
4 结束语本文面向墙体裂缝检测,针对现有算法在实际工程应用中易受噪声影响、精度与效率较低等难题,创新性地提出3种改进的张量投票算法,包括分块有选择性张量投票算法、竖向张量投票算法、轮廓膨胀过滤张量投票算法。通过实际工程应用中某核电站安全壳壳壁的墙体裂缝检测对算法进行了实验验证。结果表明,3种改进算法均可有效抑制噪声的影响,在检测效果和效率方面均优于原始张量投票算法和现有裂缝检测方法。其中,改进的轮廓膨胀过滤张量投票墙体裂缝检测算法效果最佳,适用于解决实际工程问题。
| [1] | 刘万贵, 李维武. CRD-1裂缝检测仪简介[J]. 电力建设, 1996, (1): 63–64 |
| [2] |
王雷. 基于数字图像的混凝土结构构件裂缝测量[D]. 天津: 天津大学, 2006 |
| [3] | Abdelqader I, Abudayyeh O, Kelly M E. Analysis of Edge-Detection Techniques for Crack Identification in Bridges[J]. Journal of Computing in Civil Engineering, 2003, 17(4): 255–263 DOI: 10.1061/(ASCE)0887-3801(2003)17:4(255) |
| [4] | Chambon S, Subirats P, Dumoulin J. Introduction of a Wavelet Transform Based on 2D Matched Filter in a Markov Random Field for Fine Structure Extraction: Application on Road Crack Detection[C]. Proceedings of SPIE: The International Society for Optical Engineering, San Jose, America, 2009 |
| [5] | Guan H, Li J, Yu Y, et al. Iterative Tensor Voting for Pavement Crack Extraction Using Mobile Laser Scanning Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1 DOI: 10.1109/TGRS.2015.2401517 |
| [6] | Oliveira H, Correia P L. Automatic Road Crack Detection and Characterization[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 155–168 DOI: 10.1109/TITS.2012.2208630 |
| [7] | Salman M, Mathavan S, Kamal K, et al. Pavement Crack Detection Using the Gabor Filter[C].International IEEE Conference on Intelligent Transportation Systems, Hague, Netherlands, 2013 |
| [8] | 焦莉. 面向对象方法的路面线性裂缝识别与测量方法研究[J]. 测绘通报, 2012, (7): 27–30 |
| [9] |
邹勤. 低信噪比路面裂缝增强与提取方法研究[D]. 武汉: 武汉大学, 2012 |
| [10] | Yamaguchi T, Nakamura S, Hashimoto S. An Efficient Crack Detection Method Using Percolation-Based Image Processing[C]. IEEE Conference on Industrial Electronics and Applications, Singapore, 2008 |
| [11] | 徐亚明, 束进芳. 基于张量投票和目标追踪的墙体裂缝检测算法研究[J]. 大地测量与地球动力学, 2016, 36(4): 334–337 |
| [12] | Mordohai P, Medioni G. Tensor Voting: A Perceptual Organization Approach to Computer Vision and Machine Learning[J]. Synthesis Lectures on Image Video and Multimedia Processing, 2006, 2(1): 136 |
| [13] |
张乐飞. 遥感影像的张量表达与流形学习方法研究[D]. 武汉: 武汉大学, 2013 |
 2017, Vol. 42
2017, Vol. 42

