| ARAIM算法多故障检测排除性能初步分析 |
美国与欧盟于2004年签署了一项双边合作协议用于设计和开发新一代的民用导航定位授时系统,该项目的一个重要组成部分为确定导航系统完备性标准及相关协议。由来自联邦航空委员会、斯坦福大学、迈特公司、伊利诺伊斯理工大学、德国宇航中心、慕尼黑理工大学、欧空局、欧盟委员会、法国太空研究中心、法国国立民用航空学校和欧洲航空安全组织等机构专家组成项目小组,致力于该项目标的实现[1]。
目前,该项目小组已发布了两份关于项目的里程报告,对下一代导航系统完备性的实现方式提出了总体规划。其中,在2012年发布的第一份里程报告中就已经完整提出导航系统完备性功能的用户端高级接收机自主完好性监测(advanced receiver autonomous integrity monitoring, ARAIM)算法,并获得了令人满意的仿真结果[2]。
目前,使用实际数据对ARAIM算法进行性能验证的研究还比较少,基本上都是使用仿真数据[3]。国际上进行此项工作的有澳大利亚科廷科技大学的Ahmed E M[4]、斯坦福大学的Blanch J[5, 6]、澳大利亚新南威尔士大学的王金岭博士[7]等。国内的有武汉大学的吴云、李彬[8, 9]、中南大学的孙晓剑[10]等。以上研究工作均是建立在算法自身完全可靠基础之上的,并未考虑由于算法本身未能正确去除导航系统故障,导致导航系统性能降低的情况,本文尝试对ARAIM算法本身的检测排除性能进行评价。
1 ARAIM算法描述ARAIM算法被描述为一个递归算法[11],其核心操作是解分割过程,为方便起见,将其定义为图 1所示的固定流程ARAIM-SS。
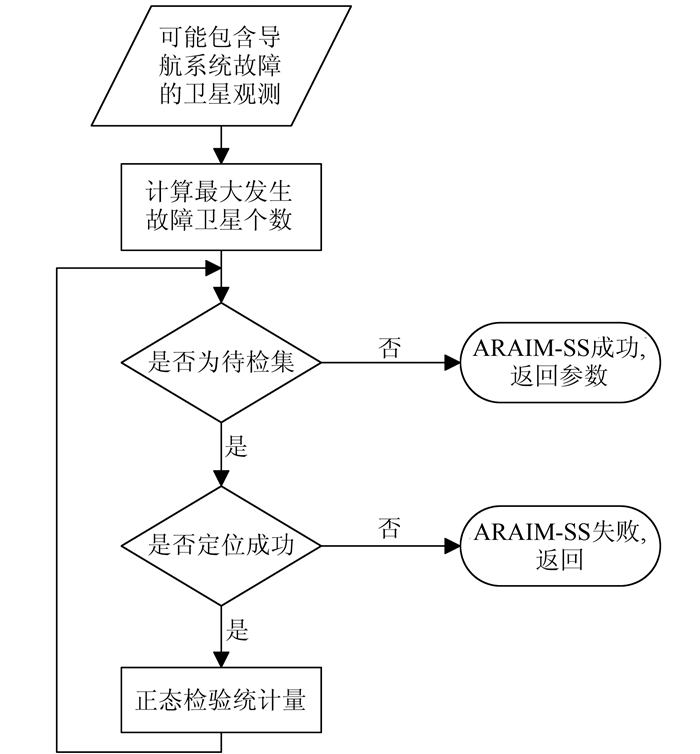 |
| 图 1 固定流程ARAIM-SS Figure 1 Fixed Process ARAIM-SS |
图 1中循环内的待检集即由总的卫星观测个数与最大故障卫星个数所确定的分割解集,ARAIM-SS通过对分割解的定位结果进行正态性检验来判断分割解集中是否存在故障卫星。在此基础之上,ARAIM算法整体如图 2所示。
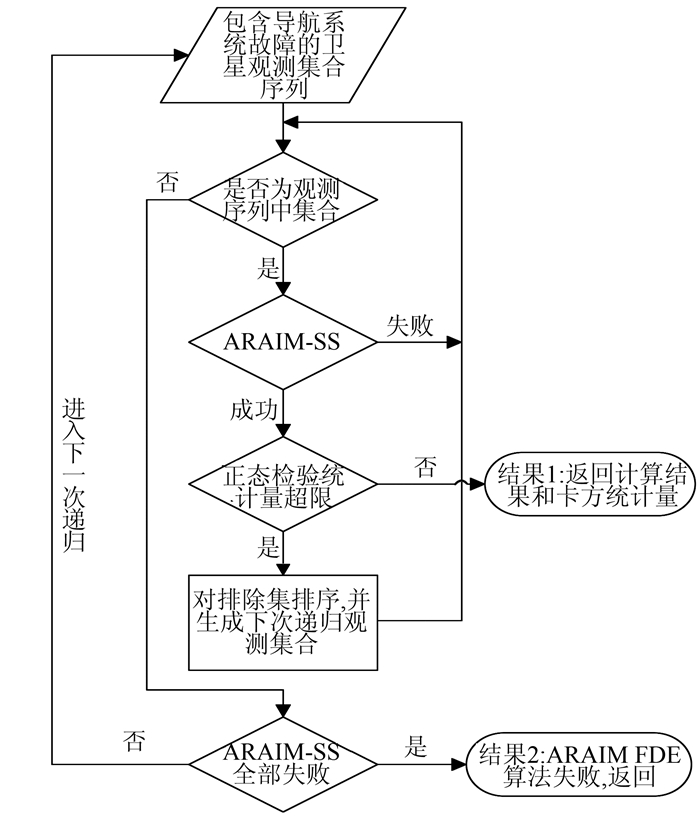 |
| 图 2 ARAIM算法总体流程 Figure 2 Overall Process of ARAIM Algorithm |
由于ARAIM算法使用递归方法,增加了计算的复杂性,因此在文献[1]中限定递归次数为2,即只对当前历元用于定位卫星观测集合以及第一次递归生成的待检观测序列进行故障检测与排除(fault detection and exclusion, FDE),若两次排除之后仍无法获得不包含导航系统故障的卫星观测集合,那么认为当前观测到的所有卫星均不可用,并对不可用卫星进行监控。
本文对ARAIM算法性能的评价涉及3个方面:①ARAIM算法成功的效率;②ARAIM算法正确检测排除卫星故障的性能;③ARAIM算法通过卡方检验的性能,通过实测数据对ARAIM算法检测排除性能进行评价。
2 ARAIM FDE算法检验结果分析 2.1 参数设置本文对2015年4月10日mor1站GPS/BD双星座数据调用ARAIM算法进行检验。参数设置如下:高度角15°,定位所用权阵中使用的用户测距精度(user range accuracy, URA)为广播星历所取值, 用户测距误差(user range error, URE)的大小根据文献[2]设置为URA的2/3,分别设置了10 m、30 m和100 m三个不同量级的粗差来表示导航系统发生故障时的情况。
2.2 ARAIM算法性能分析1) 单个卫星故障情况。图 3为由于卫星故障导致观测中出现单个10 m、30 m、100 m粗差情况下ARAIM算法对故障的检测排除能力。图中下方的3条粗直线分别表示在一天之内ARAIM算法成功历元(蓝色)、正确检验排除故障卫星历元(绿色)以及通过卡方检验历元(紫色);上方两条细线中蓝色细线为导航系统当前的垂直保护水平(vertical protect level, VPL), 红色细线为国际民航组织定义的预警值(vertical alarm level, VAL)(VPL低于VAL, 表示当前保护型水平可用)。只有在当前历元观测通过ARAIM算法检测排除导航系统故障之后,后续算法才有可能计算当前飞行器的保护水平,因此,保护型水平曲线VPL可以反映算法的检测排除效果。
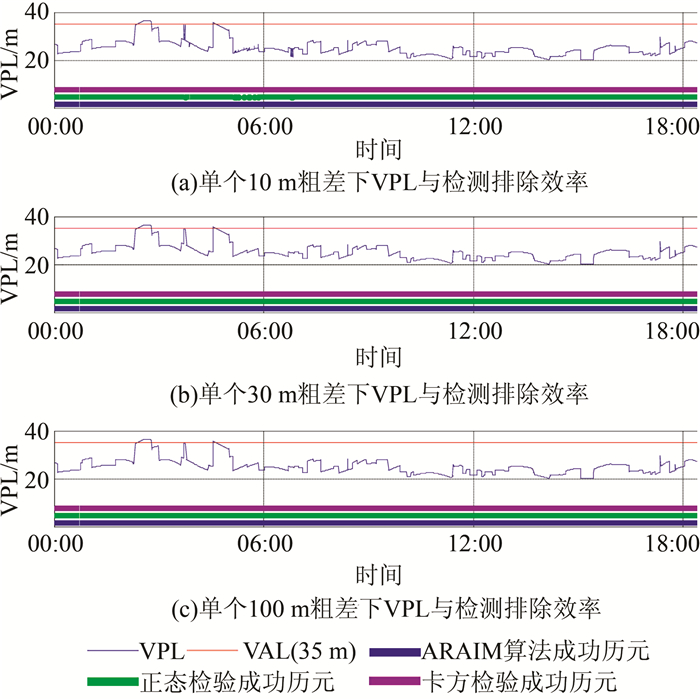 |
| 图 3 单个粗差下VPL与ARAIM算法效率 Figure 3 Algorithm Efficiency of VPL and ARAIM Under Single Fault |
对图 3进行数据统计,在一天2 880个历元之内,对于导航系统故障导致观测中出现单个10 m粗差情况, 有2 879个历元ARAIM算法成功, 有2 791个历元算法能够正确检验排除卫星故障,有2 879个历元卡方检验成功。对于导航系统故障导致观测中出现单个30 m粗差情况,有2 879个历元ARAIM算法成功, 2 879个算法检验排除卫星故障成功,有2 879个历元卡方检验成功。对于导航系统故障导致观测中出现单个100 m粗差情况, 有2 879个历元ARAIM算法成功, 2 879个历元算法成功检验排除卫星故障,有2 879个历元卡方检验成功。
2) 多(两)个卫星故障情况。图 4是对由于导航系统故障导致观测中出现两个粗差情况下ARAIM算法的一个性能展示,图中不同粗差量级下经ARAIM算法检测排除故障之后得到的保护水平VPL基本一致,与单个故障情况下经ARAIM算法得到的保护水平曲线有较显著的区别。
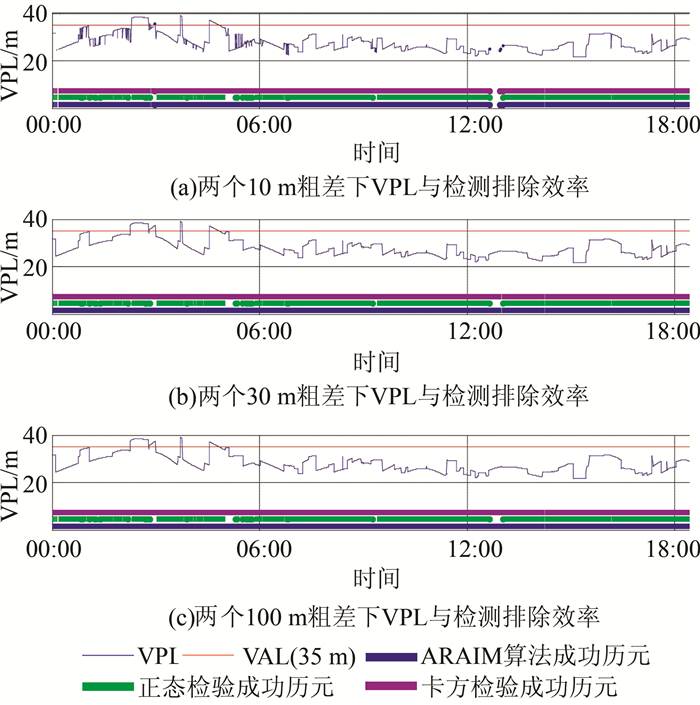 |
| 图 4 两个粗差下VPL与ARAIM算法效率 Figure 4 Algorithm Efficiency of VPL and ARAIM Under Double Faults |
对图 4进行统计,在2 880个历元内,对于导航系统故障导致观测中出现两个10 m粗差情况, 有2 819个历元ARAIM算法成功, 有2 557个历元算法能够正确检验排除卫星故障,有2 819个历元卡方检验成功。对于导航系统故障导致观测中出现两个30 m粗差情况,有2 878个历元ARAIM算法成功, 2 819个算法检验排除卫星故障成功,有2 878个历元卡方检验成功。对于导航系统故障导致观测中出现两个100 m粗差情况, 有2 879个历元ARAIM算法成功, 2 819个历元算法成功检验排除卫星故障,有2 879个历元卡方检验成功。
图 3和图 4中ARAIM算法效率统计见表 1。从表 1看出,ARAIM算法在单个卫星故障情况下表现较好,算法成功率均能达到99.97%,除了对于较小的故障导致观测粗差(10 m),故障正确检验排除效率较低(96.91%),在故障导致较为明显粗差情况下,正确检验排除故障效率也能够达到99.97%。对于卡方检验量,由于其是检验风险模型之外的导航系统故障,根据表 1可见,其与算法成功率完全一致,说明对于当天的实验数据不存在算法模型之外的导航系统故障。
| 表 1 ARAIM算法效率统计 Table 1 Efficiency Statistics of ARAIM Algorithm |
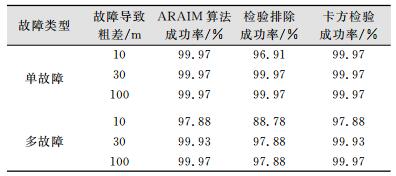 |
对比于单个故障情况下算法较为稳定的表现,从表 1可以看出,在双故障情况下,ARAIM算法不论是在成功率、正确检测排除故障效率,还是在卡方检验通过率上,均要差于单故障情况。最差的情况出现在对两个10 m粗差的检测排除效率上,只有88.78%,大大低于99.5%或者99%的可用性要求[12]。考虑到双故障出现的概率极低[2],该检测排除效率是否可以接受仍需要进一步讨论。
3 结束语本文检验了单个及多(两)个故障情形下最新的ARAIM算法检验排除性能。结果显示,ARAIM算法本身存在算法失败的概率以及不能完全检测排除出导航系统故障的概率,这会在使用算法进行完备性评价时得到一组较真实完备性性能更为保守的一组值(GEAS所给出的LPV-200/250标准)[12]。但是由于ARAIM算法失败或者不能完全检测排除导航系统故障的概率很小,在单个故障情况下,ARAIM算法的成功率能够提供99.5%的可用性产生的条件,但是在单个10 m故障的情况下,检验排除成功(漏检)的概率高于所给的参考值10-7[1];多(双)故障情况下,ARAIM算法成功率能够提供99%的可用性产生的条件(两个10 m粗差情形除外),其成功检验排除概率比单故障的情况要更低。在对导航系统完备性性能进行评价时,需要考虑到由于算法本身缺陷造成的性能损失。
| [1] | GPS-Galileo Working Group C ARAIM Technical Subgroup Interim Report, Issue 1.0[EB/OL]. (2013-09-23)[2015-12-24]. http://www.gps.gov/policy/cooperation/europe/2013/working-group-c/ |
| [2] | GPS-Galileo Working Group C ARAIM Technical Subgroup Milestone 2 Report, Issue 2.0[EB/OL]. (2015-02-11)[2015-12-24]. http://www.gps.gov/policy/cooperation/europe/2015/working-group-c/ |
| [3] | Blanch J, Walter T, Enge P. RAIM with Optimal Integrity and Continuity Allocations Under Multiple Failures[J]. IEEE Transactions on Aerospace and Electronic System, 2010, 46(3): 1 235–1 247 DOI: 10.1109/TAES.2010.5545186 |
| [4] | Ahmed E M. ARAIM for Vertical Guidance Using GPS and BeiDou[J]. Journal of Global Positioning System, 2013, 12(1): 28–37 DOI: 10.5081/jgps |
| [5] | Choi M, Blanch J, Akos D. Demonstrations of Multi-Constellation Advanced RAIM for Vertical Guidance Using GPS and GLONASS Signals[C]. The 24th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, 2011 |
| [6] | Ene A, Blanch J, Walter T, et al. Validation of Multiple Hypothesis RAIM Algorithm Using Dual-Frequency GPS and Galileo Signals[C]. Proceedings of the European Navigation Conference GNSS, Toulouse, France, 2008 |
| [7] | Hewitson S, Wang J. GNSS Receiver Autonomous Integrity Monitoring (RAIM) Performance Analysis[J]. GPS Solutions, 2006, 10(3): 155–170 DOI: 10.1007/s10291-005-0016-2 |
| [8] | Li Bin, Sang Jizhang, Wu Yun. Validation of GNSS ARAIM Algorithm Using Real Data[C]. Proceedings of CSNC, Nanjing, China, 2014 |
| [9] |
李彬. GNSS ARAIM算法的有效性研究[D]. 武汉: 武汉大学, 2013 |
| [10] | 孙晓剑, 匡翠林, 张昊楠. GPS卫星预报精密星历的SIS完备性监测方法[J]. 测绘地理信息, 2013, 38(1): 30–33 |
| [11] | Blanch J, Walter T, Enge P, et al. Advanced RAIM User Algorithm Description: Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation[C]. Proceedings of ION GNSS, Nashville, TN, 2012 |
| [12] | FAA-GEAS-Panel. Phase Ⅱ of the GNSS Evolutionary Architecture Study[EB/OL]. [2015-12-24]. http://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/gnss/library/documents/media/GEASPhaseⅡ_Final.pdf |
 2017, Vol. 42
2017, Vol. 42

