| 模拟退火法快速逼近解求模型参数 |
2. 湖南省龙山县国土资源局,湖南 龙山, 416800;
3. 中国石油天然气管道局天津设计院,天津,300457
2. Longshan Bureau of Land and Resources in Hunan Province, Longshan 416800, China;
3. China Petroleum Pipeline Bureau Tianjin Design Institute, Tianjin 300457, China
因为测绘领域大多数学模型都是非线性模型,很多观测方程都具有很强的非线性性。对于测量中大量的非线性模型,传统的方法都是进行线性近似,即将其展开为泰勒级数,取其一次项,而略去二次以上各项,如此线性近似,必然会引起模型误差。由于过去测量精度不高,线性近似引起的模型误差一般小于观测误差,故可忽略不计,随着测绘科学技术的不断发展,现在的测量技术已经大大提高,致使线性近似引起的模型误差与观测误差相当,甚至还会大于观测误差。因此,用近似的理论、模型、方法去处理很高精度的观测结果,会导致精度损失,显然是不合理的。现代科学技术要求估计结果的精度尽可能的提高。传统的线性近似的方法不能满足当今科学技术的要求,而最小二乘估计是精确解求非线性模型参数的一种有效方法,其中包括牛顿法、信赖域法、拟牛顿法、高斯-牛顿法、阻尼最小二乘法等[1]。最小二乘估计算法都需要求导计算,当函数模型比较复杂时,求导就比较困难,尤其当函数模型不可导,最小二乘算法就不能应用。模拟退火法作为一种通用概率算法,能在一个大的搜寻空间内寻找到问题的最优解,避免模型函数的求导计算,对于较复杂的不易求导的函数模型模拟退火法能有效、准确地解求模型参数。
1 模拟退火法的基本原理1953年,Metropolis等首先提出了模拟退火的思想,1983年,Kirkpatric等将SA引入组合优化领域[2],由于模拟退火法能有效解决NP难的问题,避免陷入局部最优,对初始值没有强依赖关系等,已经在很多领域得到了广泛的应用。现代的模拟退火算法形成于20世纪80年代初,其思想源于固体退火过程,及将固体加热至足够高的温度,再缓慢冷却;升温时,固体内部粒子随着温度的升高变为无序状,内能增大,而缓慢冷却时粒子又缓慢趋于有序,从理论上讲,如果冷却的过程足够缓慢,那么冷却中的任一温度时刻固体都能达到热平衡,而冷却到低温时将达到这一低温下内能的最小状态[3-8]。算法基本步骤如下:①设置一个初始温度T=T0,随机生成一个初始解xi,并计算相应的目标函数值E(x0);②令T等于冷却进度表中的下一个值Ti;③根据当前解xi进行扰动,产生一个新解xj,计算相应的目标函数值 ,得到ΔE=E(xj)-E(xi);④若ΔE <0,则新解xj被接受,作为新的当前解;若ΔE>0,则新解xj按概率exp-ΔE/Ti接受,Ti为当前温度;⑤在温度Ti下,重复Lk次的扰动和接受过程,即执行步骤③和④;⑥判断T是否已达到Tf ,如果是,则终止算法;如果否,则转到步骤②继续执行。
2 利用模拟退火法快速逼近模型参数1) 常规算法存在的问题。模拟退火法是一种通用概率算法,最优解的搜索是在定义域中反复随机进行的,在解求参数之前,无法预测参数的定义域范围,要想在一个偌大的定义域中找到精确解,具有很大的随机性,这就导致在解求模型参数时直接利用模拟退火法求解很难得到高精度解。例如,当解求一个含有3个模型参数,要求解的精度是小数点后3位时,在已确定小数点前数字的前提下,解的组合就是109个,即模拟退火法程序至少需设置109个循环,这将大大耗费求解的时间,并且很难找到精确解。
2) 本文快速逼近模型参数的方法。要利用模拟退火法达到快速求解模型参数的目的,最重要的就是尽可能缩小模拟退火法搜索的定义域范围。因此,为了克服搜索区域大的难题,可以对模型参数解进行逐级搜索,每次循环精确求解参数的一个数量级,然后再利用模拟退火法解求参数解的下一个数量级,依次逼近解的精度,当解求一个含有3个模型参数,解的精度要求是小数点后3位时,解的组合只有3×103个,大大降低了搜索的难度。利用模拟退火法进行搜索时,可以将目标函数值定义为模型拟合的残差平方和,初始值可以选择特征点代入模型解求方程组即可。
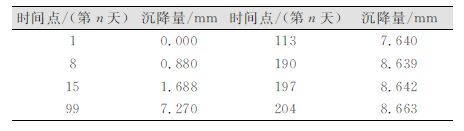
3 实例分析本文选取的数据为武咸城际铁路某个路基监测点30期的监测数据,监测数据为路基观测桩实测值,测量满足一等水准要求。数据摘录如表 1所示。
3.1 解求模型参数初始值用模拟退火法进行模型参数估计,需要尽可能缩小参数定义域的范围,以便提高搜索的效率。在进行路基沉降拟合时,双曲线拟合模型是一种比较常见的模型,其模型公式为:
| $y=t-c/a+bt-c$ | (1) |
| 表 1 某个路基监测点部分检测数据 Table 1 Part Detection Data of an Embankment Section Monitoring Point |
 |
式中,y表示拟合沉降量;t表示观测期数。对于对数模型,有3个未知参数需要求解。为了保证拟合的对数曲线反映出真实的沉降变形,可分别取观测前期、中期和后期的观测数据,以控制拟合曲线的走向与实际变形沉降曲线相一致,得出3个方程组,解方程组即可得出模型参数的初始值,这可以用MATLAB轻松实现。
为获取a、b、c大致的取值范围以确定模拟退火法的搜索区间,随机抽出两组观测值计算得出模型参数的初始值如表 2所示。其中,第一组是第8天、第99天和第197天的观测数据;第二组是第15天、第113天和第190天的观测数据。
| 表 2 模型的初始值计算结果 Table 2 Initial Values of the Model |
 |
3.2 逐级逼近参数精确值
由表 2可知,通过解方程组,仅通过3个观测数据就可以确定模型参数的大致区间,而不是运用最小二乘原理将所有观测数据综合考虑得出的最优解。解方程组能确定参数的位数级,虽不能精确确定参数第一位数的确切值,但可以确定模拟退火法的初始搜索范围。因为位数级已经确定,第一位数的实际取值只需在一个小的范围内进行搜索,模拟退火法很容易就能完成,如本例中,通过随机选择的两组数据解方程组得出的a、b、c值,即可确定模拟退火法的搜索范围,结合表 2可知,可利用模拟退火法在0~10之间搜索a的取值,在0~0.15之间搜索b的取值,在0~10之间搜索c的取值。确定参数a、b、c的第一位非零数字,组合为1.5×103个,对于计算机利用模拟退火法进行搜索,花费的时间几乎可以忽略。求得第一位非零数字以后,后几位的数字则可以继续依次逐级逼近。
通过第一步搜索得出参数的小数点后一位后,再将得出的参数值作为初始值确定参数的小数点后第二位,最后求小数点后第三位。模拟退火法解求参数的每一次逼近结果如表 3所示。
| 表 3 模拟退火法逐步逼近解求参数结果 Table 3 Simulated Annealing Method Successive Approaching to Obtain Parameters Results |
 |
由表 3可知,虽然模拟退火法理论上永远达不到最小二乘法解求模型参数的精度,但是可以无限逼近其解求精度。
为了验证双曲线模型在本例沉降预测中的可靠性,本文采用了另外一种常用的路基沉降预测法——灰色法来进行对照。两种预测方法的拟合结果以及拟合残差分别如图 1和图 2所示。图 1为咸城际路基下沉量拟合-实测曲线,图 2为武咸城际路基沉降拟合残差。
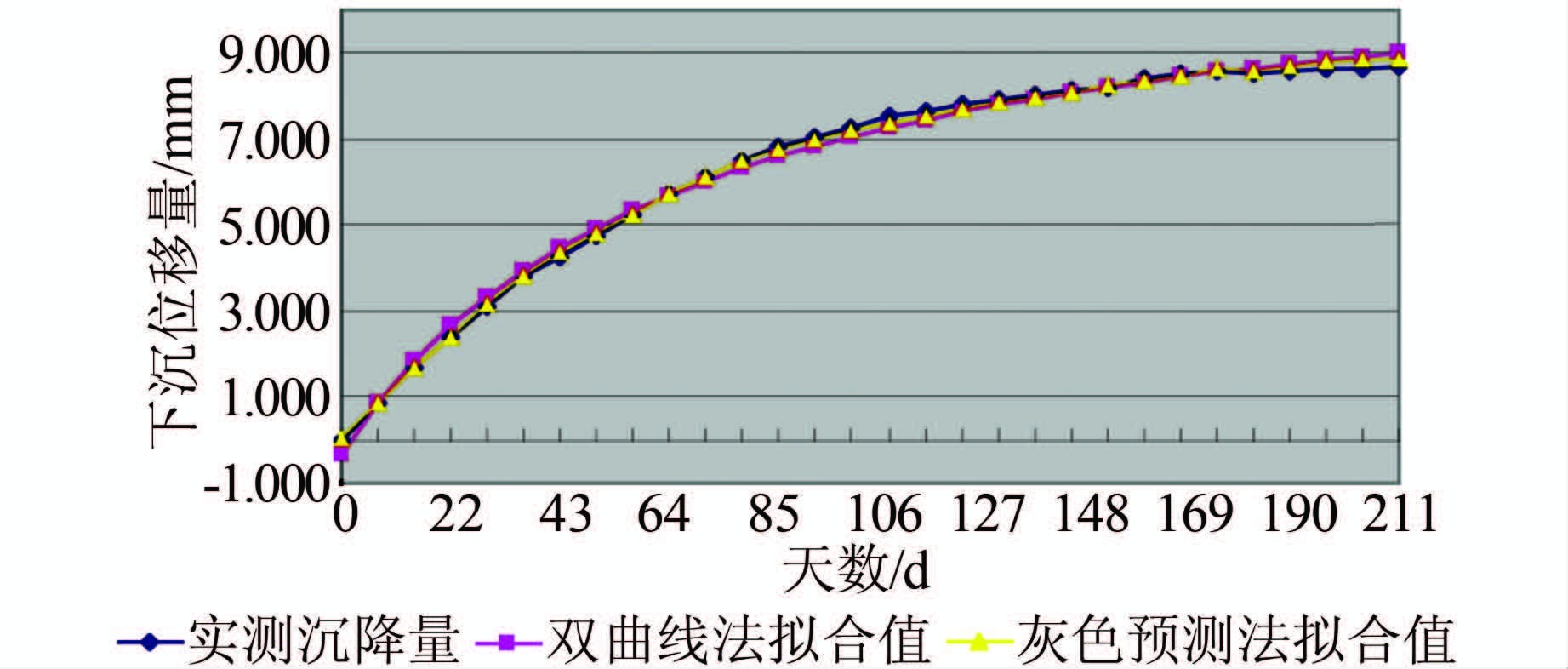 |
| 图 1 逐级求解后的双曲线及灰色预测法拟合结果 Figure 1 Fitting Results of Hyperbolic Curve and Grey Prediction Methods After Progresively Solution |
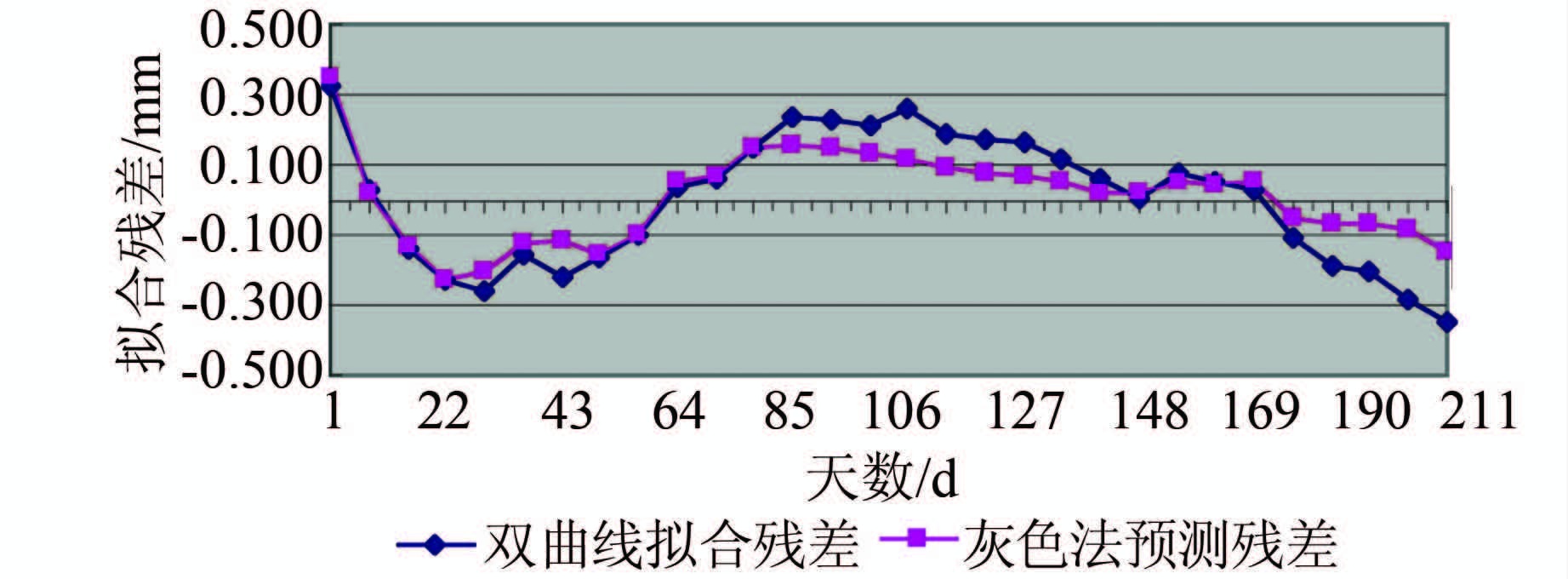 |
| 图 2 双曲线法及灰色预测法拟合残差图 Figure 2 Fitting Residual Plots of Hyperbolic Cruve and Grey Prediction Methods |
由图 1、图 2可知,在本例中,双曲线法和灰色预测法拟合的结果一致,证明了本文提出的用模拟退火法逐级解求的双曲线参数是有效的。
4 结束语本文提出了利用模拟退火法快速解求模型参数的方法,对双曲线法和灰色预测法的精度可不深究。利用模拟退火法逐级逼近进行模型参数估计,能很大程度上降低模拟退火法搜索参数的定义域范围,从而提高了搜索的效率。模拟退火法无需对函数模型方程进行求导计算,避免了复杂函数求导难的问题。对于某些求导难的函数模型,模拟退火法无疑是一种较好的模型参数估计的途径。
| [1] |
王新洲.
非线性模型参数估计理论与应用[M]. 武汉: 武汉大学出版社, 2002 .
Wang Xinzhou. Theory and Application of Parameter Estimation for Nonlinear Mode[M]. Wuhan: Wuhan University Press, 2002 . |
| [2] |
史峰, 王小川, 郁磊, 等.
MATLAB神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社, 2010 .
Shi Feng, Wang Xiaochuan, Yu Lei, et al. Analysis of 30 Cases of MATLAB Neural Network[M]. Beijing: Beihang University Press, 2010 . |
| [3] |
周品, 何正风.
MATLAB数值分析[M]. 北京: 机械工业出版社, 2009 .
Zhou Pin, He Zhengfeng. MATLAB Numerical Analysis[M]. Beijing: China Machine Press, 2009 . |
| [4] |
卓金武, 魏永生, 秦健, 等.
MATLAB在数学建模中的应用[M]. 北京: 北京航空航天大学出版社, 2011 .
Zhuo Jinwu, Wei Yongsheng, Qin Jian, et al. Application of MATLAB in Mathematical Modeling[M]. Beijing: Beihang University Press, 2011 . |
| [5] |
黄声享, 尹晖, 蒋征, 等.
变形监测数据处理. 武汉.武汉大学出版社[M]. 2003 .
Huang Shengxiang, Yin Hui, Jiang Zheng, et al. Deformation Monitoring Data Processing[M]. Wuhan: Wuhan University Press, 2003 . |
| [6] |
杨发群, 邱卫宁, 王俊丰, 等. Excel规划求解在桥墩沉降趋势分析中的应用[J].
测绘地理信息,2012,37(6) : 20–22.
Yang Faqun, Qiu Weining, Wang Junfeng, et al. Application of Excel Solver in the Bridge Pier Subsidence Trend Analysis[J]. Journal of Geomatics,2012,37(6) : 20–22. |
| [7] |
刘建军, 陈明峰, 叶子飘. 阻尼最小二乘法与模拟退火法结合实现非线性模型参数的估计[J].
井冈山大学学报(自然科学版),2010,31(6) : 10–14.
Liu Jianjun, Chen Mingfeng, Ye Zipiao. The Estimation of the Non-Linear Model Parameter Based on Combination of Damped Least-Squares Method and Simulated Annealing Method[J]. Journal of Jinggangshan University(Natural Science),2010,31(6) : 10–14. |
| [8] |
金莉. 几种预测模型在高路堤沉降预测中的对比分析[J].
西部探矿工程,2006,(4) : 234–236.
Jin Li. Several Prediction Models in High Contrast to Analysis of Embankment Settlement Prediction[J]. West-China Exploration Engineering,2006,(4) : 234–236. |
 2016, Vol. 41
2016, Vol. 41

