| 一种双目混合追踪的视觉里程计算法 |
2. 地球空间信息协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
视觉里程计(visual odometry, VO)及视觉同步定位与建图(visual simultaneous location and mapping, V-SLAM)技术,弥补了GNSS系统在室内、遮挡等环境下精度较低的缺陷[1],是无先验、陌生环境下定位、定姿的一种有效技术手段, 在无人车、智能机器人、增强现实(augmented reality)等领域有着广泛的应用。
VO/V-SLAM算法大致可分为直接法和基于特征点的方法[2-3]。直接法假设同一路标点在不同帧的短时间观测内灰度保持不变,优化相机位姿以使影像光度差最小。文献[4]是直接法的代表性算法。基于特征点的方法通过匹配物方点、像方点,最小化重投影误差来确定位姿。特征点匹配有两种思路,一是计算描述子距离,距离最近的特征点一定程度上可认为是对同一地图点的观测;文献[5-7]算法提取影像的ORB(oriented brief)特征点进行配准,实现了多种影像传感器上完整的定位、建图、回环检测功能;另一种则是光流(optical flow)追踪算法,其假设同一像方点在相邻帧灰度不变且像素邻域有相同模式的微小运动,构建超定方程求解位移场进行追踪[8]。常用的光流有LK(Lucas-Kanade)及其变种Inverse Compositional光流[9-11]等, 后者在迭代时,方程左侧海森(Hessian)矩阵不变,提高了计算效率, 被广泛使用。文献[11]是使用光流追踪的典型算法。
特征点描述子的计算、匹配计算耗时长,描述子易受灰度、旋转、尺度等限制;光流追踪会累积误差,导致定位不准;而直接法跟踪丢失后重定位困难,地图无法有效复用。
针对以上问题,本文提出了一种使用光流和特征点混合追踪的算法。光流计算效率高,鲁棒性强;通过帧间极线约束,剔除定位粗差;关键帧提取特征点及描述子解决了跟踪丢失后重定位及地图复用的问题。
1 算法原理如图 1所示算法流程,初始化时,系统在初始化时提取双目ORB特征点,并在水平方向匹配描述子以获取同名点并计算路标点深度,直到某帧生成足够数量且深度适当的路标点。
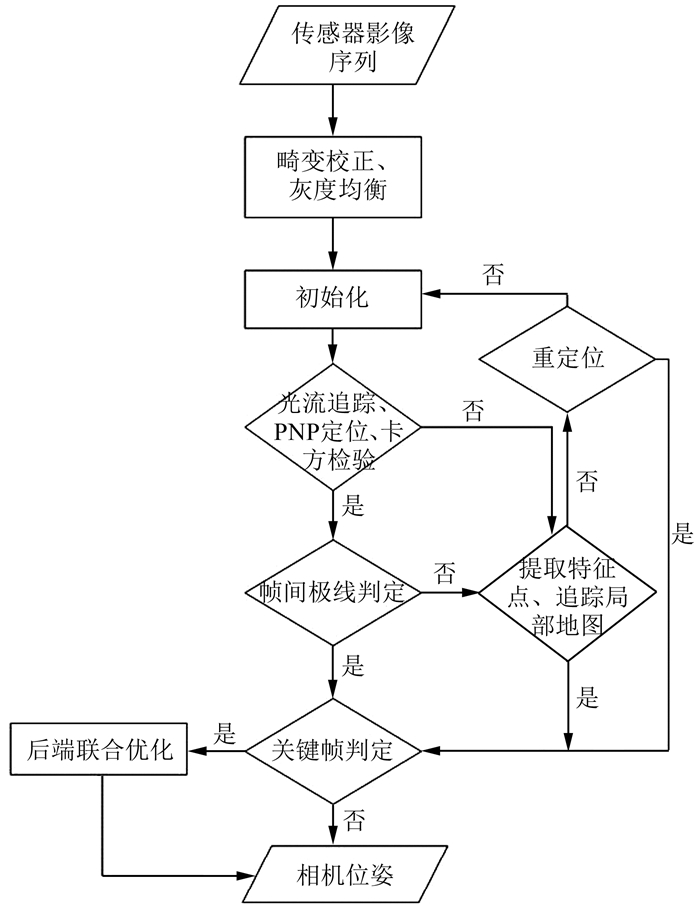 |
| 图 1 算法流程 Fig.1 Chart Flow of Algorithm |
1.1 追踪前端
在当前帧,优先采用Inverse Compositional光流追踪上一帧中追踪成功且通过检验的光流点。
设定相机成像时,在像平面每个方向(u, v)上存在标准差为一个像素的高斯噪声,可通过对每项重投影残差进行自由度为2的卡方检验来剔除光流追踪粗差[12],光流追踪会累积当前帧光流点相对于上一关键帧特征点的误差;此外,当前帧PNP(perspective n points)优化时初始位姿通过上一帧提供,在采样帧率低、相机高速运动(尤其是旋转)时,初始值欠佳,目标函数可能被错误优化,导致定位结果出现粗差;针对此问题,本文提出通过当前帧定姿后恢复的极线来探测定位粗差。
对于相邻两帧p和q,假设q成功追踪p并通过卡方检验的关键点有n个,PNP后优化得到的两帧在世界坐标系下旋转、平移为:Rp、Tp和Rq、Tq,则两帧相对位姿具有如下关系:
| $ \boldsymbol{R}_{p}^{q}=\boldsymbol{R}_{q} \boldsymbol{R}_{p}^{-1}, \boldsymbol{T}_{p}^{q}=\boldsymbol{R}_{q}^{-1}\left(\boldsymbol{T}_{p}-\boldsymbol{T}_{q}\right) $ | (1) |
结合相机内参矩阵K, 对每个在q帧追踪到的点,其对极几何应满足:
| $ \left.\boldsymbol{X}_{q}^{i \mathrm{~T}}\left(K^{-1}\right)^{\mathrm{T}}\left\lfloor\boldsymbol{T}_{p}^{q} \times\right\rfloor \boldsymbol{R}_{p}^{q} \boldsymbol{K}^{-1}\right) \boldsymbol{X}_{p}^{i}=0 $ | (2) |
式中,i表示第i个路标点;xqi、xpi为特征点的齐次坐标;
对每个xqi,计算它到对应极线的距离:
| $ t=\frac{\left|a_{i} x_{q}^{i}+b_{i} y_{q}^{i}+c_{i}\right|}{\sqrt{a_{i}^{2}+b_{i}^{2}}} $ | (3) |
式中,ai、bi、ci为(K-1)T
如图 2所示,车辆沿道路匀速行驶,算法输出的连续两帧相对位姿误差较小,追踪的光流点都在其帧间基础矩阵对应的极线上。
 |
| 图 2 满足极线约束的位姿 Fig.2 Pose Meets Epipolar Constraint |
在图 3中,光流追踪计算的位姿出现粗差,光流点同对应极线距离较远,此时需要对当前帧提取特征点,重新计算准确位姿。
 |
| 图 3 不满足极线约束的位姿 Fig.3 Pose doesn't meet epipolar constraint |
如果相邻帧极线判定失败,则提取ORB特征点及描述子进行追踪。本帧ORB特征点首先和上一关键帧特征点通过BOW(bag of word)加速关联[13];通过和上一关键帧和局部地图的匹配PNP计算精确位姿。特征点同路标点关联时,除了词袋、描述子的比较,还将要考虑视差距离、尺度及旋转一致性等,以减少误匹配。
1.2 后端优化为了维持追踪,算法将筛选关键帧(判据如当前光流跟踪点过少、相邻帧运动幅度大、长时间未插入关键帧等)并生成新的路标点。
每个路标点存储它被不同关键帧观测的信息(序列号、像素点坐标、当前帧描述子、可见金字塔层数阈值、平均观测角度等)。同时,每个关键帧维护它所观测到的路标点序列,以及同自身有共同观测点的帧的信息,维护共视帧(co-visible frame)集合。
关键帧插入后端联合优化时,其共视帧,帧所观察的路标点共同参与优化,构成优化问题:
| $ \left\{P_{j}, \xi_{k}\right\}=\arg \min\limits _{P_{j}, \xi_{k} }\sum\limits_{k \in K L \cup K F} \sum\limits_{j \in \lambda}\left\|Z_{k, j}-Z_{k, j}^{\mathrm{obs}}\right\|_{{\mathit{\Phi}}}^{2} $ | (4) |
式中,Pj、ξk为参与优化的路标点的位置和相机的位姿;KL、KF分别为当前帧邻接的共视帧和非邻接但包含共视点的关键帧[7],后者只参与计算,不进行优化;λ为关键帧同路标点的观测关系;Φ为重投影误差的权重。
联合优化后,对每项重投影残差进行卡方检验,剔除错误观测。
2 实验及分析本文使用了KITTI数据集[14, 15]对算法的定位精度和计算效率进行测试。处理所采用的计算机为Intel i7-7660U CPU,4G内存。
2.1 定位精度通过EVO工具评估算法定位精度。
测试KITTI-07序列,其水平轨迹、姿态(欧拉角表示)如图 4所示。图 4中,实线为本文算法计算值,虚线为真值。图 4(a)为车辆行驶水平轨迹,横、纵轴为距离,单位为m;图 4(b)为姿态(欧拉角表示),横轴为时间(帧数),纵轴分别为横滚角、俯仰角、偏航角,单位为(°)。
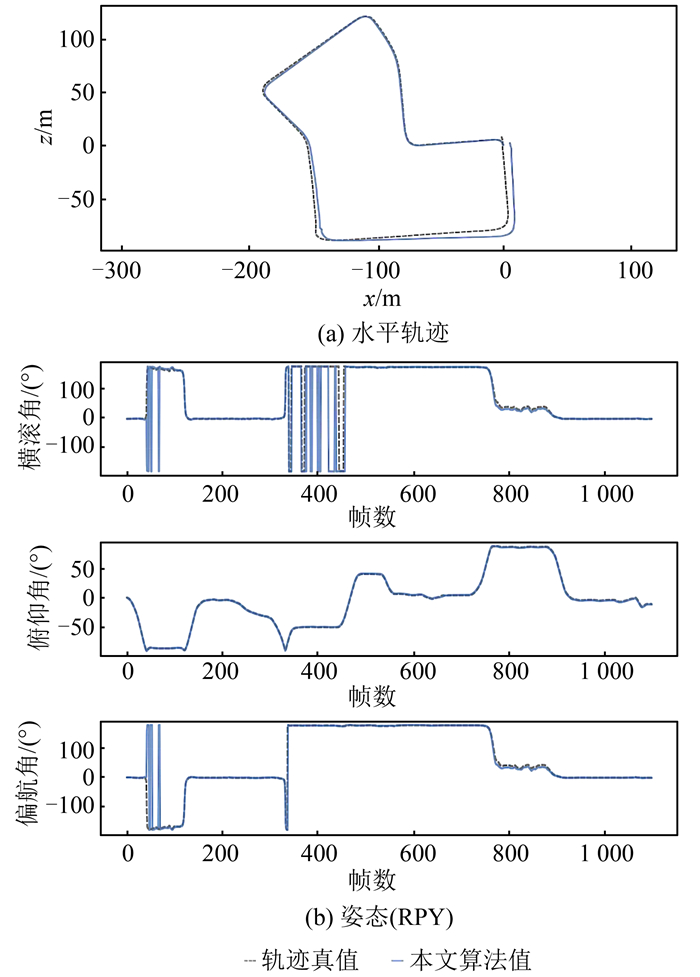 |
| 图 4 KITTI-07轨迹及姿态 Fig.4 Trajectory and Euler Angle of KITTI-07 |
本段轨迹长约695 m,终点处误差约为11.207 m,位置相对误差为1.61%;各方向定位精度约为6.80 m;定姿精度:欧拉角3个分量误差均约1°。
统计绝对误差,如图 5所示。
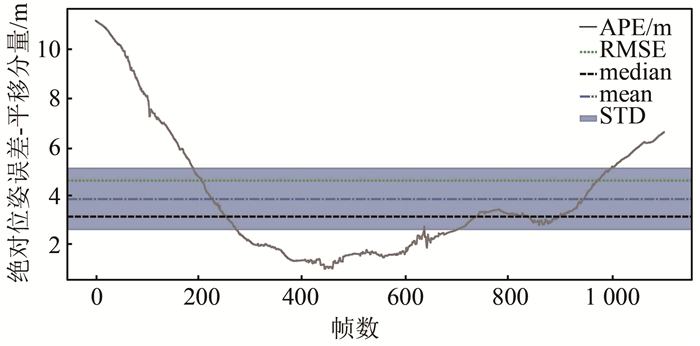 |
| 图 5 KITTI-07绝对误差 Fig.5 APE Error of KITTI-07 |
图 5为算法输出位姿同真值对齐(非首帧对齐)后的绝对位置误差的平移分量(absolute pose error,APE, )及其平均值(mean)、标准差(standard devitation, STD)等统计信息。在该序列下,算法最大误差为11.207 m,平均值为3.82 m,均方根误差(root mean square error, RMSE)为4.73 m。
测试KITTI-09序列,水平轨迹、姿态如图 6所示。
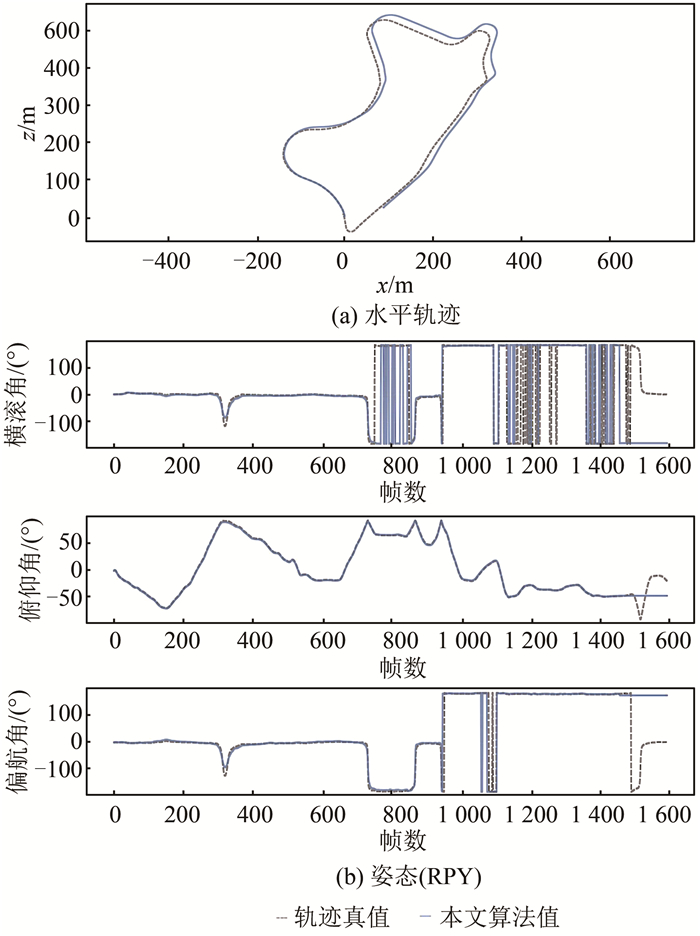 |
| 图 6 KITTI-09轨迹及姿态 Fig.6 Trajectory and Euler Angle of KITTI-09 |
此序列,车辆行驶转向多、光照多变,定位误差较大。在1 450帧左右由于车辆从亮处行驶至暗处,相机曝光变化大,导致算法跟踪丢失、定位失败。
本段轨迹丢失前误差约为41 m,位置相对误差为2.8%;各方向定位精度约为25 m;定姿精度约为3.9°。
统计算法处理KITTI数据集序列的定位精度,主要指标如表 1所示(剔除丢失位姿)。
| 表 1 KITTI数据集下算法平均定位精度 Tab.1 Algorithm's Localization Accuracy on KITTI |
 |
同ORB-SLAM2算法在无回环数据上表现相比,本文算法的定位、定姿指标:位置相对误差和角度相对误差均略低。
分析本文算法定位精度较ORB-SLAM2为代表的特征点算法之定位精度有所下降的原因:
1) 前端跟踪时,优先使用光流追踪,每一帧的光流均会累积小量误差,像方坐标随着系统运行而逐渐失准,导致位姿误差;而特征点法每帧全部重新提取特征点,避免了像方点误差累积;这是使用光流不可避免的;
2) 通过卡方检验进行光流追踪外点的剔除,约束较特征点法少;
3) 后端优化时,为了加速优化,未使用关联帧间全部观测约束,误差未有效分配。
通过以下方法可一定程度上提高定位精度:
1) 光流追踪后,首先使用两帧间光流点恢复的基础矩阵,Ransac剔除部分光流外点,再参与位姿BA解算;
2) 路标点深度使用逆深度的形式,其噪声更符合高斯分布的形式,更容易收敛;
3) 剔除外点时,除卡方检验外,设置更多其他约束条件。
2.2 计算效率关闭ORB-SLAM2回环检测线程,配置同样的ORB提取参数(每张影像提取2 000个特征点、8层金字塔、层间1.2倍降采样系数),和本文算法处理相同数据,处理KITTI-07像序列,统计每帧处理的耗时,结果如图 7所示。
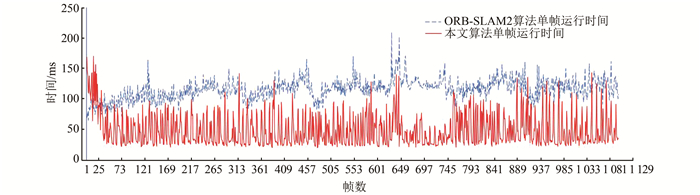 |
| 图 7 KITTI-07序列算法用时对比 Fig.7 Computation Time with KITTI-07 |
处理KITTI-09像序列,统计结果如图 8所示。
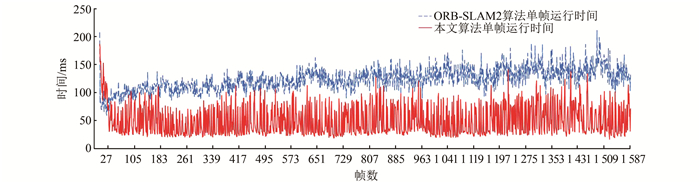 |
| 图 8 KITTI-09序列算法用时对比 Fig.8 Computation time with KITTI-09 |
统计算法处理KITTI数据集序列的耗时,本文算法单帧处理平均时间约55 ms;ORB-SLAM2(关闭闭环检测)单帧处理时间约120 ms。较ORB-SLAM2相比,处理效率有大约一倍的提升。使用光流追踪,避免了每帧固定的特征点提取、匹配操作,较大提高计算效率。
3 结束语本文提出的算法,使用Inverse Compositional光流加速跟踪过程,避免了特征点法的每帧的固定耗时操作,使用帧间位姿的对极几何约束剔除定位粗差,保证了计算效率和适当精度;另一方面,在光流追踪失败时,使用特征点追踪保证系统一定鲁棒性。建立的地图路标点具有描述子,可一定程度上实现重定位、地图复用。
目前,本文算法存在的问题,主要表现在后端优化时没有充分利用信息矩阵稀疏性加速优化;没能和惯性测量单元(inertial measurement unit, IMU)、GNSS等传感器进行融合处理,这将是下一步的研究目标。
| [1] |
卢维. 高精度实时视觉定位的关键技术研究[D]. 杭州: 浙江大学, 2015
|
| [2] |
Fraundorfer F, Scaramuzza D. Visual Odometry: Part Ⅰ: The First 30 Years and Fundamentals[J]. IEEE Robotics and Automation Magazine, 2011, 18(4): 80-92. DOI:10.1109/MRA.2011.943233 |
| [3] |
Engel J, Schöps T, Cremers D. LSD-SLAM: Large-scale Direct Monocular SLAM[C]. European Conference on Computer Vision, Switzerland, 2014
|
| [4] |
Engel J, Koltun V, Cremers D. Direct Sparse Odometry[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 611-625. DOI:10.1109/TPAMI.2017.2658577 |
| [5] |
Klein G, Murray D. Parallel Tracking and Mapping for small AR Workspaces[C]. Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, IEEE Computer Society, Washington, DC, USA, 2007
|
| [6] |
Mur-Artal R, Montiel J M M, Tardos J D. ORB-SLAM: Versatile and Accurate Monocular SLAM System[J]. IEEE Transactions on Robotics, 2015, 31(5): 1 147-1 163. DOI:10.1109/TRO.2015.2463671 |
| [7] |
Mur-Artal R, Tardós J D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras[J]. IEEE Transactions on Robotics, 2017, 33(5): 1 255-1 262. DOI:10.1109/TRO.2017.2705103 |
| [8] |
Forster C, Pizzoli M, Scaramuzza D. SVO: Fast Semi-direct Monocular Visual Odometry[C]. 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 2014
|
| [9] |
Strasdat H, Montiel J M M, Davison A J. Visual SLAM: Why Filter?[J]. Image and Vision Computing, 2012, 30(2): 65-77. DOI:10.1016/j.imavis.2012.02.009 |
| [10] |
Baker S, Matthews I. Lucas-Kanade 20 Years on: A Unifying Framework[J]. International Journal of Computer Vision, 2004, 56(3): 221-255. DOI:10.1023/B:VISI.0000011205.11775.fd |
| [11] |
Barfoot T D. State Estimation for Robotics[M]. UK: Cambridge University Press, 2017.
|
| [12] |
Gálvez-López D, Tardos J D. Bags of Binary Words for Fast Place Recognition in Image Sequences[J]. IEEE Transactions on Robotics, 2012, 28(5): 1 188-1 197. DOI:10.1109/TRO.2012.2197158 |
| [13] |
Qin T, Li P, Shen S. Vins-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator[J]. IEEE Transactions on Robotics, 2018, 34(4): 1 004-1 020. DOI:10.1109/TRO.2018.2853729 |
| [14] |
Geiger A, Lenz P, Urtasun R. Are We Ready for Autonomous Driving? The Kitti Vision Benchmark Suite[C]. 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 2012
|
| [15] |
Lenz P, Ziegler J, Geiger A, et al. Sparse Scene Flow Segmentation for Moving Object Detection in Urban Environments[C]. Intelligent Vehicles Symposium, IEEE, Baden, Germany, 2011
|
 2021, Vol. 46
2021, Vol. 46

