| WiFi辅助下附有高程先验信息的GNSS定位 |
2. 武汉大学卫星导航定位技术研究中心,湖北 武汉,430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
全球导航卫星系统(global navigation satellite system, GNSS)已经成为时空信息获取的主要技术手段之一,其在测绘、交通运输、精细农业、授时与时间同步等领域都有着广泛的应用。然而,在城市峡谷等典型复杂环境下,卫星信号容易被遮挡,由于观测卫星数量不足而导致无法正常定位的情况时有发生,目前已有的解决方案包括以下两个方面:①减少求解未知参数的个数,如通过外加高精度时钟[1]或者钟差预报[2]的方法来避免求解接收机钟差参数;通过附加高程信息[3]将三维定位问题简化为二维定位。②多种定位技术融合,常见的有GNSS与惯性导航系统(inertial navigation system, INS)[4],GNSS与基于多传感器的航迹推算(dead reckoning, DR)[5],GNSS与伪卫星[6],GNSS与手机基站信号[7],GNSS与泛在无线信号[8, 9]等。本文在文献[10]的基础上,进一步讨论了城市典型泛在无线信号WiFi(wireless fidelity)辅助下附有高程信息的GNSS定位,利用WiFi定位获取概略平面位置信息,在此基础上,通过先验高程信息来进行卫星数量不足情况下的GNSS定位,并研究了先验高程精度对定位结果的影响。
1 附有高程先验信息的GNSS定位附有高程先验信息的单系统GPS定位的基本原理可以参看文献[10],GNSS多系统定位原理和单系统基本相同,由于不同卫星定位系统所采用的时间基准不尽相同,因此,需要考虑彼此时间系统之间的偏差问题,以BDS(BeiDou navigation satellite system)和GPS为例,基于测码伪距观测值的标准单点定位观测方程为:
| $ \left\{ \begin{array}{l} \tilde \rho = \rho + c({\rm{d}}{t_i}{\rm{d}}{t^j}) + {d_{{\rm{iono}}}} + {d_{{\rm{trop}}}} + \varepsilon \\ \rho = {\rm{ }}\sqrt {{\rm{(}}{X_i}{X^j}){^2} + {\rm{ (}}{Y_i}{Y^j}{)^2} + {\rm{ (}}{Z_i}{Z^j}){^2}} \\ \tilde \rho \prime = \rho \prime + c({\rm{d}}{t_i}{\rm{d}}t{\prime ^j}) + \mathit{c}{\mathit{t}_{{\rm{bias}}}} + d{\prime _{{\rm{iono}}}} + d{\prime _{{\rm{trop}}}} + \varepsilon \prime \\ \rho \prime = {\rm{ }}\sqrt {{\rm{(}}{X_i}X{\prime ^j}){^2} + {\rm{ (}}{Y_i}Y{\prime ^j}){^2} + {\rm{ (}}{Z_i}Z{\prime ^j}){^2}} \end{array} \right. $ | (1) |
式中,
与单系统单点定位相比,多系统观测方程增加了时间系统偏差tbias,和接收机钟差类似,它通常与接收机位置一起被当作未知参数来求解。因此,利用双系统定位至少需要观测到5颗及以上的导航卫星,双系统以上的卫星定位可以依此类推。附有高程信息的双模卫星观测方程为:
| $ \begin{array}{l} \;\;\;\;\left[ \begin{array}{l} {\varepsilon _1}{\rm{ }}\\ \vdots \\ {\varepsilon _m}\\ \varepsilon \prime {_1}\\ \vdots \\ \varepsilon \prime {_n} \end{array} \right] = \left[ \begin{array}{l} {a_1}\;\;{b_1}\;\;\;{c_1}\;\;1\;\;0\\ \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {a_m}\;\;{b_m}\;\;{c_m}\;\;1\;\;0\\ a\prime {_1}b\prime {_1}\;c\prime {_1}\;1{\rm{ }}\;1\\ a\prime {_n}\;b\prime {_n}\;c\prime {_n}\;1{\rm{ }}\;1 \end{array} \right] \times \\ \left[ \begin{array}{l} {j_{11}}\;\;{j_{12}}\;\;0\;\;0\\ {\rm{ }}{j_{21}}\;\;{j_{22}}\;\;0\;\;0\\ {j_{31}}\;\;{j_{32}}\;\;0\;\;0\\ \;0\;\;\;\;0\;\;\;\;1\;\;0\\ \;0\;\;\;\;0\;\;\;\;0\;\;1 \end{array} \right] \times \left[ \begin{array}{l} {\rm{d}}L\\ {\rm{d}}B\\ c{\rm{d}}{t_i}\\ c{\rm{d}}{t_{{\rm{bias}}}} \end{array} \right] - \left[ \begin{array}{l} {l_1}\\ \vdots {\rm{ }}\\ {l_m}\\ l\prime {_1}\\ \vdots \\ {\rm{ }}l\prime {_n} \end{array} \right] \end{array} $ | (2) |
式中,ai(a′i)、bi(b′i)和ci(c′i)为观测方程线性化系数;jij为空间直角坐标和大地坐标微分关系式中雅可比矩阵对应的元素,详细表达式可参看文献[10];dL和dB分别为大地经纬度改正数;li(l′i)为观测方程线性化后的观测值与计算值之差OMC(observed minus computed);m和n分别表示GPS卫星和BDS卫星的个数。
令
| $ \begin{array}{l} \;\;\;\;\;\mathit{\pmb{V}} = {\left[ {{\varepsilon _1} \ldots {\rm{ }}{\varepsilon _m}\varepsilon \prime {_1} \ldots {\rm{ }}\varepsilon \prime {_n}} \right]^{\rm{T}}}{\rm{ }},\\ \;\;\;\;\;\;\;\mathit{\pmb{L}} = {[{l_1} \ldots {\rm{ }}{l_m}l\prime {_1} \ldots {\rm{ }}l\prime {_n}]^{\rm{T}}}{\rm{ }},\\ \;\;\;\;\;\;\;\;\mathit{\pmb{X}} = {[dLdB{\rm{ }}cd{t_i}d{t_{}}bias]^{\rm{T}}},\\ \mathit{\pmb{A}} = \left[ \begin{array}{l} {a_1}\;\;{b_1}\;\;{c_1}\;\;1\;\;0\\ \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {a_m}\;{b_m}\;\;{c_m}\;1\;\;0\\ a\prime {_1}\;b\prime {_1}\;c\prime {_1}\;\;1\;1{\rm{ }}\\ a\prime {_n}\;b\prime {_n}\;c\prime {_n}\;1\;\;1 \end{array} \right]{\rm{ }} \times {\rm{ }}\left[ \begin{array}{l} {j_{11}}\;\;{j_{12}}\;\;0\;\;0\\ {\rm{ }}{j_{21}}\;\;{j_{22}}\;\;0\;\;0{\rm{ }}\\ {j_{31}}\;\;{j_{32}}\;\;0\;\;0\\ \;0\;\;\;\;\;0\;\;\;1\;\;0\\ \;0\;\;\;\;\;0\;\;\;0\;\;1 \end{array} \right] \end{array} $ |
则式(2)可以写成式矩阵的形式为:
| $ \mathit{\pmb{V}}{\rm{ = }}\mathit{\pmb{AX}}- \mathit{\pmb{L}} $ | (3) |
当只有4颗观测卫星时,则令V=0,通过直接解线性方程组(3)来求出最后的结果为:
| $ \mathit{\pmb{X}}{\rm{ = }}{\mathit{\pmb{A}}^{{\rm{ - 1}}}}\mathit{\pmb{L}} $ | (4) |
在进行附有高程先验信息的卫星定位时,除了要知道定位用户的大地高之外,还需要知道其概略的经纬度或经过地图投影后的平面坐标。随着无线通讯技术的发展和移动互联网时代的到来,城市中无线局域网络(wireless local area networks, WLAN)/WIFI技术的普及率愈来愈高,因此, 本文通过WiFi定位的方法来获取定位用户的概略经纬度。目前广泛使用的基于WiFi信号的定位方法有加权质心法、几何交会法[11]和基于指纹库的模式匹配法[12] 3种,笔者采用算法较为简单的加权质心法来得到初始位置为:
| $ L = \frac{{\sum\limits_{i = 1}^n {\frac{{{L_i}}}{{{{\left| {{\rm{RSS}}} \right|}_i}}}} }}{{\sum\limits_{i = 1}^n {\frac{1}{{\left| {{\rm{RS}}{{\rm{S}}_i}} \right|}}} }},B = \frac{{\sum\limits_{i = 1}^n {\frac{{{B_i}}}{{{{\left| {{\rm{RSS}}} \right|}_i}}}} }}{{\sum\limits_{i = 1}^n {\frac{1}{{\left| {{\rm{RS}}{{\rm{S}}_i}} \right|}}} }} $ | (5) |
式中,n表示用户端无线网卡所探测到的WiFi热点的个数;Li与Bi分别表示第i个WiFi热点的大地经度和大地纬度,单位为弧度;RSSi表示无线网卡所观测到的第i个WiFi热点的信号强度值,单位为dBm;L与B为用户最后的定位结果。在利用WiFi定位获取初始经纬度后,结合附加的高程信息,在双系统定位模式下,当只观测到4颗导航卫星时,利用相应的伪距观测值可以列出观测方程式(2)和式(3),通过式(4)就可以得到定位结果,由于初始位置精度有限,因此, 在计算过程中往往需要迭代运算,直至定位结果收敛为止。
3 实验与结果分析 3.1 实验方案设计为了验证WiFi辅助下附有高程信息的卫星定位的可行性,本文设计了一组仿真实验,实验场地为学校广场,定位实验分为静态定位和动态定位两个部分。
整个实验过程分两步进行:首先,在静态定位观测点静态观测1 h;然后,推着实验小车从该点出发,移动到动态定位的终点后停止观测。整个过程中,GNSS观测值和WiFi热点的信号强度值的采样率均为1 s。
在利用WiFi信号进行定位时,需要知道WiFi热点的坐标值,由于本实验采用周围环境中已经布设的无线局域网信号,其热点位置是未知的,所以还需要进行WiFi热点坐标的反算。War-Driving是反推WiFi热点坐标较常用的方法,该方法通过驾驶配备有GPS和WiFi信号采集模块的汽车沿着街道扫描周围的WiFi热点,同时记录下各WiFi信号强度值和相应的GPS定位结果,经过数据处理后,可以得到WiFi热点的概略坐标值。本实验的做法和War-Driving类似,通过步行的方法沿路扫描周围环境中的WiFi热点,该方法通常被称为Walk-Driving。
定位解算分单系统GPS三星定位、单系统BDS三星定位、双系统GPS加BDS四星定位3种模式,其中,GPS卫星和BDS卫星的数量相等,均为两颗。GPS采用的是WGS(world geodetic system)84坐标系,而BDS采用的是2000国家大地坐标系,两者是相容的,在cm级定位时,可以忽略两者之间的差异[13]。定位坐标参考值通过与附近GNSS连续跟踪站的观测数据进行差分处理获得;定位点的初始平面坐标通过WiFi定位得到;附加高程信息从定位坐标参考值中提取,为了便于分析,将坐标参考值和最后定位结果通过高斯投影扩展到平面上,投影带为3°带。
3.2 静态定位WiFi辅助下附有高程信息的GPS和BDS单系统三星静态定位偏差及GPS与BDS混合四星静态定位偏差如图 1所示。
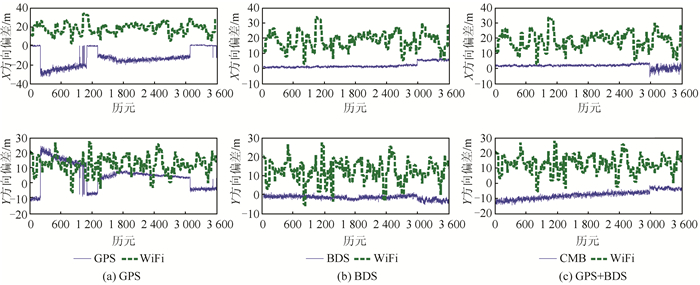 |
| 图 1 WiFi辅助下GPS、BDS、GPS+BDS静态定位偏差 Fig.1 WiFi Assisted GPS, BDS and GPS+BDS Static Positioning |
图 1(a)中,曲线表示GPS定位结果在水平方向上的偏差,点状线表示WiFi定位结果在水平方向上的偏差。WiFi与GPS定位偏差都出现了跳变现象,如在WiFi定位中,从第59个历元到第60个历元,Y方向的定位偏差从19.276 m变为7.901 m;在GPS定位中,从第199个历元到第200个历元,X方向的定位偏差从-0.069变为-25.219 m。对于WiFi定位而言,产生跳变的原因主要是由于其所观测到的WiFi热点的个数发生变化而引起的,其第59个历元观测到了13个WiFi热点,而到了第60个历元,WiFi热点数则上升到了18个。对于GPS定位而言,偏差跳变主要是由定位过程中所使用GPS卫星的PRN(pseudo random noise)号发生变化而引起的,其第199个历元定位所用的卫星的PRN号为26、16和27,到了第200个历元,卫星号的PRN号为26、16和31。
图 1(b)中, 曲线表示BDS定位结果的偏差,与GPS结果相比,BDS定位结果跳变次数明显减少,跳变的程度也有所降低。发生跳变的历元为2 973,其X方向的偏差从上个历元的1.736 m变为5.993 m;定位所使用的卫星的PRN号也从7、3和2变为7、10和8,其中2、3号卫星为地球同步轨道(geostationary earth orbit,GEO)卫星,与地球相对静止,而其他卫星则为倾斜地球同步轨道(inclined geosynchronous satellite orbit,IGSO)卫星。
图 1(c)中, 曲线CMB(combined)表示GPS与BDS双模混合定位结果,整个定位过程中只发生了一次定位结果的跳变,发生在第2 973历元,X方向的定位偏差由上个历元的2.894 m变为-3.933 m,原因也是由于定位所使用的卫星发生变化而引起的。整个定位过程中,GPS卫星没有发生变化,一直是PRN号为16和26的两颗卫星;而BDS卫星则从PRN号为7和3的两颗卫星变为了7和10。3种模式下定位偏差相关的统计结果如表 1所示。
| 表 1 静态定位偏差统计/m Tab.1 Statistics of Static Positioning Bias/m |
 |
从表 1中可以看出,附有高程信息的卫星定位与WiFi定位相比,其统计定位精度RMS(root mean square)均有不同程度地提高:GPS定位的X方向和Y方向分别提高了约19.98%和29.15%;BDS定位的X方向和Y方向分别提高了约87.03%和83.74%;双模混合定位的X方向和Y方向分别提高了约89.27%和34.85%。除了GPS定位外,BDS和双模定位偏差的波动均小于WiFi定位,定位的波动主要和卫星几何分布变化大小相关,由于GPS卫星是中轨卫星,而BDS卫星为GEO和IGSO,其空间几何变化较GPS卫星而言要缓和些。
静态定位偏差累积分布图如图 2所示。
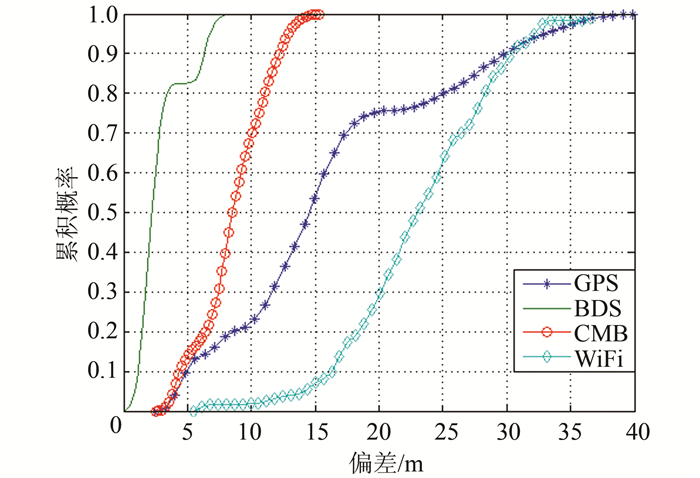 |
| 图 2 静态定位偏差累积分布 Fig.2 Cumulative Distribution of Static Positioning Bias |
图 2中可以看出,在WiFi定位给出水平方向定位初值后,附有高程信息的BDS三星定位效果最好,其水平方向定位偏差都在10 m以内;其次是GPS与BDS双模混合定位,水平方向偏差小于15 m;GPS定位效果最差,有些历元的定位精度甚至低于WiFi定位,主要是由于其卫星几何分布不均匀所造成的,如果所观测的卫星分布过于集中,会导致观测方程系数矩阵接近奇异阵,定位精度会显著下降。
3.3 动态定位GPS和BDS三星动态定位偏差及GPS与BDS双模四星动态定位偏差如图 3所示。
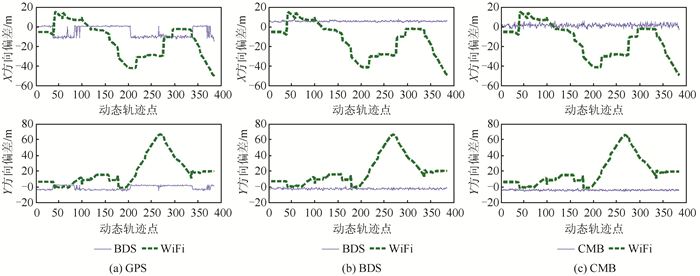 |
| 图 3 GPS、BDS、GPS+BDS动态定位偏差 Fig.3 GPS, BDS and GPS+BDS Kinematic Positioning |
从图 3(a)中可以看出,动态定位中,WiFi定位和GPS定位偏差仍然存在跳变现象。对于GPS定位而言,其定位精度的变化和卫星的几何分布的变化息息相关。定位偏差在第36个轨迹点发生了较大变化,当前定位使用的卫星的PRN号从上个轨迹点的16、26、27变为16、26、31,和静态定位类似,虽然发生定位偏差跳变点的卫星高度较高,但是几何分布没有之前的均匀,导致定位精度发生变化,X方向的定位偏差从上个点的1.197 m变为-10.175 m。
从图 3(b)中可以看出,BDS定位结果总体较稳定,没有发生跳变现象,主要原因是其定位使用的卫星的几何分布基本上没有发生太大的变化,而且分布也较为均匀。
从图 3(c)中可知,在整个定位过程中,所使用卫星的几何分布没有发生较大变化,定位精度也较稳定。与单系统定位不同,从卫星天空视图上看,虽然GPS卫星和BDS卫星分布比较集中,但是由于GPS是中轨卫星,轨道高度约为2万多公里,BDS则为GEO或者MEO,轨道高度约为3万多公里,这种高低轨道结合的模式在某种程度上避免了单系统定位中方程系数矩阵的奇异问题。因此,对于卫星数量不足且对其几何分布有较高要求的定位问题,基于多系统且具有不同类型轨道的卫星定位较单系统而言更具优势。动态定位偏差相关统计结果如表 2所示。
| 表 2 动态定位偏差统计/m Tab.2 Statistics of Kinematic Positioning Bias/m |
 |
从表 2可以看出,动态定位与静态定位类似,与WiFi定位相比,卫星定位统计精度RMS均有不同程度的提高。GPS三星动态定位X方向和Y方向分别提高了约65.92%和88.76%;BDS三星动态定位X方向和Y方向分别提高了约73.98%和86.45%;双系统四星动态定位X方向和Y方向分别提高了约89.55%和83.90%。WiFi定位偏差波动最大,BDS三星定位波动最小,这可以从标准差中体现出来。定位偏差的累积分布如图 4所示。
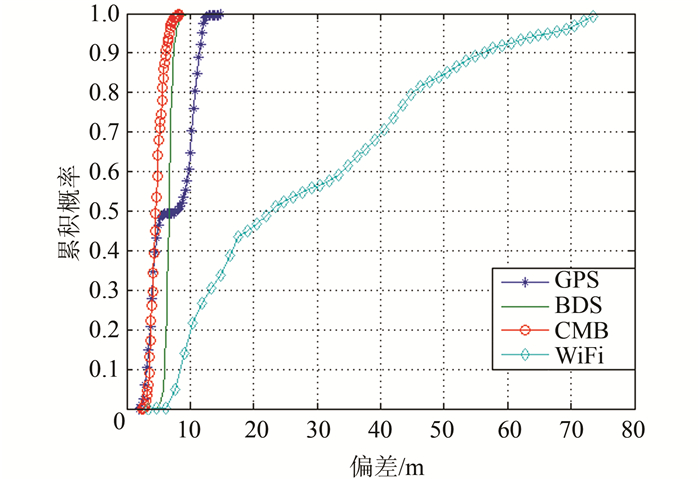 |
| 图 4 动态定位偏差累积分布示意图 Fig.4 Cumulative Distribution of Kinematic Positioning Bias |
从图 4可以看出,动态定位情况下,双系统四星定位效果最好,其次是BDS三星定位,其定位偏差都小于10 m;GPS三星定位偏差则在15 m以内。与静态定位相比,不同模式下卫星定位精度更为接近,一方面是由于GPS卫星的几何分布得到改善;另一方面可能是由于定位用户在运动过程中,BDS定位精度有所下降(可能是由于卫星几何分布变化引起),使得GPS与BDS定位偏差变得较为接近。
3.4 高程精度对定位结果的影响附有高程信息的卫星定位,前提条件之一就是要得到高程信息,因此,有必要讨论下高程精度对定位结果的影响。由前面的数据处理可知,BDS三星静态定位时,卫星几何分布较均匀,定位精度最高且较为稳定,为了减少其他因素对定位结果的影响,采用该数据作为示例数据。卫星单点定位高程的精度一般在30 m以内[14],普通城市范围内的平均高差也不会超过50 m。因此本文计算了±50 m之内的高程精度对定位结果的影响,并求出了定位偏差的RMS值,相关结果如图 5所示。
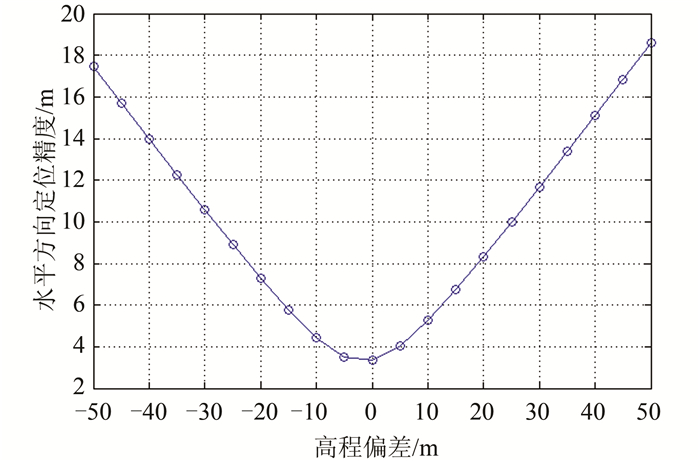 |
| 图 5 高程偏差对定位的影响 Fig.5 Influence of Geodetic Height Bias on Positioning Accuracy |
从图 5中,可以看出,水平方向定位精度随着高程偏差的增加而不断降低,且偏差的符号与定位精度关系不大,如高程方向10 m的偏差与-10 m的偏差对定位的影响基本相等,其差异不会超过2 m。
4 结束语WLAN/WiFi辅助下附有高程信息的卫星定位是利用大地坐标与空间直角坐标之间的微分关系,将卫星定位中基于伪距观测值的单点定位方程写成以大地坐标作为未知参数的形式,当大地高已知时,可以减少必要的卫星观测数,从而可以解决卫星观测数不足的定位问题。在定位解算的过程中,还需要知道概略的二维位置信息,考虑到“无线城市”建设的大背景,利用城市已有的建设成果,可以通过WiFi定位的方法来获取所需的二维坐标。仿真实验的结果表明,在WiFi定位给出初始概略二维坐标后,再进行附有高程信息的卫星定位,与单独的WiFi定位相比,其定位精度有所提高。与常规的单点定位类似,卫星的几何分布对定位结果有较大影响。当卫星分布均匀时,所获得的定位偏差也较小。当导航卫星分布过于集中时,观测方程系数矩阵条件数增大,矩阵接近病态,所得到的解也会产生较大误差,这一点可以从实验中BDS与GPS定位结果看出,由于BDS卫星分布较均匀分散,其定位偏差的RMS明显小于GPS。另外,在多系统定位模式下,当导航卫星的轨道分布差异较大时,如在GPS和BDS的双系统四星定位过程中,由于GPS使用的是MEO卫星,而BDS使用的是GEO或者IGSO卫星,即使卫星分布较集中,也可以获得不错的定位结果。高程的精度也会对定位结果产生影响,当高程偏差增大时,其相应的定位精度也会随之降低,在无法获得精确的高程信息的情况下,可以用概略高程(如偏差小于10 m)来进行单系统三星定位或者双模四星定位,仍然可以满足普通导航定位的需求。
致谢
感谢武汉大学卫星导航定位技术研究中心的牛小骥教授带领的GNSS/INS研究小组在数据采集阶段所提供的帮助。
| [1] |
Sturza M. GPS Navigation Using Three Satellites and a Precise Clock[J]. Journal of the Institute of Navigation, 1983, 30(2): 122-132. |
| [2] |
滕云龙, 师奕兵, 郑植. GPS不完整星座定位方法研究[J]. 宇航学报, 2011, 32(1): 93-97. DOI:10.3873/j.issn.1000-1328.2011.01.014 |
| [3] |
Phatak M, Chansarkar M, Kohli S. Position Fix from Three GPS Satellites and Altitude:A Direct Method[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 350-354. DOI:10.1109/7.745705 |
| [4] |
Gao Zhouzheng, Zhang Hongping, Ge Maorong, et al. Tightly Coupled Integration of Multi-GNSS PPP and MEMS Inertial Measurement Unit Data[J]. GPS Solutions, 2017, 21(2): 377-391. DOI:10.1007/s10291-016-0527-z |
| [5] |
Tsakiri M, Kealy A, Stewart M. Urban Canyon Vehicle Navigation with Integrated GPS/GLONASS/DR Systems[J]. Navigation-Journal of the Institute of Navigation, 1999, 46(3): 161-174. |
| [6] |
Li Y, Rizos C.Triple Integration of GPS, Locata and INS for Seamless Integrated Navigation in Urban Environments[C]. China International Conference on Inertial Technology and Navigation, Nanjing, China, 2010
|
| [7] |
Son H C, Lee J G, Jee G I.Mobile Station Location Using Hybrid GPS and a Wireless Network[C].The 57th IEEE Semiannual Vehicular Technology Conference, Jeju, South Korea, 2003
|
| [8] |
Mok E, Retscher G, Xia Linyuan.Investigation of Seamless Indoor and Outdoor Positioning Integrating WiFi and GNSS[C].XXⅢ International FIG Congress, Munich, Germany, 2006
|
| [9] |
马燕, 袁蔚林, 陈秀万, 等. 基于WiFi与GPS组合定位算法的无缝定位方法研究[J]. 地理与地理信息科学, 2013, 29(3): 6-9. |
| [10] |
夏敬潮, 叶世榕, 刘炎炎, 等. WiFi辅助下附有高程信息的GPS定位[J]. 武汉大学学报·信息科学版, 2014, 39(1): 52-55. |
| [11] |
朱律, 沈云中. WiFi室内距离交会定位位置的迭代解法[J]. 测绘地理信息, 2017, 42(4): 58-60. |
| [12] |
薛卫星, 邱卫宁, 花向红, 等. RSSI信号特征值对WiFi室内定位精度的影响分析[J]. 测绘地理信息, 2016, 41(4): 23-26. |
| [13] |
魏子卿. 2000中国大地坐标系及其与WGS84的比较[J]. 大地测量与地球动力学, 2008, 28(5): 1-5. |
| [14] |
唐卫明, 徐坤, 金蕾, 等. 北斗/GPS组合伪距单点定位性能测试和分析[J]. 武汉大学学报·信息科学版, 2015, 40(4): 529-533. |
 2019, Vol. 44
2019, Vol. 44

