| 静态室内路径规划的改进A-Star算法 |
静态环境的显著特点是预先知晓环境中的障碍物信息[1]。室内地图即属典型的静态环境,其特点是各类特征点种类多,信息量大,拓扑关系复杂。目前较为成熟的静态环境的路径规划与导航算法主要有以下3类: ① Dijkstra最短路径算法类,由于Dijkstra算法是基于遍历完的所有节点才得到最短路径,因此通过这种方法得到最短路径的成功率很高,但是遍历节点越多时,其效率就会相应越低[2]。对于拥有大量的拓扑关系的室内地图而言,这种方法耗时较多。② 图形学建模类,借助了图形学中建模的思想,并且将存储量较大、结构复杂的图形信息转化为存储量小、结构较简单的数学表达形式,具有直观、高效的优点,但是由于图形建模的思想在搜索能力方面有着先天性的不足[3],因此,面对室内地图中复杂的路径、障碍物信息,这种算法难以胜任。③ 迭代随机式搜索类,其特点是对目的地进行多线并行搜索, 并同时对多个可行解进行检查,一般不会陷入局部的极小点,其结果的可信度较高[4]。但是针对随机式的搜索方案,影响其搜索效率的最主要因素是编码长度和搜索空间[5]。由于针对不同静态环境的室内地图需要设置不同的编码,增大了路径规划大范围应用时的成本。此外,该类算法的随机性使得对于同一组起终点,规划的路径可能不同,这也不利于用户体验。
针对上述问题,本文选用基于启发式搜索的A-Star算法,通过对室内地图进行预处理,对可行域进行优化,对A-Star算法遍历模式进行改进,并利用启发式搜索的方式设置合适的估价函数,对搜索的位置进行评估,大大减少了不必要的搜索,降低成本的同时能够保证耗时较少。
1 A-Star算法原理与实现流程A-Star算法是一种静态路网中求解最短路径最有效的方法[6]。其基本思想是:采用启发式搜索的方式选择合适的启发函数, 对于各个扩展节点的代价值进行计算和评估, 从而选择代价值最优的结点加以扩展, 直到找到目标节点为止[7]。
A-Star算法评价周围各节点的估值时需要用到估价函数,其一般形式为:
| $f\left( n \right)=g\left( n \right)+h\left( n \right)$ | (1) |
式中,f (n)为估价函数,是起点经过节点n到达终点的最优估计值;g (n)是从初始节点到节点n的实际消耗;h (n)是从节点n到目标点的估计消耗,体现了搜索的启发式信息,因此,h (n)被称为启发性函数[8]。本文以曼哈顿距离作为室内地图规划的启发函数,其表达式为:
| $h\left( n \right)=\left| {{X}_{i}}-{{X}_{j}} \right|+\left| {{Y}_{i}}-{{Y}_{j}} \right|$ | (2) |
为了保证A-Star算法总能找到最小代价路径, 进行搜索的图必须满足如下条件:① 搜索图中的每个节点的后继节点的数目是有限的;② 搜索图中所有弧的代价都大于某个正数ε;③ 对于搜索图中的所有节点n, h (n)不会超出实际值h (n)的估计[9]。
A-Star算法的工作原理中需要用到两个列表:openlist列表和closelist列表。openlist列表用来记录所有被计算过但未扩展过的节点,closelist列表中用来记录已经被扩展过的节点[10]。每次搜索中,根据openlist列表里各节点估价函数f (n)值大小进行排序,删除f (n)值最小的节点,并添加到closelist列表中,然后对其进行扩展,依次循环,直到搜索到目标节点。A-Star算法的流程图如图 1所示。
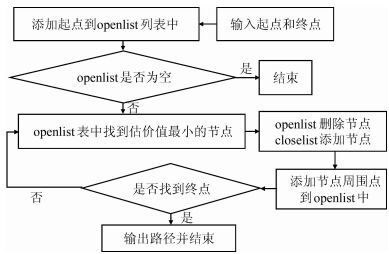 |
| 图 1 A-Star算法流程图 Figure 1 Flow Chart of A-Star Algorithm |
A-Star算法在搜寻过程当中,需要将周围8个方向的待选点用预先设定的估价函数进行估价并排序。在此过程中,其运算速率和存储效率主要取决于循环遍历的运算速率和存储效率。通过将list表的循环遍历方式设置为倒序遍历, 使得算法能快速地找到新添加的节点,在运算效率和存储效率上更为高效,从而加快目标点搜索的效率。
2 静态室内路径规划关键问题处理方法 2.1 运用Grid法进行室内地图预处理由于A-Star算法的路径规划需使用数字化后机器识别的地图(一般使用数组或堆表示)进行搜索。借鉴图形学中Grid法建模的方式,将室内地图用0、1分别标记室内地图中的可通行域和不可通行域。采用0、1的数字存储模式后的数字化地图,室内地图按照矩形格网划分,其路径点在矩形格网中呈均匀分布。因此,使用曼哈顿距离作为A-Star算法的估价函数,其搜寻效率会明显优于欧氏距离估值函数。在空间占用和算法效率上的优化幅度非常明显,图 2为原始室内地图,图 3给出了建模后图像。未采用Grid法建模前的室内地图文件体积为56.4 kB,采用Grid法建模后的数据文件体积为1.46 kB (室内地图文件格式:png,画幅:2 400像素×1 600像素,颜色模式:RGB)。
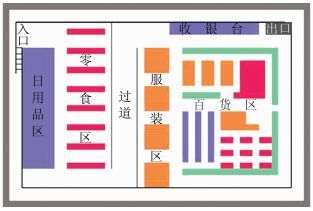 |
| 图 2 原始室内地图 Figure 2 Original Indoor Map |
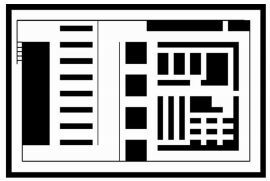 |
| 图 3 Grid法预处理后的室内地图 Figure 3 Indoor Map Preprocessed with Grid Method |
2.2 可行域线性化处理方法
由于A-Star算法采用启发式搜索,因此其一个显著的特点是:在障碍物附近,其搜索速度会显著加快,而在宽阔的可行域附近,其搜索速度会明显变慢[11]。利用A-Star算法的这一特点,将可行域进行线性化处理,从而加速路径搜索效率。
将室内地图(图 2)的可行域部分的色彩进行颜色识别(室内地图中的可行域部分对应颜色为白色,RBG代码为#FFFFFF),并从可行域两端开始向中间收拢,直至形成线性连通可行区域(需要用阈值进行判定,如示例图中判定方式为当路径宽度小于等于2像素时停止收缩)。图 4为可行域线性化处理后的可行域(图 4的实际路径宽度为2像素,为了显示效果,对路径做了加粗处理)。
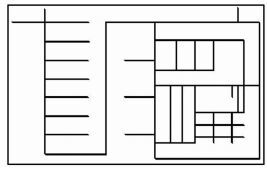 |
| 图 4 可行域线性化后的室内地图 Figure 4 Indoor Map After Linearization of Feasible Region |
为了直观评估可行域线性化处理的效果,采用小米手机(小米Mi5,内存:3 GB,CPU单核最大主频1.8 GHz (4核))和监测软件Android emulator monitor 2.1.2进行测试。图 5给出了测试结果截图。从图 5可以看出,采用可行域线性化后,CPU占用峰值出现了显著的下降,CPU载荷运算时间明显缩短,内存占用也大为降低,优化效果非常明显。
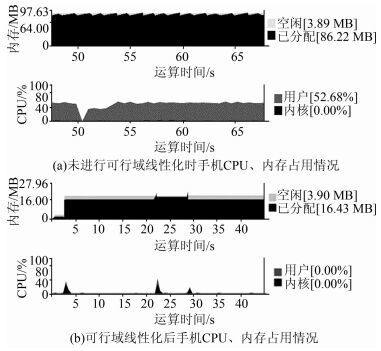 |
| 图 5 可行域线性化前后手机CPU、内存占用情况 Figure 5 CPU, Memory Usage Before and After Linearization of Feasible Region |
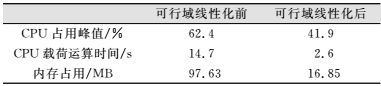
表 1为通过监测软件获得的具体提升数据,通过此方法进行优化处理,CPU占用峰值下降32.85%,CPU载荷运算时间下降82.31%,内存占用下降82.74%,优化效果显著(数据仅供参考,实际优化率与手机性能有关,下同)。
| 表 1 可行域线性化前后数据对比 Table 1 Data Comparison Before and After Linearization of Feasible Region |
 |
2.3 A-Star算法运算速率和存储效率的优化方法
经过测试,将循环遍历方式设置为倒序遍历,即对list表中由最后一位开始遍历到第一位[12]。将添加到openlist列表中的新节点存放在列表的最后几位,搜索效率有了明显的提升。图 6给出了处理前后监测软件数据截图。从图 6可知,采用倒序遍历后,CPU占用峰值有所下降,CPU载荷运算时间也有所缩短,内存占用未见明显改变。
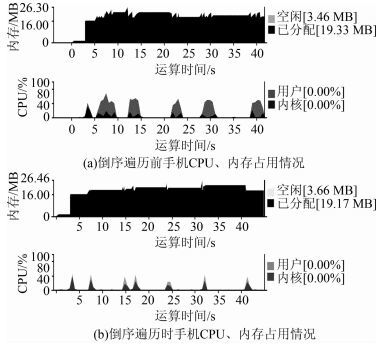 |
| 图 6 倒序遍历前后手机CPU、内存占用情况 Figure 6 CPU, Memory Usage Before and After Reverse Traversal |
表 2为通过监测软件获得的具体提升数据。由表 2可知, 通过此方法进行优化处理,CPU占用峰值下降42.56%,CPU载荷运算时间下降37.74%,优化效果显著。
| 表 2 倒序遍历前后数据对比 Table 2 Data Comparison Before and After Reverse Traversal |
 |
3 静态室内地图路径规划算法实现
为了验证改进的A-Star算法在静态室内地图路径规划应用中的可用性,开发了一款基于智能手机平台的APP,界面部分截图和功能介绍如图 7所示。APP主要功能包括:通过搜索框对目标地的搜索,扫描二维码获取当前位置信息,使用本文提出的改进的A-Star算法进行室内地图的路径规划,使用指南针辅助用户确定当前朝向等。
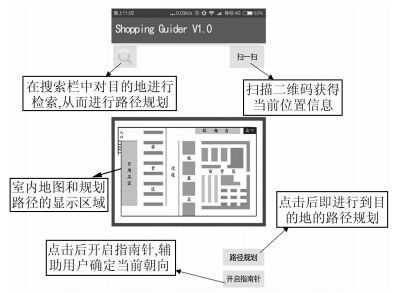 |
| 图 7 APP部分界面展示 Figure 7 Display of APP Interface |
图 8为室内路径规划示例界面。用户通过屏幕点击或者扫描预设的二维码识别当前位置信息,再通过搜索按钮获取目标位置信息,APP即可进行从当前位置到目标位置的路径规划并显示出来。在整个路径规划过程中,当用户不能确定当前方向时,可开启指南针功能键,辅助确定当前朝向。路径规划功能测试表明,CPU占用峰值为42.4%,CPU载荷运算时间为2.7 s,内存占用为17.44 MB,从开始规划路径到显示路径所用时间为3.9 s。这说明改进的A-Star算法在静态室内地图路径规划中的应用是可行的,且运算速率快。
 |
| 图 8 室内地图路径规划示例 Figure 8 Example of Indoor Map Path Planning |
4 结束语
本文针对目前主流静态路径规划算法运算效率较低、对复杂拓扑地形适用性差的缺点,提出将人工智能领域A-Star算法引入静态室内路径规划中的解决方案,并开发出基于智能手机平台的A-Star算法在静态室内地图路径规划应用中的APP软件。技术性验证测试结果表明,依据此方案得到的静态室内路径规划具有与室内地图结合性好、运算速率快、存储效率高等优点。
| [1] | Huang R, Zaruba G V. Static Path Planning for Mobile Beacons to Localize Sensor Networks[C].The 5th Annual IEEE International Conference on Pervasive Computing and Communications Workshops, White Plains, NY, USA, 2007 |
| [2] | Zhan F B, Noon C E. Shortest Path Algorithms: An Evaluation Using Real Road Networks[J]. Transportation Science, 1998, 32(1): 65–73 DOI: 10.1287/trsc.32.1.65 |
| [3] | Hougardy S. The Floyd-Warshall Algorithm on Graphs with Negative Cycles[J]. Information Processing Letters, 2010, 110(8): 279–281 |
| [4] | Wang K H C, Botea A. Tractable Multi-Agent Path Planning on Grid Maps[C]. The 21st International Joint Conference on Artificial Intelligence, Pasadena, California, USA, 2009 |
| [5] | Altaharwa I A, Alweshah M. A Mobile Robot Path Planning Using Genetic Algorithm in Static Environment[J]. Journal of Computer Science, 2008, 4(4): 341–344 DOI: 10.3844/jcssp.2008.341.344 |
| [6] | 徐伟, 孙士兵. 基于A-Star算法警用地图查询系统的设计与实现[J]. 信息安全与技术, 2011, (5): 52–53 |
| [7] | 魏瑞轩, 许卓凡, 王树磊, 等. 基于Laguerre图的自优化A-Star无人机航路规划算法[J]. 系统工程与电子技术, 2015, 37(3): 577–582 |
| [8] | 陈圣群, 董林飞. Dijkstra和A-Star算法在智能导航中的应用分析[J]. 重庆科技学院学报·自然科学版, 2010, 12(6): 159–161 |
| [9] | 李季, 孙秀霞. 基于改进A-Star算法的无人机航迹规划算法研究[J]. 兵工学报, 2008, 29(7): 788–792 |
| [10] | 陈华华, 杜歆, 顾伟康. 基于遗传算法的静态环境全局路径规划[J]. 浙江大学学报(理学版), 2005, 32(1): 49–53 |
| [11] | Zou H, Zong L, Liu H, et al. Optimized Application and Practice of A* Algorithm in Game Map Path-Finding[C].IEEE International Conference on Computer and Information Technology, Bradford, West Yorkshire, UK, 2010 |
| [12] | 周建国, 张鹏, 冯欣, 等. 基于无线传感器网络的室内定位研究[J]. 测绘地理信息, 2012, 37(5): 26–28 |
 2017, Vol. 42
2017, Vol. 42

