| 线路曲线的测设 |
为满足国民经济建设的需要,很多高校都开设了工程测量这一学科,为国家现代化事业的建设培育大量的骨干技术人员[1]。然而,学校教学所用的2015年武汉大学出版的《工程测量学》中,曲线测设部分所引用的公式精度已无法满足现代化线路精度的要求。尤其在缓和曲线部分,其所用公式在离直缓点250 m曲线长的情况下,计算出的线路坐标误差已接近1 cm,因而,其应用范围受到极大限制,有必要对其中的线路中边桩坐标计算模型和计算精度进行深入研究。本文就曲线测设方面总结出了一套详细的曲线测设理论。
1 线路的分类线路工程通常是由直线和曲线组成,曲线又分为圆曲线、缓和曲线、复曲线和竖曲线等[2]。圆曲线分单圆曲线和复曲线两种。单圆曲线是具有单一半径的曲线,复曲线是具有两个或两个以上不同半径的曲线。线路平面常见的线性有直线、圆曲线和缓和曲线3种类型。其中,直线-第一缓和曲线-圆曲线-第二缓和曲线-直线是铁路线路的基本组合线形[3], 见图 1。
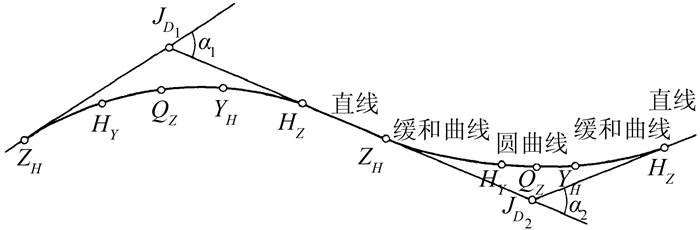 |
| 图 1 铁路线路示意图 Figure 1 Schematic Diagram of the Railway Line |
缓和曲线的设计一般不宜过长。不合理的缓和曲线长度会影响驾驶行为和交通安全。法国设计规范建议修改缓和曲线设计,显著减小缓和曲线长度,但同时认为缓和曲线长度尚有待进一步分析。意大利学者曾在双车道公路上进行的行驶轨迹及驾驶行为的调查表明,过长的缓和曲线确实对驾驶行为有负影响,特别是在需要减速的曲线上[4]。
2 曲线要素 2.1 曲线综合要素计算及主点测设如图 2所示,已知圆曲线的半径为R,两端缓和曲线长为l0,曲线转向角为α,曲线要素为:
| $ \left\{ \begin{array}{l} T = \frac{{{l_0}}}{2} - \frac{{l_0^3}}{{240{R^2}}} + \left( {R + \frac{{l_0^2}}{{24R}}} \right){\rm{tan}}\frac{\alpha }{2}T = \\ \;\;\;\;R{\rm{tan}}\frac{\alpha }{2};L = \frac{{R\alpha \pi }}{{180^\circ }} + {l_0};{E_0} = \\ \;\;\;\;\left( {R + \frac{{{l_0}^2}}{{24R}}} \right)\sec \frac{\alpha }{2} - R;q = 2T - L \end{array} \right. $ | (1) |
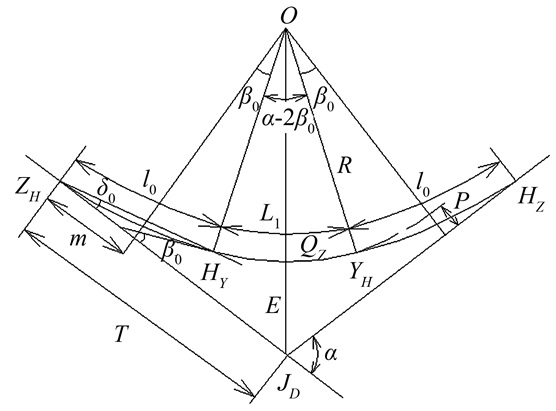 |
| 图 2 线路各要素示意图 Figure 2 Circuit Schematic Diagram of the Elements |
式中, T为切线长;L为曲线长;E0为外矢距;q为切曲差;它们与R、α、l0一起称为曲线综合要素。图 2中,ZH(直缓点)、HY(缓圆点)、QZ(曲中点)、YH(圆缓点)和HZ(缓直点)称为带有缓和曲线的圆曲线的主点,m为切垂距,P为圆曲线内移值,β0为缓和曲线的切线角,m、P、β0为:
| $ m = \frac{{{l_0}}}{2} - \frac{{l_0^3}}{{240{R^2}}};P = \frac{{l_0^2}}{{24R}};{\beta _0} = \frac{{{l_0}}}{{2R}}\frac{{180^\circ }}{\pi } $ | (2) |
直缓点里程为:LZH=LJD-T,其中,LJD为交点里程; 缓圆点里程为:LHY=LZH+l0; 曲中点里程为:
曲线上任一点i的曲率半径与该点至起点的曲线长成正比,即Ri∝1/li或Ri=C/li,其中,C为缓和曲线半径的变更率[4]。在缓圆点或直缓点处,Ri=R,则C=Rl0。如图 3所示,β为过点i的切线与X轴的夹角为:
| $ \beta = \frac{{l_i^2}}{{2R{l_0}}} \cdot \frac{{180^\circ }}{\pi } $ | (3) |
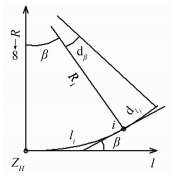 |
| 图 3 缓和曲线上切线倾角 Figure 3 Tangent Inclination on Transition Curve |
如图 4所示,可推算出未知点i在点ZH切线坐标系上的坐标为:
| $ x = {l_i} - \frac{{l_i^5}}{{40{R^2}l_0^2}};y = \frac{{l_i^3}}{{6R{l_0}}} - \frac{{l_i^7}}{{336{R^3}l_0^3}} $ | (4) |
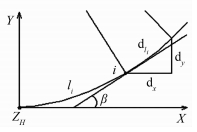 |
| 图 4 切线支距法测设缓和曲线 Figure 4 Transition Curve Surveyed by Tangent Offset Method |
2.3.2 圆曲线部分
设曲线上的点i距点ZH的曲线长为li,由图 5可得点i的坐标公式为[6]:
| $ \left\{ \begin{array}{l} x = R \cdot \sin \left( {\frac{{{l_i} - 0.5{l_0}}}{R} \cdot \rho } \right) + \frac{{{l_0}}}{2} - \frac{{l_0^3}}{{240{R^2}}}\\ y = R\left[ {1 - \cos \left( {\frac{{{l_i} - 0.5{l_0}}}{R} \cdot \rho } \right)} \right] + \frac{{l_0^2}}{{24R}} \end{array} \right. $ | (5) |
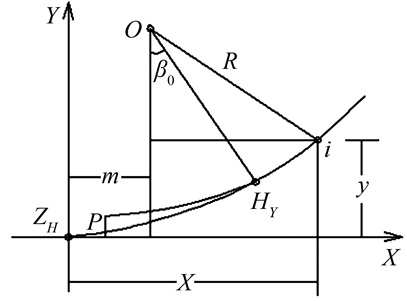 |
| 图 5 切线支距法测设圆曲线 Figure 5 Circular Curve Surveyed by Tangent Offset Method |
式中, ρ=180°/π。
2.4 曲线测设方面的相关因素计算1) 已知曲线长L、缓和曲线长l0、圆曲线半径R,则转向角α为:
| $ \alpha = \frac{{L - {l_0}}}{R} \cdot \frac{{180^\circ }}{\pi } $ | (6) |
由式(6)推算,若已知缓和曲线长l0、圆曲线半径R、转向角α,那么曲线长L为:
| $ L = \alpha R \cdot \frac{\pi }{{180^\circ }} + {l_0} $ | (7) |
2) 已知曲线长L、缓和曲线长l0、圆曲线半径R和直缓点里程LZH,则交点里程为:
| $ \begin{array}{c} {L_{{J_D}}} = {L_{{Z_H}}} + T = {L_{{Z_H}}} + \frac{{{l_0}}}{2} - \frac{{l_0^3}}{{240{R^2}}} + \\ \left( {R + \frac{{l_0^2}}{{24R}}} \right)\tan \left( {\frac{{L - {l_0}}}{R} \cdot \frac{{90^\circ }}{\pi }} \right) \end{array} $ | (8) |
方位角为从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角。在曲线测设的过程中,方位角的运用是非常重要的[7]。当遇到转弯线路时,利用方位角的性质解算出相邻直线的方位角显得尤为方便[8]。如图 6所示,在相邻直线的方位角推算过程中,直线的左右偏情况必须要考虑在内。将直线的左右偏情况用cc表示,cc=-1表示左偏,cc=+1表示右偏,那么当直线右偏时,αBC=αAB+α可转换为:
| $ {\alpha _{BC}} = {\alpha _{AB}} + cc \cdot \alpha $ | (9) |
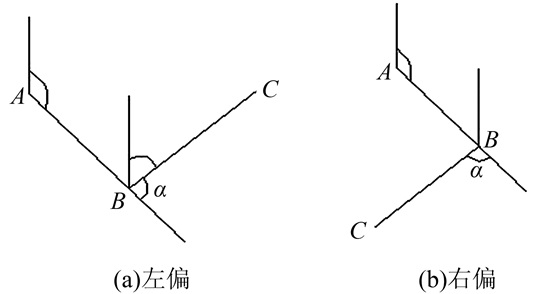 |
| 图 6 相邻直线左右偏线路示意图 Figure 6 Around Partial Schematic Diagram of Adjacent Straight Lines |
方位角的推算在铁路线路坐标的计算过程中运用较多,只有准确解算出相关线路的方位角,才能准确地计算出线路的中边桩坐标[9]。
4 线路的中边桩坐标计算 4.1 中边桩坐标计算设圆曲线的半径为R,两端缓和曲线长为l0,曲线转向角为α,直缓点里程L0以及点i的里程Li,(XJD, YJD)为交点坐标,(X0, Y0)为直缓点坐标,可计算出切线长T、曲线长L、外矢距E0和切曲差q[10],那么缓直点的坐标(X1, Y1)也可求得。
令A0=αZH-JD,A1=αJD-HZ,那么有:
| $ \left\{ \begin{array}{l} {A_1} = {A_0} + cc \cdot \alpha \\ {X_1} = {X_{{J_D}}} + T\cos {A_1};{Y_1} = {Y_{{J_D}}} + T\sin {A_1} \end{array} \right. $ | (10) |
1) 当点i在HZ(上条线路的缓直点)→ZH段上时,有:
| $ \left\{ \begin{array}{l} {l_i} = {L_0} - {L_i},{X_i} = {X_0} + {l_i}\cos ({A_0} + 180^\circ )\\ {Y_i} = {Y_0} + {l_i}\sin ({A_0} + 180^\circ )\\ {X_{左}} = {X_i} + d\cos \left( {{A_0} - 90^\circ } \right)\\ {Y_{左}} = {Y_i} + d\sin \left( {{A_0} - 90^\circ } \right)\\ {X_{右}} = {X_i} + d\cos \left( {{A_0} + 90^\circ } \right)\\ {Y_{右}} = {Y_i} + d\sin \left( {{A_0} + 90^\circ } \right) \end{array} \right. $ | (11) |
式中,li为点i到直缓点的线段长;(Xi, Yi)为点i的坐标;(X左, Y左)、(X右, Y右)分别为与点i对应的左右边桩坐标;d为边桩距。
2) 当点i在ZH→HY段上时,有:
| $ \left\{ \begin{array}{l} {l_i} = {L_i} - {L_0},{x_i} = {l_i} - \frac{{l_i^5}}{{40{R^2}l_0^2}},{y_i} = \frac{{l_i^3}}{{6R{l_0}}} - \frac{{l_i^7}}{{336{R^3}l_0^3}}\\ \beta = \frac{{{l_i}^2}}{{2R{l_0}}}\rho ,\rho = \frac{{180^\circ }}{\pi },{A_i} = {A_0} + cc \cdot \beta ,{X_i} = \\ {X_0} + {x_i}\cos {A_0} - cc \cdot {y_i}\sin {A_0},{Y_i} = {Y_0} + {x_i}\sin {A_0} + \\ cc \cdot {y_i}\cos {A_0},{X_{左}} = {X_i} + d\cos \left( {{A_i} - 90^\circ } \right),{Y_{左}} = \\ {Y_i} + d\sin \left( {{A_i} - 90^\circ } \right),{X_{右}} = {X_i} + d\cos \left( {{A_i} + 90^\circ } \right)\\ {Y_{右}} = {Y_i} + d\sin \left( {{A_i} + 90^\circ } \right) \end{array} \right. $ | (12) |
式中, li为自点ZH起的曲线长;β为点i切线的倾角; Ai为点i切线的方位角; (xi, yi)为按切线支距法求出的点i在ZH点切线坐标系中的坐标; cc为交点到缓直点(JD→HZ)的线路方向相对于直缓点到交点(ZH→JD)线路前进方向的左右偏情况(cc=-1表示左偏,cc=+1表示右偏)。
3) 当点i在HY→YH段上时,有:
| $ \left\{ \begin{array}{l} {l_i} = {L_i} - {L_0}\\ {x_i} = R\sin \left( {\frac{{{l_i} - 0.5{l_0}}}{R} \cdot \rho } \right) + \frac{{{l_0}}}{2} - \frac{{l_0^3}}{{240{R^2}}}\\ {y_i} = R\left[ {1 - \cos \left( {\frac{{{l_i} - 0.5{l_0}}}{R} \cdot \rho } \right)} \right] + \frac{{l_0^2}}{{24R}}\\ \beta = \frac{{{l_i} - 0.5{l_0}}}{R}\rho ,\rho = \frac{{180^\circ }}{\pi },{A_i} = {A_0} + cc \cdot \beta \\ {X_i} = {X_0} + {x_i}\cos {A_0} - cc \cdot {y_i}\sin {A_0}\\ {Y_i} = {Y_0} + {x_i}\sin {A_0} + cc \cdot {y_i}\cos {A_0}\\ {X_{左}} = {X_i} + d\cos \left( {{A_i} - 90^\circ } \right)\\ {Y_{左}} = {Y_i} + d\sin \left( {{A_i} - 90^\circ } \right)\\ {X_{右}} = {X_i} + d\cos \left( {{A_i} + 90^\circ } \right)\\ {Y_{右}} = {Y_i} + d\sin \left( {{A_i} + 90^\circ } \right) \end{array} \right. $ | (13) |
4) 当点i在YH→HZ段上时,有:
| $ \left\{ \begin{array}{l} {l_i} = L - \left( {{L_i} - {L_0}} \right),{A_2} = {A_1} + 180^\circ \\ \beta = \frac{{{l_i}^2}}{{2R{l_0}}}\rho ,\rho = \frac{{180^\circ }}{\pi },cc = - 1 \cdot cc\\ {A_i} = {A_1} + cc \cdot \beta ,{x_i} = {l_i} - \frac{{{l_i}^5}}{{40{R^2}{l_0}^2}}\\ {y_i} = \frac{{{l_i}^3}}{{6R{l_0}}} - \frac{{{l_i}^7}}{{336{R^3}{l_0}^3}}\\ {X_i} = {X_1} + {x_i}\cos {A_2} - cc \cdot {y_i}\sin {A_2}\\ {Y_i} = {Y_1} + {x_i}\sin {A_2} + cc \cdot {y_i}\cos {A_2}\\ {X_{左}} = {X_i} + d\cos \left( {{A_i} - 90^\circ } \right)\\ {Y_{左}} = {Y_i} + d\sin \left( {{A_i} - 90^\circ } \right)\\ {X_{右}} = {X_i} + d\cos \left( {{A_i} + 90^\circ } \right)\\ {Y_{右}} = {Y_i} + d\sin \left( {{A_i} + 90^\circ } \right) \end{array} \right. $ | (14) |
式中, A2=αHZ-JD; li为点i到HZ点的曲线长。
5) 当点i在HZ→ZH(下条线路的直缓点)段上时,有:
| $ \left\{ \begin{array}{l} {l_i} = {L_i} - {L_{{H_Z}}},{X_i} = {X_1} + {l_i}\cos ({A_1}),{Y_i} = \\ {Y_1} + {l_i}\sin ({A_1}),{X_{左}} = {X_i} + d\cos \left( {{A_1} - 90^\circ } \right)\\ {Y_{左}} = {Y_i} + d\sin \left( {{A_1} - 90^\circ } \right)\\ {X_{右}} = {X_i} + d\cos \left( {{A_1} + 90^\circ } \right)\\ {Y_{右}} = {Y_i} + d\sin \left( {{A_1} + 90^\circ } \right) \end{array} \right. $ | (15) |
式中,li为点i到点HZ的线段长。
4.2 与《工程测量学》版相应内容的精度对比分析以上分别在直线-第一缓和曲线-圆曲线-第二缓和曲线-直线等线路不同的位置对点i对应的中边桩坐标解算给予了详细论述,所述的换算公式跟书中所述略有不同,不同之处有以下几点。
1) 缓和曲线上,按切线支距法求出的点i在点ZH切线坐标系中的坐标(xi, yi)略有不同。
《工程测量学》中所述公式为:
| $ {x_i} = {l_i} - \frac{{{l_i}^5}}{{40{R^2}{l_0}^2}},{y_i} = \frac{{{l_i}^3}}{{6R{l_0}}} $ | (16) |
然而,原公式为:
| $ \left\{ \begin{array}{l} {x_i} = \sum\limits_{j = 1}^n {\frac{{{{\left( { - 1} \right)}^{j + 1}}}}{{\left( {2j - 2} \right)!}}} \cdot \frac{1}{{{{\left( {2R{l_0}} \right)}^{2j - 2}}}} \cdot \frac{{{l_p}^{4j - 3}}}{{4j - 3}}\\ {y_i} = \sum\limits_{j = 1}^n {\frac{{{{\left( { - 1} \right)}^{j + 1}}}}{{\left( {2j - 1} \right)!}}} \cdot \frac{1}{{{{\left( {2R{l_0}} \right)}^{2j - 1}}}} \cdot \frac{{{l_p}^{4j - 1}}}{{4j - 1}} \end{array} \right. $ | (17) |
令n=2,则(xi, yi)满足式(4)。显然,书中yi式省掉了
2) 圆曲线上,按切线支距法求出的点i在点ZH切线坐标系中的坐标(xi, yi)略有不同。
本文中按切线支距法得出的(xi, yi)满足式(5),而《工程测量学》中是将式(5)中的
| $ \left\{ \begin{array}{l} {x_i} = {l_i} - \frac{{{{\left( {{l_i} - 0.5{l_0}} \right)}^3}}}{{6{R^2}}} - \frac{{{l_0}^3}}{{240{R^2}}}\\ {y_i} = \frac{{{{\left( {{l_i} - 0.5{l_0}} \right)}^2}}}{{2R}} - \frac{{{{\left( {{l_i} - 0.5{l_0}} \right)}^4}}}{{24{R^3}}} + \frac{{{l_0}^2}}{{24R}} \end{array} \right. $ | (18) |
显然,在此处展开并不方便解算,而且计算出的数值精度也大打折扣。因此,书中换算公式的相对精度依然较低。
3) 求取线路的方位角略有不同。
求取点HZ到点JD的方位角αJD-HZ,《工程测量学》中所用公式为:
| $ {\alpha _{{J_D} - {H_Z}}} = {\alpha _{{Z_H} - {J_D}}} + \alpha $ | (19) |
显然,这种解法是片面的,只有交点到缓直点(JD→HZ)的线路方向相对于直缓点到交点(ZH→JD)线路的前进方向为右偏时,式(19)才成立。同理,书中所求的点JD到点HZ的方位角αHZ-JD的公式αHZ-JD=αZH-JD+α+180°也是存在同样的问题,应该更正为:
| $ {\alpha _{{J_D} - {H_Z}}} = {\alpha _{{Z_H} - {J_D}}} + cc \cdot \alpha $ |
| $ {\alpha _{{H_Z} - {J_D}}} = {\alpha _{{Z_H} - {J_D}}} + cc \cdot \alpha + 180^\circ $ |
经过与武汉大学出版社出版的《工程测量学》第六章节曲线测设部分内容的对比,书中所讲述的知识虽然简明清晰,然而,其中的细微部分没有给予特殊的强调和备注,部分内容存在一定程度的片面性,其所述公式的换算精度已经不能满足现代化线路的精度要求,容易引起读者的误解和疑惑。
5 结束语通过本文方法与武汉大学出版的《工程测量学》一书中曲线测设内容的对比分析,验证了本文方法的合理性和精确性,其换算精度能够满足现代化线路精度的基本要求。由于涉及的公式繁多,本文中使用分段的方式对不同曲线段的点位中边桩坐标换算进行了详细的论述,以减少该方面的困惑和失误。
| [1] | 邹进贵, 童魁, 朱勇超. GPS控制测量和精密导线在隧道定向中的应用[J]. 测绘地理信息, 2014, 39(2): 42–44 |
| [2] | 张正禄, 李广云, 潘国荣, 等. 工程测量学[M]. 武汉: 武汉大学出版社, 2005 |
| [3] | 贺国宏. 线性计算的通用模型及其在铁道工程中的应用[J]. 铁道学报, 1997, (4): 99–106 |
| [4] | 王福建, 吴国雄, 赛德·M·伊萨. 缓和曲线对交通安全的影响分析[J]. 重庆交通大学学报, 2008, 27(5): 758–762 |
| [5] | 孔凡兵. 新建时速120 km地铁线路曲线超高和缓和曲线长度的研究[J]. 铁道标准设计, 2015, 59(9): 18–21 |
| [6] |
李德光. 铁路线路中线空间坐标与里程换算模型的研究[D]. 成都: 西南交通大学, 2012 http://d.wanfangdata.com.cn/Thesis/Y2106688 |
| [7] |
佘毅. 基于车载近景摄影测量的高速铁路轨道几何状态检测[D]. 成都: 西南交通大学, 2014 http://d.wanfangdata.com.cn/Thesis/Y2575024 |
| [8] | 王俊丰, 花向红. 高铁沉降监测网点稳定性判断指标研究[J]. 测绘地理信息, 2014, 39(6): 39–41 |
| [9] | 梁永. 高速铁路测量建立独立坐标系的数学模型[J]. 铁道工程学报, 2006, 23(7): 34–36 |
| [10] | 赵长石, 韩峰. 铁路中桩坐标统一计算模型[J]. 兰州交通大学学报, 2009, 28(1): 49–51 |
 2017, Vol. 42
2017, Vol. 42

