| 布朗运动模型在露天矿山边坡变形预测的应用 | [PDF全文] |
随着中国的经济高速发展,工程建设项目日益增多,铁路、高速公路、矿山等项目开挖的土体形成的露天陡坡, 由于土石自身重力、水流冲蚀、生产因素等原因,不可避免产生位移变形造成滑坡。据有关统计,中国崩塌、滑坡、泥石流等地质灾害造成的直接经济损失每年达20~30亿元[1]。因此,如何利用监测数据对边坡变形进行有效预测,对滑坡防灾减灾具有重要意义[2]。边坡变形预测可以检验初始设计方案,调整局部施工参数,提高后续设计水平,准确评估施工中边坡自身的稳定性,及时掌握岩土开挖对周边建筑及环境的影响,保证施工过程中的安全[3]。
目前,对边坡变形监测有大量的研究[4-9],边坡变形预测是根据历史变形监测数据对未来变形进行预测,可分为基于数理统计和基于机理模型的两类方法。基于机理模型的方法是根据边坡岩土的形成与变形机理建立预测模型,来预测边坡变形趋势。郑东健等[10]考虑降雨和温度变化的影响,建立了边坡变形的多因素回归时变预测模型;李聪等[1]建立了考虑4种变形机制的边坡稳定预测模型。刘文生等[11]运用对数变换的方法对实测数据进行改进,建立了改进灰色系统预测模型;孙华芬[12]采用插补和奇异值检验方法对监测数据进行了预处理研究,分析了尖山磷矿边坡变形时空演化规律、变形特征和失稳模式;黄永红等[13]利用小波神经网络模型进行了边坡预测研究。目前,基于数理统计的方法未考虑到监测过程中出现的误差。
本文考虑监测数据的误差,采用卡尔曼滤波进行边坡变形的预测,并将其运用于广州某露天矿山边坡监测数据分析与预报中,为该矿山的安全施工提供决策依据。
1 建模原理 1.1 布朗运动模型利用描述边坡变形的数学模型可以预测边坡变形趋势。边坡变形是由山体、基坑、矿山开挖过程或静止状态下,在各种作用力下,如震动、雨水冲蚀、自身重力、土石结构改变等,其形状及位置发生的改变。在无塌方的情况下,这些变形可以看作是在作用力情况下随机冲击和累积变形引起的,是随机过程的具体实现。而布朗运动模型能够描述随时间推移,物体受到作用力后受到随机冲击,内部或外部关键参数缓慢变化的情形,基于布朗运动的模型能够满足边坡变形的连续性和增量特性。边坡变形可以表示为:
| $ X(t)=x_{0}+a t+\sigma_{B} B(t) $ | (1) |
式中,X(t)为边坡变形量; x0为t0时刻的变形值;a为漂移系数,代表边坡变形数据变化常量;σB为扩散系数,代表变形数据的波动程度;B(t)为标准布朗运动模型,代表变形过程的随机动态。由于边坡监测点位不同,可设漂移系数a服从正态分布,即a~N(μa, σa2)。
由于监测过程存在误差,需要建立监测数据Y(t)与真实变形数据X(t)之间的关系,在不影响建模的情况下,设Y(t)与X(t)之间的表达式为:
| $ Y(t)=X(t)+\varepsilon(t) $ | (2) |
式中,ε(t)为高斯白噪声,ε(t)~N(0, σε2)。
1.2 参数估计利用监测技术可以获得边坡每个监测点位变形数据,利用极大似然方法对参数向量Θ=(μa, σa, σB, σε)进行估计,记N为监测点数;ti, j为第j个监测点第i次监测时间,其中i=1, 2, …, mj,j=1, 2, …, N,mj为第j个监测点的监测次数;Yn=(Y(tn1), Y(tn2), …, Y(tnmn))T为第n个监测点的监测数据。
由式(1)和式(2),可得:
| $ \boldsymbol{Y}_{n}\left(t_{n j}\right)=a_{n} t_{n j}+\sigma_{B} B\left(t_{n j}\right)+\varepsilon\left(t_{n j}\right) $ | (3) |
设Tn=(tn1, tn2, …, tnmn)T,可以得知Yn服从均值为
得到参数Θ的极大似然估计表达式为:
| $ \begin{array}{*{20}{l}} {L(\theta |\mathit{\pmb{Y}}) = - \frac{{\ln (2{\rm{ \mathsf{ π} }})}}{2}\sum\limits_{n = 1}^N {{m_n}} - \frac{1}{2}\sum\limits_{n = 1}^N {\ln } \left| {{\mathit{\pmb{\Sigma}}_n}} \right| - }\\ {\frac{1}{2}\sum\limits_{n = 1}^N {{{\left( {{{\bf\mathit{\pmb{Y}}}_n} - {\mu _a}{\mathit{\pmb{T}}_n}} \right)}^{\rm{T}}}} \mathit{\pmb{\Sigma}}_n^{ - 1}\left( {{\mathit{\pmb{Y}}_n} - {\mu _a}{\mathit{\pmb{T}}_n}} \right)} \end{array} $ | (4) |
式中,
| $ \;\;\left|{{\mathit{\pmb{\Sigma}}_n}} \right| = \left| {{\mathit{\pmb{\Omega}}_n}} \right|\left( {1 + \sigma _a^2\mathit{\pmb{T}}_n^{\rm{T}}\mathit{\pmb{\Omega}}_n^{ - 1}\mathit{\pmb{T}}} \right) $ | (5) |
| $ \mathit{\pmb{\Sigma}} _n^{ - 1} = \mathit{\pmb{\Omega}} _n^{ - 1} - \frac{{\sigma _a^2}}{{1 + \sigma _a^2\mathit{\pmb{T}}_n^{\rm{T}}\mathit{\pmb{\Omega}} _n^{ - 1}{\mathit{\pmb{T}}_n}}}\mathit{\pmb{\Omega}} _n^{ - 1}{\mathit{\pmb{T}}_n}\mathit{\pmb{T}}_n^{\rm{T}}\mathit{\pmb{\Omega}} _n^{ - 1} $ | (6) |
对式(4)参数μa, σa分别求偏导,得到:
| $ \frac{{\partial L(\theta |\mathit{\pmb{Y}})}}{{\partial {\mu _a}}} = \sum\limits_{n = 1}^N {\mathit{\pmb{T}}_n^{\rm{T}}} \mathit{\pmb{\Sigma}}_n^{ - 1}{\mathit{\pmb{Y}}_n} - {\mu _a}\sum\limits_{n = 1}^N {\mathit{\pmb{T}}_n^{\rm{T}}} \mathit{\pmb{\Sigma}}_n^{ - 1}{\mathit{\pmb{T}}_n} $ | (7) |
| $ \begin{array}{*{20}{l}} {\frac{{\partial L(\theta |\mathit{\pmb{Y}})}}{{\partial {\sigma _a}}} = - \sum\limits_{n = 1}^N {\frac{{{\sigma _a}\mathit{\pmb{T}}_n^{\rm{T}}\mathit{\pmb{\Omega}}_n^{ - 1}{\mathit{\pmb{T}}_n}}}{{1 + \sigma _a^2\mathit{\pmb{T}}_n^{\rm{T}}\mathit{\pmb{\Omega}}_n^{ - 1}{\mathit{\pmb{T}}_n}}}} + }\\ {\sum\limits_{n = 1}^N {{{\left( {{\mathit{\pmb{Y}}_n} - {\mu _a}{\mathit{\pmb{T}}_n}} \right)}^{\rm{T}}}} \mathit{\pmb{\Sigma}}_n^{ - 1}\left( {{\mathit{\pmb{Y}}_n} - {\mu _a}{\mathit{\pmb{T}}_n}} \right)} \end{array} $ | (8) |
通过式(7),可以得到μa的极大似然估计为:
| $ {\hat \mu _a} = \frac{{\sum\limits_{n = 1}^N {\mathit{\pmb{T}}_n^{\rm{T}}} \mathit{\pmb{\Sigma}}_n^{ - 1}{\mathit{\pmb{Y}}_n}}}{{\sum\limits_{n = 1}^N {\mathit{\pmb{T}}_n^{\rm{T}}} \mathit{\pmb{\Sigma}}_n^{ - 1}{\mathit{\pmb{T}}_n}}} $ | (9) |
将式(9)带入式(8),得到参数b, σa, σε, σB的极大似然表达式为:
| $ \begin{array}{*{20}{l}} & L\left( {{\sigma }_{a}}, {{\sigma }_{B}}, {{\sigma }_{\epsilon }}, b|\mathit{\pmb{Y}}, {{{\hat{\mu }}}_{a}} \right)=\frac{1}{2}\ln (2\text{ }\!\!\pi\!\!\text{ })\sum\limits_{n=1}^{N}{{{m}_{n}}}- \\ & \;\;\;\;\frac{1}{2}\sum\limits_{n=1}^{N}{\ln }\left| {{\mathit{\pmb{\Sigma}}}_{n}} \right|-\frac{1}{2}\sum\limits_{n=1}^{N}{\mathit{\pmb{Y}}_{n}^{\text{T}}}\mathit{\pmb{\Omega}}_{n}^{-1}{{\mathit{\pmb{Y}}}_{n}}+ \\ &\;\;\;\;\;\;\;\; \frac{\sum\limits_{n=1}^{N}{\mathit{\pmb{T}}_{n}^{\text{T}}}\mathit{\pmb{\Sigma}}_{n}^{-1}{{\mathit{\pmb{Y}}}_{n}}}{\sum\limits_{n=1}^{N}{\mathit{\pmb{T}}_{n}^{\text{T}}}\mathit{\pmb{\Sigma}}_{n}^{-1}{{\mathit{\pmb{T}}}_{n}}}\sum\limits_{n=1}^{N}{|}\mathit{\pmb{T}}_{n}^{\text{T}}\mathit{\pmb{\Sigma}}_{n}^{-1}{{\mathit{\pmb{Y}}}_{n}}- \\ &\;\;\;\; \frac{1}{2}{{\left[ \frac{\sum\limits_{n=1}^{N}{\mathit{\pmb{T}}_{n}^{\text{T}}}\mathit{\pmb{\Sigma}}_{n}^{-1}{{\mathit{\pmb{Y}}}_{n}}}{\sum\limits_{n=1}^{N}{\mathit{\pmb{T}}_{n}^{\text{T}}}\mathit{\pmb{\Sigma}}_{n}^{-1}{{\mathit{\pmb{T}}}_{n}}} \right]}^{2}}\sum\limits_{n=1}^{N}{\mathit{\pmb{T}}_{n}^{\text{T}}}\mathit{\pmb{\Omega}}_{n}^{-1}{{\mathit{\pmb{T}}}_{n}} \\ \end{array} $ | (10) |
通过极大化式(10)可得到参数估计值。
1.3 边坡变形预测为利用卡尔曼滤波对参数及真实变形值X(t)的进行更新预测,需要建立合适的状态空间模型,对式(1)和式(2)离散化,可得
| $ \left\{\begin{array}{l}{X_{k}=X_{k-1}+a_{k} t_{k}-a_{k-1} t_{k}+W_{k-1}} \\ {Y_{k}=X_{k}+\varepsilon_{k}}\end{array}\right. $ | (11) |
式中,Xk=X(tk);Yk=Y(tk)。为简化计算,设Wk和εk为相互独立的随机变量,由布朗运动的特性可知,Wk~N(0, σB2×Δtk), εk~N(0, σε2)。
为方便更新参数ak及Xk,可将ak设为随机变动的参数,即:
| $ a_{k}=a_{k-1}+W_{a k} $ | (12) |
式中, Wak为服从N(0, σa2)的正态分布。由此可将ak及Xk设置为新的状态变量,即
| $ \left\{\begin{array}{l}{\boldsymbol{X}_{k}^{\Delta}=\boldsymbol{A} \boldsymbol{X}_{k-1}^{\Delta}+\boldsymbol{W}_{k-1}^{\Delta}} \\ {Y_{k}=\boldsymbol{H} \boldsymbol{X}_{k}^{\Delta}+\varepsilon_{k}}\end{array}\right. $ | (13) |
式中,
利用卡尔曼滤波方法步骤如下:
1) 初始化
| $ \left\{\begin{array}{l}{\hat{\boldsymbol{X}}_{0}^{\Delta}=\boldsymbol{E}\left(\boldsymbol{X}_{0}^{\Delta}\right)} \\ {\boldsymbol{P}_{0}=\boldsymbol{E}\left[\left(\boldsymbol{X}_{0}^{\Delta}-\hat{\boldsymbol{X}}_{0}^{\Delta}\right)\left(\boldsymbol{X}_{0}^{\Delta}-\hat{\boldsymbol{X}}_{0}^{\Delta}\right)\right]}\end{array}\right. $ | (14) |
2) tk时刻状态估计:
| $ \left\{\begin{array}{l}{\boldsymbol{P}_{k}^{-}=\boldsymbol{P}_{k-1}+\mathit{\pmb{\Sigma}}} \\ {\boldsymbol{K}=\Delta t_{k}^{2} \boldsymbol{P}_{k}^{-}+\sigma_{\varepsilon}^{2}} \\ {\hat{\boldsymbol{X}}_{k}^{\Delta}=\hat{\boldsymbol{X}}_{k-1}^{\Delta}+\boldsymbol{P}_{k}^{-} \boldsymbol{K}_{k}^{-1}\left(Y_{k}-Y_{k-1}-\hat{\boldsymbol{X}}_{k-1}^{\Delta} \times \Delta t_{k}\right)}\end{array}\right. $ | (15) |
3) 更新方差为:
| $ \boldsymbol{P}_{k}=\boldsymbol{P}_{k}^{-}-\boldsymbol{P}_{k}^{-} \Delta t_{k}^{2} \boldsymbol{K}_{k}^{-1} \boldsymbol{P}_{k}^{-} $ | (16) |
式中, Σ=cov(W, Wa)。
通过卡尔曼滤波及参数更新,即可获得真实变形值在tk时刻的估计值为:
| $ X_{k}, \text { i. e. } X_{k} | \boldsymbol{Y}_{1 ; k} \sim N\left(\hat{X}_{k}, \hat{P}_{k}\right) $ | (17) |
式中,Y1:k为直到tk时刻的观测数据, 1:k为1, 2, 3, …, k。
利用监测数据Y1:k,通过卡尔曼滤波可以得到变形一步预测值为:
| $ \hat{X}_{k+1}=\hat{X}_{k}+\hat{a}_{k}\left(t_{k+1}-t_{k}\right) $ | (18) |
越堡水泥矿山位于广州市北部,属于花都区炭步镇乌茶布矿区青龙岗矿段的石灰石矿,是具有代表性的凹陷露天矿。
该矿区位于平原和丘陵的交接处,即河流阶地平原和低山丘陵。由于矿区内池塘的分布相对密集,所以用于排水灌溉的沟渠纵横交错,且区内平原处大多分布着鱼塘,因此稻田所占面积相对较少。距离矿区一定距离外存在河流。有5 km外的巴江河、矿区以南7 km处流淌的芦苞河以及距矿区外围南部8 km的官窑涌,从北西方向向东南方向流动最终注入珠江。由于河流的存在,即受到潮汐的影响。涨潮时,由于密度不同,河水在上,使得在顶托作用的影响下出现倒流现象,导致河水水位升高,影响矿山边坡。矿山经过近20年来的露天开采,目前采空区形成深凹陷的椭圆形深坑。多个大面积的水坑及池塘邻近采空区北边入口。周边边坡高差因不断开采而加大,积水坑水在雨季时会向采空区渗透。图 1为矿区边坡影像,红色方框标注为需要监测的边坡区域。
 |
| 图 1 矿区边坡影像图 Fig.1 Image of Mine Slope |
利用近景摄影测量技术对边坡测点位移数据进行监测,根据选点要求建立6座工作基点,确定监测范围,垂直于边坡走向方向布置测线(沿滑体中央部位向两侧分布、工程地质条件复杂及受地表水危害大处),在测线或其两侧5 m范围内地质、地貌特征点位置设立测点13个测点。根据变形情况及工程进展而定,在6个月内总共监测12次,每月进行两次观测。采用Agisoft Photo Scan 3D扫描软件对图形进行处理并计算出监控点位移量,得到12期变形监测数据,这里给出第一期和第二期监测点变形3D比较图,如图 2所示。
 |
| 图 2 第一期与第二期监测数据3D比较 Fig.2 Comparison of Phase Ⅰand Ⅱ3D Monitoring Data |
监测初始共设立13个监测点,但在进行第一期数据观测后,边坡在治理导致3个测点被施工的土石方掩埋,故开始只有10个测点监测数据;因为10月底边坡治理,测点JC321被掩埋,所以11月份两次监测数据只有9个测点。监测点JC321变形程度较大,能够代表变形的典型特征,同时对典型监测点JC321的水平位移进行预测,来验证本文方法的有效性。
2.2 预测结果利用均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)对预测结果进行评价:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathop{\rm RMSE}\nolimits} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{\hat X}_i} - {Y_i}} \right)}^2}} } }\\ {{\mathop{\rm MAPE}\nolimits} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat X}_i} - {Y_i}}}{{{Y_i}}} \times 100\% } \right|} } \end{array}} \right. $ | (19) |
式中,Yi为第i个实际测量值;
测点JC231的水平位移预测结果如图 3所示。
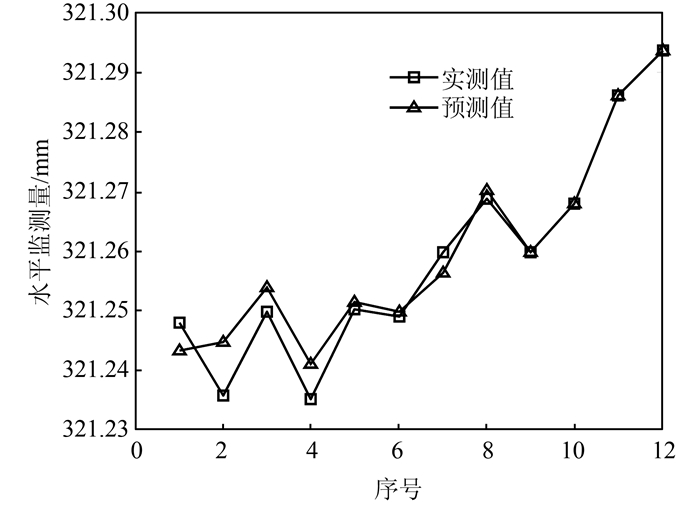 |
| 图 3 监测点JC321水平位移预测结果 Fig.3 Horizontal Displacements Predition of Monitoring Point JC321 |
监测时间点1、6、12处预测值的MAPE分别为0.031%、0.028%、0.017%。
由图 3可知:①基于布朗运动模型的预测方法能够较为迅速地跟踪边坡变形趋势,且随着监测数值的增加,预测精度也随之提高;②监测点JC231水平位移预测的误差结果为RMSE=0.021,MAPE=0.017%,一般来说在变形预测中,变形监测的误差小于8%即可[14],表明本文提出的基于布朗运动模型的预测方法可以较为准确地预测出边坡变形;③从预测误差来看,通过卡尔曼一步预测方法对边坡变形预测,由于动态更新较快,对模型参数的估计较为准确,所以变形预测效果较好,总体误差较小;④边坡变形在第8期~12期后呈明显上升趋势,表明后续需要加大监测力度,防止滑坡灾害发生。
3 结束语布朗运动的预测模型是基于历史监测数据对未来的变形进行预测,根据卡尔曼滤波特性,预测误差会随着监测数据的增多而减小,从结果也可以看出,随着历史监测数据的增多,变形预测精度也越来越高。利用卡尔曼一步预测准确度较高,但对于多步预测是否能够保持预测精度,需要下一步深入研究。
| [1] |
李聪, 姜清辉, 周创兵, 等. 考虑变形机制的边坡稳定预测模型[J]. 岩土力学, 2011, 32(S1): 545-550. |
| [2] |
霍成胜, 王成栋, 孟军海, 等. 基于灰色时序组合模型的基坑监测预测[J]. 黄金科学技术, 2014, 22(5): 79-83. |
| [3] |
刘艳. 深基坑检测技术及进展[J]. 山西建筑, 2007, 33(32): 117-118. DOI:10.3969/j.issn.1009-6825.2007.32.073 |
| [4] |
宋立明, 章传银, 秘金钟, 等. 基于GPS的近景测量定位方法研究[J]. 测绘科学, 2011, 36(2): 40-41. |
| [5] |
李曙锋, 贺跃光. 露天矿山边坡变形监测及工程实例[J]. 江西有色金属, 2002, 16(2): 1-4. DOI:10.3969/j.issn.1674-9669.2002.02.001 |
| [6] |
周丽静, 卢才武, 顾清华, 等. 基于北斗系统的露天矿边坡位移监测系统研究[J]. 自动化与仪表, 2015, 30(4): 35-38. DOI:10.3969/j.issn.1001-9944.2015.04.009 |
| [7] |
胡大治, 蒋勇. 露天矿滑坡的原因和防治[J]. 西部探矿工程, 2015, 27(4): 7-8. DOI:10.3969/j.issn.1004-5716.2015.04.003 |
| [8] |
周明, 邱凌云. 高危边坡变形监测与预警系统研究[J]. 测绘地理信息, 2018, 43(3): 48-50. |
| [9] |
许文学, 羊远新, 李锋, 等. GPS配合全站仪在机场边坡变形监测中的应用[J]. 测绘地理信息, 2012, 37(6): 60-63. |
| [10] |
郑东健, 顾冲时, 吴中如. 边坡变形的多因素时变预测模型[J]. 岩石力学与工程学报, 2005, 24(17): 3180-3184. DOI:10.3321/j.issn:1000-6915.2005.17.028 |
| [11] |
刘文生, 张燕凤, 张贺然, 等. 灰色系统模型在露天矿边坡沉降预测中的应用[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(12): 1608-1612. |
| [12] |
孙华芬.尖山磷矿边坡监测及预测预报研究[D].昆明: 昆明理工大学, 2014
|
| [13] |
黄永红, 徐勇. 基于小波神经网络的某边坡预测研究[J]. 测绘工程, 2012, 21(2): 61-63. DOI:10.3969/j.issn.1006-7949.2012.02.017 |
| [14] |
刘贺, 张弘强, 刘斌. 基于粒子群优化神经网络算法的深基坑变形预测方法[J]. 吉林大学学报(地球科学版), 2014, 44(5): 1609-1614. |
 2019, Vol. 44
2019, Vol. 44

