| BDS-3新卫星对BDS-2短基线相对定位精度的影响分析 |
北斗卫星导航系统(BeiDou navigation satellite- system, BDS)简称北斗系统, 是根据我国基本国情自主设计建设的卫星导航系统, 是我国重要的空间基础设施[1-3]。北斗系统建设与服务能力的不断完善, 不仅丰富了全球导航与定位方式的多样性, 也为全球的发展与建设增添了新活力[4-8]。根据北斗系统的发展战略, 北斗系统已经完成北斗二号(BDS-2)的建设, 目前正处于北斗三号(BDS-3)的建设, 预计完整的北斗系统于2020年建设完成[9-11]。截至2018年底, 我国共发射19颗BDS-3卫星, 其中18颗中高轨道卫星(medium earth orbit, MEO)和1颗地球静止轨道卫星(geostationary earth orbit, GEO)。BDS-3新卫星保留了BDS-2卫星B1I和B3I信号频率, 同时增加了B1c、B2a和B2b这3个新频率, 其中B2b频率与BDS-2卫星B2I频率一致, 但调制类型不同。BDS-3是在BDS-1、BDS-2基础上发展起来的, 经过一些专家研究发现: BDS-3新卫星的多径效应有明显减弱, 在未来将提供更为全方位的服务, 除基本导航、通信服务外, 还将在星基增强、精密单点定位、国际搜救等方面提供全球的服务[12]。此外, 在BDS-3新卫星上搭载了新的国产氢原子钟, 新的国产原子钟比BDS-2与BDS-1上搭载的原子钟更加稳定, 经部分学者研究发现BDS-3新卫星C31和C32与GPS基本一致, 相比于BDS-2有了较大提升。而对于BDS-3新卫星的数据质量以及定位性能进行了初步评估, 宋倩等[13]分析了BDS-3伪距测量误差特性, 发现BDS-3新卫星伪距多路径误差有了较为明显的改善, 最大值在±1 m左右变化, 与GPS卫星特性类似; 程军龙等[14]对BDS-3新卫星的数据质量以及定位性能进行了初步评估, 发现BDS-3新卫星的信噪比除B1I频率高于BDS-2卫星之外, 其他基本一致, BDS-3新卫星中不存在BDS-2卫星中的系统偏差, BDS-3新卫星的加入, 有效的改善了BDS卫星几何分布结构, 提升了伪距单点定位与短基线相对定位精度; 李国梁等[15]分析了BDS-3标准单点定位精度, 发现在观测区域内, BDS-3的数据质量较好, 单系统定位精度优于BDS-2的定位精度; 尹志豪等[16]分析了BDS-3数据质量, 发现BDS-3卫星的信噪比优于BDS-2卫星信噪比, 兼容频率的信噪比也比GPS和Galileo高1~2 dB-Hz, BDS-3卫星的B1C多路径误差大于GPS, 信噪比高于Galileo, 低于GPS, BDS-3的数据饱满度与连续性优于GPS和Galileo。
为进一步分析BDS-3新卫星对BDS-2定位精度的影响, 本文基于2019年1月1日的IGS(Interna- tional GNSS Service)连续跟踪站实测数据, 评估了BDS-3新卫星与BDS-2卫星相同频率(B1I、B3I、B2I/B2b)的数据质量, 分析了BDS-3新卫星对BDS -2卫星的B1I、B2I/B2b以及B3I不同组合频率短基线相对定位精度的影响。
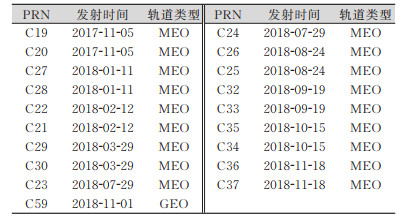
1 BDS-3新卫星简介我国在发射BDS-3之前, 在2015年与2016年先后试验了5颗BDS-3卫星, 2017年11月5日才发射第一颗BDS-3正式卫星, 这标志着我国正式进入BDS-3阶段的建设, 2018年是我国BDS-3建设最快的一年, 先后共发射了19颗卫星, 其卫星基本情况如表 1所示。
| 表 1 BDS‐3卫星一览表 Tab.1 List of BDS-3 |
 |
2 BDS-3数据质量评估
北斗定位的可靠性与准确性很大程度上取决于北斗的数据质量, 因此在进行数据处理之前进行数据质量评估是十分必要的。本文主要评估了BDS-2和BDS-3的信噪比以及多路径均方根值(root mean square, RMS)情况。
2.1 信噪比信噪比是卫星发射信号强度与观测噪声的比值, 是反应信号强度的重要指标, 信噪比越高, 证明观测信号强度越高, 反之则越小, 该值可以直接从观测文件中获取。
如图 1所示, B1I频率BDS-2卫星的信噪比主要在43 dB - Hz左右, BDS - 3卫星的信噪比主要在45 dB-Hz左右; B2I/B2b频率BDS-2卫星的信噪比主要在45 dB-Hz左右, BDS-3卫星的信噪比主要在46 dB-Hz左右; B3I频率BDS-2卫星的信噪比主要在45 dB - Hz左右, BDS - 3卫星的信噪比主要在46 dB-Hz左右; 综上发现, B1I频率、B2I/B2b频率以及B3I频率, BDS-2卫星的信噪比整体情况要略低于BDS-3卫星的信噪比。
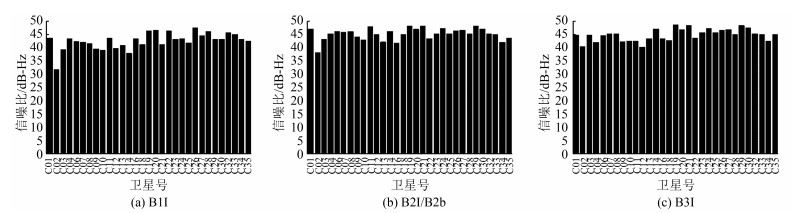 |
| 图 1 BDS‐2与BDS‐3不同频率信噪比 Fig.1 Signal to Noise Ratio of BDS-2 and BDS-3 at Different Frequencies |
2.2 多路径
多路径效应是指接收机天线在接收到卫星直接发射信号与经过地物发射信号叠加所产生的延迟, 是评估GNSS数据质量评估的一项重要指标。
如图 2所示, B1I频率BDS-2各卫星的多路径RMS值主要在0. 47 m左右, BDS-3各卫星的多路径RMS值主要在0. 4 m左右; B2I/B2b频率BDS-2各卫星的多路径RMS值主要在0. 32 m左右, BDS-3各卫星的多路径RMS值主要在0. 25 m左右; B3I频率BDS-2各卫星的多路径RMS值主要在0. 28 m左右, BDS-3各卫星的RMS值主要在0. 3 m左右。综上所述, 在B1I和B2I/B2b两个频率BDS-2卫星的多路径RMS值大于BDS-3卫星的多路径RMS值, 而B3I频率BDS-2多路径RMS值要低于BDS-3多路径RMS值。
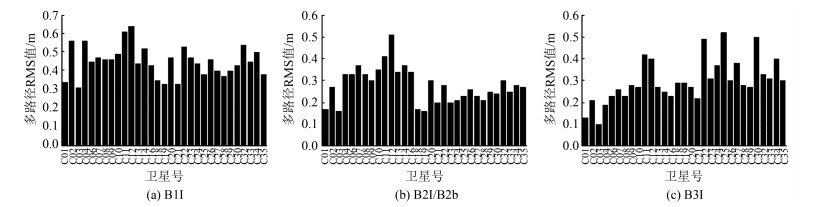 |
| 图 2 BDS‐2与BDS‐3不同频率多路径RMS值 Fig.2 BDS-2 and BDS-3 Multi-path RMS Values at Different Frequencies |
2.3 BDS-3卫星对BDS-2卫星数据质量影响
在分析BDS-3卫星对BDS-2卫星的数据质量影响时, 先分析BDS-2所有卫星各频率的整体平均信噪比与多路径RMS值, 然后加入所有BDS-3卫星的信噪比与多路径RMS值, 再分析加入BDS-3卫星之后所有BDS卫星各频率的整体平均信噪比与多路径RMS值, 通过对比两次的结果, 分析出BDS-3卫星对BDS-2卫星数据质量的影响。
如图 3所示, BDS-3卫星的加入, 使BDS-2每个频率的平均信噪比增加了1 dB-Hz, 使BDS-2卫星B1I频率的多路径RMS值降低了0. 01 m, 使B2I/ B2b频率的多路径RMS值降低了0. 03 m, 使B3I频率的多路径RMS值增加了0. 01 m。
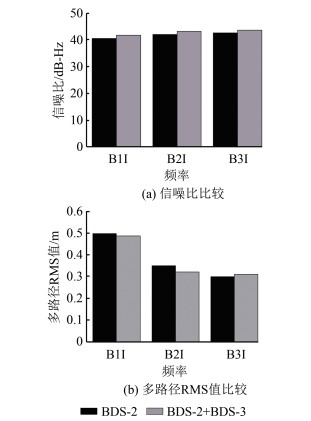 |
| 图 3 BDS‐3卫星对BDS‐2卫星数据质量影响 Fig.3 Impact of BDS⁃3 Satellites on Data Quality of BDS⁃2 Satellites |
3 BDS-3对BDS-2短基线相对定位精度影响
本文选取IGS连续跟踪站的BURZ站与RHPT站, 组成一条4. 28 km的短基线, 观测时间为2019年1月1日与2日共2 d, 数据采样率为30 s, 这两个跟踪站可以同时接收到BDS-2与BDS-3卫星的B1I、B2I/B2b与B3I频率。在进行数据处理时, 首先分析只有BDS-2卫星参与计算的B1I/B2I组合、B1I/B3I组合与B1I/B2I/B3I组合3种组合情况的短基线相对定位三维误差, 由于B2I与B3I组合观测噪声较大, 不适合定位, 因此本文不作分析。然后分析B D S - 3卫星加入的B1I/B2I组合、B1I/B3I组合与B1I/B2I/B3I组合此3种组合情况的短基线相对定位三维误差。
如图 4所示, 第一天的BDS-2短基线B1I/B2I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于16 cm; B1I/B3I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于15 cm; B1I/B2I/B3I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于14 cm。
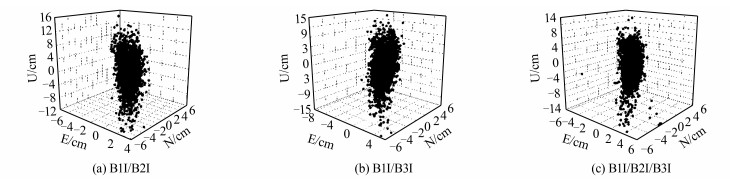 |
| 图 4 第一天BDS‐2短基线相对定位三维误差 Fig.4 Three⁃Dimensional Error of the Relative Positioning of the BDS⁃2 Short Baseline on the First Day |
如图 5所示, 当加入了BDS-3卫星之后, 不同频率组合下的短基线相对定位三维误差有所减小, B1I/B2I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于15 cm; B1I/B3I组合相对定位水平向误差优于6 cm, 竖直方向误差优于12 cm; B1I/ B2I/B3I组合相对定位水平方向误差优于4 cm, 竖直方向误差优于12 cm。由此可以发现, 当BDS-3卫星加入之后, B1I/B2I/B3I组合下短基线相对定位三维误差改善效果最为明显, 而双频组合下竖直方向的误差得到改善的效果最明显。
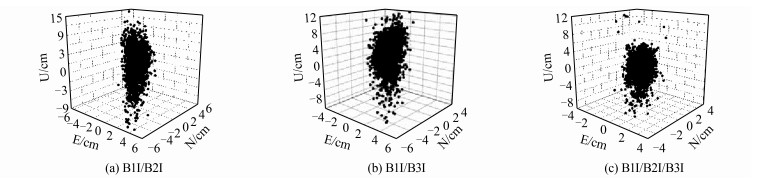 |
| 图 5 第一天BDS‐2/BDS‐3短基线相对定位三维误差 Fig.5 Three⁃Dimensional Error of Relative Positioning of BDS⁃2 / BDS⁃3 Short Baseline on the First Day |
如图 6所示, 第二天的BDS-2短基线B1I/B2I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于12 cm; B1I/B3I组合相对定位水平方向误差优于8 cm, 竖直方向误差优于15 cm; B1I/B2I/B3I组合相对定位E方向误差优于4 cm, N方向误差优于6cm, 竖直方向误差优于11 cm。
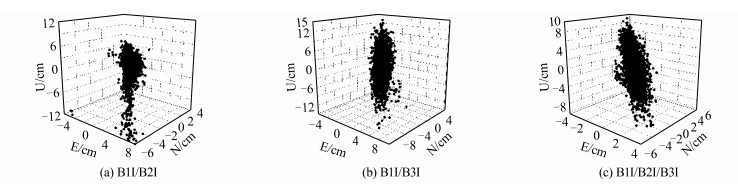 |
| 图 6 第二天BDS‐2短基线相对定位三维误差 Fig.6 Three⁃Dimensional Error of Relative Positioning BDS⁃2 Short Baseline on the Second Day |
如图 7所示, 当加入了BDS-3卫星之后, 不同频率组合下的短基线相对定位三维误差有所减小, B1I/B2I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于12 cm; B1I/B3I组合相对定位水平方向误差优于6 cm, 竖直方向误差优于14 cm; B1I/ B2I/B3I组合相对定位水平方向误差优于4 cm, 竖直方向误差优于8 cm。可以发现, 当BDS-3卫星加入之后, B1I/B2I/B3I组合下短基线相对定位三维误差改善效果最为明显, 而双频组合下竖直方向的误差得到改善的效果最明显。
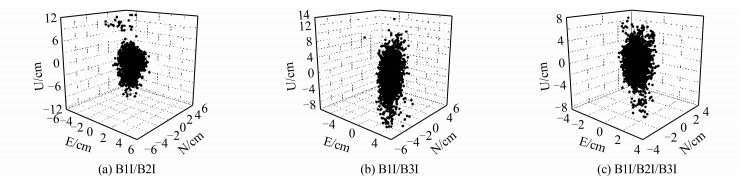 |
| 图 7 第二天BDS‐2/BDS‐3短基线相对定位三维误差 Fig.7 Three⁃Dimensional Error of the Relative Positioning of the BDS⁃2 / BDS⁃3 Short Baseline on the Second Day |
为进一步分析BDS-3卫星对BDS-2短基线相对定位精度的影响, 统计只有BDS-2卫星参与计算时3个方向RMS值以及加入BDS-3卫星参与计算时3个方向RMS值, 结果如表 3所示。
| 表 3 BDS2/BDS‐3短基线相对定位RMS值统计 Tab.3 BDS2/BDS⁃3 Short Baseline Relative Positioning RMS Value Statistics |
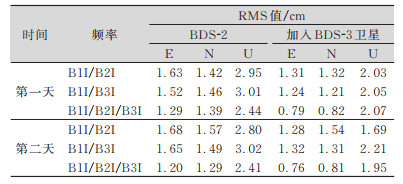 |
由表 3可知, BDS-2不同频率组合下短基线相对定位水平方向RMS值优于2 cm, 竖直方向RMS值优于3 cm, 当加入BDS-3卫星之后, 不同组合水平方向与竖直方向RMS值得到了明显的改善, 其中三频组合下的改善效果最为明显, 水平方向RMS值优于1 cm, 竖直方向RMS值优于2 cm。
4 结束语本文基于IGS连续跟踪站组成的短基线, 分析了BDS-2与BDS-3卫星B1I、B2I/B2b和B3I的数据质量以及BDS-3卫星对BDS-2短基线相对定位精度的影响, 发现:
1) BDS-3卫星整体的信噪比情况优于BDS-2卫星的信噪比, BDS-3卫星的加入使BDS-2卫星B1I、B2I以及B3I平均信噪比增加1 dB-Hz。BDS-3卫星B1I和B2I频率的多路径效应要小于BDS-2卫星的多路径效应, 并且BDS-3新卫星的加入使BDS-2卫星整体的多路径RMS值有所减小, 而BDS-3卫星加入使BDS-2卫星B3I频率的多路径RMS值增加, 原因需进一步分析。
2) 在进行短基线相对定位时, BDS-3卫星的加入使BDS-2短基线相对定位精度有了较明显的提升, 这是因为BDS-3新卫星的加入以及BDS卫星数的增加, 在不同频率组合时, 三频组合时提升效果最为明显, 而竖直方向定位精度的优于水平方向。其中E方向定位精度最大提升39%, N方向最大提升41%, U方向最大提升32%。
本文只分析部分BDS-3卫星对BDS-2相同频率数据质量与短基线相对定位精度的影响, 在我国BDS-3完成建设之后, 需要全面对其定位性能进行分析。
| [1] |
吴明魁, 刘万科, 张小红, 等. BDS-3/GPS/Galileo试验星短基线紧组合相对定位性能初步评估[J]. 武汉大学学报·信息科学版, 2020, 45(1): 13-20. |
| [2] |
田福娟, 聂琳娟, 周晓慧. 基于MGEX数据的北斗PPP精度分析[J]. 测绘地理信息, 2019, 44(2): 74-78. |
| [3] |
赵朋, 花向红, 赵磊磊, 等. 北斗卫星钟差频间偏差及对定位精度影响分析[J]. 测绘地理信息, 2019, 44(1): 27-31. |
| [4] |
张双成, 王倩怡, 刘奇, 等. BDS精密相对定位精度的GAMIT分析[J]. 测绘科学, 2018, 43(12): 92-97. |
| [5] |
张成才, 岳建平. 北斗/GPS组合相对定位及精度分析[J]. 地理空间信息, 2018, 16(8): 30-33. DOI:10.3969/j.issn.1672-4623.2018.08.008 |
| [6] |
刘万科, 胡捷, 曾琪, 等. 基于KinPOS软件的BDS/ GPS动对动相对定位性能分析[J]. 中国惯性技术学报, 2018, 26(4): 428-434. |
| [7] |
苗岳旺, 周巍, 秦文振, 等. 北斗相对定位精度分析[J]. 北京测绘, 2017(S1): 37-39. |
| [8] |
陈健, 岳东杰, 朱少林. BDS/GPS组合单历元相对定位性能分析[J]. 现代测绘, 2017, 40(4): 15-20. DOI:10.3969/j.issn.1672-4097.2017.04.005 |
| [9] |
马文忠, 李林欢, 江丽丽. 基于载波相位差分的北斗/ GPS双模定位系统研究[J]. 测绘工程, 2015, 24(9): 25-30. DOI:10.3969/j.issn.1006-7949.2015.09.006 |
| [10] |
元荣, 白征东, 过静珺. 基于TCCAR的北斗三频相对定位[J]. 大地测量与地球动力学, 2014, 34(4): 106-109. |
| [11] |
白征东, 元荣, 过静珺, 等. 北斗二代卫星厘米级相对定位[J]. 测绘通报, 2014(7): 11-13. |
| [12] |
赵忠海, 张洪文, 马新文. 北斗三号卫星观测数据质量分析[J]. 测绘与空间地理信息, 2019, 42(10): 61-64. |
| [13] |
宋倩, 高皓, 肖胜红, 等. 北斗三号卫星伪距测量误差特征分析[J]. 现代导航, 2019, 10(5): 313-316. DOI:10.3969/j.issn.1674-7976.2019.05.001 |
| [14] |
程军龙, 王旺, 马立烨, 等. 北斗三号观测数据质量及定位精度初步评估[J]. 测绘通报, 2019(8): 1-7. |
| [15] |
李国梁, 钱雨阳. 北斗三号系统标准单点定位精度分析[J]. 全球定位系统, 2019, 44(4): 113-118. |
| [16] |
尹志豪, 王广兴, 胡志刚, 等. 北斗三号观测数据质量分析[J]. 测绘科学, 2019, 44(12): 1-12. |
 2022, Vol. 47
2022, Vol. 47

