| 一种单频RTK周跳探测及处理方法 |
GNSS RTK(real-time kinematic)技术被广泛运用于多个领域,如变形监测、精密农业、自动驾驶等。传统的RTK技术依赖于双频、高精度的接收机,这种接收机成本较高,限制了RTK技术的进一步推广,采用成本较为低廉的单频GNSS接收机实现RTK不失为一种解决方案。但是单频RTK目前还存在一些尚待解决的问题,载波相位观测数据中周跳的探测及处理就是其中之一。
接收机在观测过程中如果发生了卫星遮挡、外界干扰或者接收机高动态等情况,容易发生整周计数的错误,即周跳。周跳具有整数特性;另外,由于引发周跳的因素及其引发的结果难以预测,因此周跳的发生也具有不确定性。
对于多频RTK数据,采用不同频率观测值的线性组合来探测周跳的方法已经十分成熟,如Goad[1]在1985年提出的电离层残差法,Blewitt[2]在1990年提出的TurboEdit方法,GPS现代化后采用三频组合探测周跳[3]等,但是这些方法不适用于单频数据。目前能适用于单频数据周跳探测的方法主要有高次差法、多项式拟合法、多普勒法、观测值残差法等。高次差法由Remondi[4]于1985年提出,主要做法是对载波相位观测值序列在历元间多次求差,通过分析高次差的序列是否出现异常判断是否出现周跳[5]。多项式拟合法采用多项式拟合载波相位观测值的变化,外推出下一个历元的预测观测值并且与实际的观测值进行比较,当两者之差大于阈值的时候认为出现了周跳[6]。上述两种方法均认为在无周跳发生的情况下,载波相位观测值的变化是平稳的。但是当物体运动出现快速变化时,载波相位观测值也将快速变化,高次差法和多项式拟合法无法应对这种变化[7],因此它们的效果将受到影响。在文献[8]中提出的多普勒法,引入多普勒观测值,能够在一定程度上应对物体运动状态变化的情况,但该方法的效果受限于多普勒观测值的精度以及观测采样率。基于几何关系模型的观测值残差法,通过历元间观测值差分求解载体位置,同时得到观测值的残差,通过残差分析判断是否存在周跳[9]。这种方法通过几何模型约束,能够顾及到历元间物体位置的变化对载波相位观测值的影响,在探测周跳方面具有良好的效果,但该方法在确定周跳数值时未充分利用不同卫星观测值残差间的误差相关性。而且,该方法有效性会随着发生周跳卫星数量的增加而下降,当周跳卫星达到可视卫星总数的30%以上时,基于观测值残差处理的周跳探测方法有效性下降至50%以下[10]。
本文提出了一种适用于单频观测值的实时周跳探测和处理方法,将周跳作为模型参数进行估计并确定其整数估值,较好地解决了上述问题。
1 实时周跳探测及处理方法 1.1 观测方程观测方程如下:
| $ \left\{ \begin{array}{l} \Delta \nabla \rho = lX + mY + nZ + L + {\varepsilon _\rho }\\ \Delta \nabla \varphi = lX + mY + nZ - \lambda \Delta \nabla N - \lambda C + L + {\varepsilon _\varphi } \end{array} \right. $ | (1) |
式中,
对于观测值的随机模型,认为非差观测值之间相互独立,因此非差观测值的方差-协方差阵是对角阵,具体数值可依据观测值的精度确定。双差观测值的方差-协方差阵根据非差到双差的转换矩阵,通过方差-协方差传播律得出。
站间单差的转换矩阵为:
| $ \mathop {{\mathit{\boldsymbol{S}}_0}}\limits_{n \times 2n} = \left( {{\rm{ }}\mathit{\boldsymbol{E}}, - \mathit{\boldsymbol{E}}} \right) $ | (2) |
星间单差的转换矩阵为:
| $ \mathop {{\mathit{\boldsymbol{S}}_1}}\limits_{n - 1 \times n} = \left( {{\rm{ }}\mathit{\boldsymbol{E}}, \left( { - 1} \right)} \right) $ | (3) |
双差转换矩阵为:
| $ \mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{S}}_1} \times {\mathit{\boldsymbol{S}}_0} $ | (4) |
若非差观测值的方差-协方差阵为D,则双差观测值的方差-协方差阵为:
| $ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{S}} \times \mathit{\boldsymbol{D}} \times {\mathit{\boldsymbol{S}}^T} $ | (5) |
状态转移方程采用匀速运动模型(理论上也可采用其他运动模型):
| $ \left[ \begin{array}{l} X(k)\\ Y\left( k \right)\\ Z\left( k \right)\\ Vx\left( k \right)\\ Vy\left( k \right)\\ Vz\left( k \right) \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{E}}_{3 \times 3}}}&{{\mathit{\boldsymbol{E}}_{3 \times 3}}}\\ 0&{{\mathit{\boldsymbol{E}}_{3 \times 3}}} \end{array}} \right] \times \left[ \begin{array}{l} X\left( {k - 1} \right)\\ Y\left( {k - 1} \right)\\ Z\left( {k - 1} \right)\\ Vx\left( {k - 1} \right)\\ Vy\left( {k - 1} \right)\\ Vz\left( k \right) \end{array} \right] $ | (6) |
式中,(X, Y, Z)是流动站的三维坐标;(Vx, Vy, Vz)是物体的三维速度;T为历元间的时间间隔;k、k-1分别为历元标志。
本方法认为前后历元间模糊度保持不变,其状态转移方程如下:
| $ N\left( k \right) = N\left( {k - 1} \right) $ | (7) |
周跳的发生具有不确定性,本历元发生的周跳与之前的历元无关,周跳的状态转移方程如下:
| $ C\left( k \right) = 0 $ | (8) |
即认为每个历元周跳的预测值是0。
状态转移方程的随机模型,即前后历元状态转移的过程噪声矩阵(Q)应该与状态转移模型的准确性匹配,模型越不准确,Q就应该越大。通常的动态系统,Q可根据经验或者模拟计算得到,一般取为常值[11-15]。对于模糊度,由于模糊度前后历元应该保持不变,因此模糊度过程噪声(Qnn)取0。对于周跳,由于本历元周跳的值是完全无法预测的,因此对周跳的状态预测是不准确的,周跳参数的过程噪声(Qcc)应该取一个大值。
由卡尔曼滤波的特性可知,滤波结果最终由一步预测值和观测更新值加权而来,即结果受状态转移模型和观测值精度的共同影响。但是流动站的运动状态是不规则且未知的,因此匀速模型预测的状态存在误差,尤其是在流动站急转弯或者剧烈变速的情况下,一步预测误差会对滤波结果有较大的影响,从而影响到周跳探测的结果。为了降低一步预测误差的影响,可以在观测值精度较高的时候,适当的放大位置和速度的过程噪声。
1.3 周跳的解算与处理采用卡尔曼滤波进行参数估计,获得周跳参数的浮点值后,根据周跳值的整数特性,采用LAMBDA方法确定周跳的最优整数值,同时需要对得到的最优整数值进行Ratio检验,检验通过则将该最优整数值作为周跳参数的整数值,否则认为无法确定周跳的整数值。得到周跳的整数值后回代方程重估位置和模糊度,表达式为:
| $ \left\{ \begin{array}{l} {X_{{\rm{fixed}}}} = {X_{{\rm{fixed}}}} - {\mathit{\boldsymbol{D}}_{XC}} \times ({\rm{ }}\mathit{\boldsymbol{D}}_{_{CC}}^{ - 1}) \times ({C_{{\rm{fixed}}}} - {C_{{\rm{fixed}}}})\\ {\mathit{\boldsymbol{D}}_{{X_{{\rm{fixed}}}}}} = {\mathit{\boldsymbol{D}}_{{X_{{\rm{fixed}}}}}} - {\mathit{\boldsymbol{D}}_{XC}} \times \left( {\mathit{\boldsymbol{D}}_{CC}^{ - 1}} \right) \times \mathit{\boldsymbol{D}}_{XC}^T \end{array} \right. $ | (9) |
式中,Xfloat为卡尔曼滤波求解得到的位置和模糊度;Xfixed为整数周跳值回代后解出来的位置和模糊度;DXC为位置、模糊度参数与周跳参数的协方差阵;DCC为周跳参数的方差-协方差阵;Cfloat和Cfixed分别为确定整数值前后的周跳参数;DXfloat和DXfixed分别为回代前后的位置和模糊度方差-协方差阵。
若能确定周跳的整数值且为0,则认为无周跳。若能确定周跳的整数值,且其值不为0,则认为探测出了周跳且可修复,此时将周跳整数值加到整周模糊度参数上,实现周跳的修复:
| $ N\left( k \right) = N\left( {k - 1} \right) + C\left( {k - 1} \right) $ | (10) |
若得到周跳的实数解,无法确认成整数解,则认为探测出周跳但是不可修复。此时重算本历元,同时放大本历元模糊度参数所对应的过程噪声,重估模糊度,表明此时模糊度不再是确定不变的值,存在变化的可能性。过程噪声放大的程度与浮点解的大小成正比。
2 试验 2.1 数据来源采用2018-04-16T15:52:00-16:04:00时间段,司南T300接收机在城市道路环境采集的车载动态GPS+BDS单频数据作为流动站数据,司南M300接收机在武汉大学测绘学院楼顶接收的数据作为基站数据,数据采样率均为1 Hz。
2.2 单颗卫星周跳探测修复有效性检验选取在实验时段参与解算较多的B13号卫星,在观测数据中人为加入各种情况的周跳,输出该时段周跳探测结果。为验证算法对各种类型周跳探测的有效性,加入周跳的种类如表 1~表 3所示。
| 表 1 B13号卫星小周跳加入记录 Tab.1 B13 Satellite Small Cycle Slips Added to the Record |
 |
| 表 2 B13号卫星大周跳加入记录 Tab.2 B13 Satellite Big Cycle Slips Added to the Record |
 |
| 表 3 B13号卫星连续周跳加入记录 Tab.3 B13 Satellite Consecutive Cycle Slips Added to the Record |
 |
 |
| 图 1 B13号卫星原始周跳探测结果 Fig.1 Results of B13 Satellite Original Cycle Slip Detection |
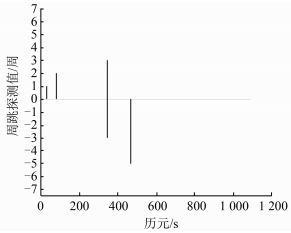 |
| 图 2 B13号卫星小值周跳探测结果 Fig.2 Results of B13 Satellite Small Cycle Slip Detection |
 |
| 图 3 B13号卫星大值周跳探测结果 Fig.3 Results of B13 Satellite Big Cycle Slip Detection |
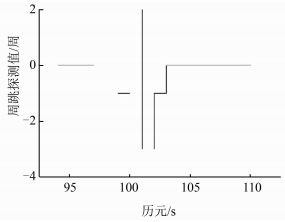 |
| 图 4 连续周跳探测结果 Fig.4 Continuous Cycle Slip Detection Result |
由图 1可知,B13号卫星原始数据仅在第185历元有1周的周跳发生,由图 2和图 3可知,对于发生在B13号卫星的数值各异的大小周跳,都能探测且能确定周跳的准确整数值。图 4显示,连续的周跳同样可以被本算法准确的探测出来。
综上所述,本算法具有对单颗卫星单频动态RTK数据周跳的良好探测和修复能力。
2.3 多卫星周跳探测修复有效性检验选取实验时段数据,每间隔5s对n颗卫星加入m周的周跳,其中n是介于0和共视卫星数减1之间的随机数,m为1~10之间的随机数。本算法对这些周跳的探测情况如表 4所示。
| 表 4 多卫星周跳探测结果 Tab.4 Results of Multiple Satellite Cycle Slip Detection |
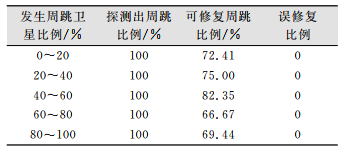 |
在实验中,对于加入周跳的历元:若周跳值被固定成整数值且为0,则认为未探测出周跳;若周跳参数被固定成为正确的整数值则认为探测出周跳且周跳可修复;若周跳值被固定为错误的整数值,则认为周跳修复错误;若周跳未必未被固定成整数值,仅得到实数解,则认为探测出周跳但是周跳不可修复。
由表 4可知,由于对于加入周跳的历元,所有历元周跳值均未被固定成0,因此均认为探测出了周跳,但是仅其中69.44%~82.35%的周跳值被确定为整数,因此仅69.44%~82.35%的周跳能被修复。被确定成整数的周跳值的正确率是100%,并未出现错误固定的情况,因此对于加入周跳的历元并未存在周跳误修复的情况。
基于几何关系的观测值残差法将观测值中的周跳吸收到了观测值的残差中,这给周跳的定位和修复带来了困难,尤其是当多颗卫星出现周跳,则更加难以通过残差分析准确定位多个周跳,从而导致周跳探测失败。而本方法将周跳当作参数估计,再将观测值中的整周误差归化到参数估计值上,获取周跳实数解的同时,能够计算得到不同卫星周跳参数之间的方差-协方差阵。即使多颗卫星同时发生周跳,只要有周跳参数之间准确的相关关系和周跳参数的浮点解,就能利用周跳的整数特性采用LAMBDA方法确定所有周跳参数整数值,实现多颗卫星周跳的准确探测与修复。因此可以从表 4中看出,本算法的周跳探测性能并未明显受到发生周跳卫星数量的影响:对于加入周跳的历元,本算法均能探测出周跳;对于不同的周跳卫星数量,周跳的修复率也没有明显区别。
2.4 动态模式下数据处理实验由于本算法同时估计了位置和周跳,因此在动态环境下若发生周跳,算法的定位性能也是考量指标之一。将本算法的处理结果与RTKLIB 2.4.3的处理结果进行对比,取两者均能得到一定数量固定解的时段作为实验数据段,再在实验数据段中加入周跳,
对于单频数据,RTKLIB 2.4.3采用失锁标识符(Loss of Lock Indicator,LLI)观测值进行周跳的探测和处理,因此加入周跳的同时对数据的LLI值进行的了修改。周跳加入前两者定位结果如图 5所示,其中绿色代表固定解,黄色代表浮点解。
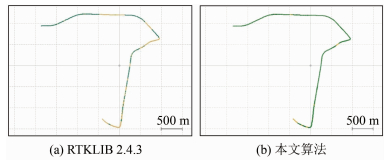 |
| 图 5 原始数据定位结果 Fig.5 Original Data Location Result |
选取两者都固定较好的7:52:00-7:54:00时间段,于7:52:20在B5、B8、B12卫星上分别加入5周、8周、12周的周跳,加入周跳后的结果如图 6所示。
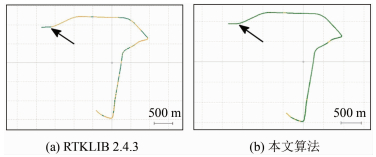 |
| 图 6 加入周跳后定位结果 Fig.6 Adds Cycle Hop to Locate the Result |
加入周跳前后,7:52:00-7:54:00的模糊度固定率如表 5所示。
| 表 5 加入周跳前后模糊度固定率对比/% Tab.5 Blur fixed Rate Before and After Adding Cycle Slip/% |
 |
图 6中箭头所指处即为周跳加入的历元。可见在原始数据均能有较多固定解的前提下,加入周跳后RTKLIB 2.4.3未处理周跳,导致后续历元长时间不可固定,整体数据段的模糊度固定率下降,而本算法的定位结果未受周跳影响。周跳探测最终是为定位服务的,实验证明将周跳作为参数和位置一起估计,在正确处理周跳的同时带来了更好的定位结果。
3 结束语相对于传统的仅采用观测值探测周跳的方法,本文引入了几何关系模型,能够正确地探测单频动态数据的周跳。相对于同样基于几何关系模型的观测值残差法,本文将周跳直接作为参数进行估计,能够使用周跳的方差-协方差阵准确获取周跳值之间的误差相关关系,因此探测效果基本不受周跳卫星数量的影响。同时本算法在探测周跳时能够获取正确的定位结果,不失为一种可用的单频RTK解算方式。此外本算法虽然是基于处理单频数据的周跳提出的,但是对于双频和三频数据同样适用。本文构建的算法的不足之处:其一是状态转移模型的误差会一定程度上影响周跳探测的准确性,有条件可以考虑和惯导器件组合,减少一步预测的误差获得更好的结果;其二是对于未固定的周跳参数无法进行修复,只能重算模糊度,这会对定位结果造成影响,可考虑采取部分获取周跳整数解的方法进行处理,提高周跳的修复率。
| [1] |
Goad C C. Positioning with the Global Positioning System[J]. International Astronomical Union Colloquium, 1980, 56: 191-194. DOI:10.1017/S0252921100081252 |
| [2] |
Blewitt G. An Automatic Editing Algorithm for GPS data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. DOI:10.1029/GL017i003p00199 |
| [3] |
胡云龙, 唐琨, 戴鑫. GPS现代化后的周跳探测方法研究[J]. 测绘地理信息, 2016, 41(1): 14-17. |
| [4] |
Remondi B W. Performing Centimeter-Level Surveys in Seconds with GPS Carrier Phase: Initial Results[J]. Navigation, 1985, 32(4): 386-400. DOI:10.1002/j.2161-4296.1985.tb00918.x |
| [5] |
黄劲松. 高精度GNSS数据处理基本数学模型及算法统一理论研究[D]. 武汉: 武汉大学, 2012
|
| [6] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2009.
|
| [7] |
李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.
|
| [8] |
Cannon M E, Schwarz K P, Wei M, et al. A consistency test of airborne GPS using multiple monitor stations[J]. Bulletin Géodésique, 1992, 66(1): 2-11. |
| [9] |
伍晓勐. 网络RTK基站数据处理关键技术研究[D]. 武汉: 武汉大学, 2016
|
| [10] |
邹璇, 李宗楠, 陈亮, 等. 一种历元间差分单站单频周跳探测与修复方法[J]. 武汉大学学报·信息科学版, 2017(42): 1410-1415. |
| [11] |
吴云. 最优估计与假设检验理论及其在GNSS中的应用[M]. 北京: 科学出版社, 2015.
|
| [12] |
祝文博, 钟红恩, 赵黎平, 等. 航天器伴星长期稳定伴飞姿轨控仿真系统设计[J]. 计算机仿真, 2010(10): 37-39. DOI:10.3969/j.issn.1006-9348.2010.10.010 |
| [13] |
孙玥, 田少雄, 卢山, 等. 椭圆轨道伴飞构型设计与稳定保持[J]. 上海航天, 2016, 33(1): 42-49. DOI:10.3969/j.issn.1006-1630.2016.01.010 |
| [14] |
刘欢, 张柏楠, 张永. 载人航天器与空间站共轨飞行轨道维持策略[J]. 航天器工程, 2019, 28(2): 19-23. DOI:10.3969/j.issn.1673-8748.2019.02.003 |
| [15] |
Gim D W, Alfriend K T. The State Transition Matrix of Relative Motion for the Pert~Bed Noncircular Reference Orbit[J]. Journalof Gnidance, Navigation and Control, 2003, 26(3): 956-971. |
 2021, Vol. 46
2021, Vol. 46

