| GPS RTK解算数据的误差分布研究 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
测量数据处理有以下两个特点:①消除由于多余观测引起的不符值,求解未知量的最优估计;②评定观测值和观测值函数的精度。大多数情况下测量值的概率密度分布是正态的,因此按最小二乘原理处理观测值可以获得最佳估值[1, 2]。对于GPS观测数据,通常认为在经过剔除粗差(整周模糊度)、系统误差改正(电离层、对流层等)后其误差服从正态分布,这有其一定的合理性,但缺乏严格的科学证明。一方面,GPS作为一种新兴的以卫星为载体的测量技术,相对于传统的水准测量、三角测量影响其测量数据精度的因素更是复杂多样;另一方面,虽然科研人员已经找到并建立了相应的模型来处理对流层、电离层延迟等因素的影响,然而由于模型的复杂性或者一些气象参数不能准确得到,系统误差不能完全消除。这些没有完全消除的误差将作为偶然误差对待,有可能对分布产生影响[3]。所以,GPS观测数据经过误差处理后是否服从普遍接受的正态分布需要验证,如果不服从,则讨论其是否服从p-范分布[4-6]。针对此问题,本文采用实际观测的GPS RTK数据进行了相应的实验与检验。
1 统计分布与检验方法 1.1 p-范分布p-范分布的密度函数f(x)和分布函数F(x)分别为[7-9]:
| $ \begin{array}{*{20}{c}} {f\left( x \right) = \frac{1}{{2\beta \mathit{\Gamma }\left( {1/p} \right)}}\exp \left\{ { - {{\left[ {\frac{1}{p} \times \frac{{\left| {x - \mu } \right|}}{\beta }} \right]}^p}} \right\} \cdot }\\ { - \infty < x < + \infty } \end{array} $ | (1) |
| $ F\left( x \right) = \left\{ \begin{array}{l} \int_{ - \infty }^x {f\left( t \right){\rm{d}}t} = \frac{1}{2} + \frac{1}{{2\mathit{\Gamma }\left( {1/p} \right)}}\gamma \left( {\frac{1}{p},z} \right),x \ge 0\\ \int_{ - \infty }^x {f\left( t \right){\rm{d}}t} = \frac{1}{2} - \frac{1}{{2\mathit{\Gamma }\left( {1/p} \right)}}\gamma \left( {\frac{1}{p},z} \right),x < 0 \end{array} \right. $ | (2) |
p-范分布的期望μ和方差D(x)分别为:
| $ \mu = E\left( x \right),{\sigma ^2} = D\left( x \right) = {p^2}{\beta ^2}\frac{{\mathit{\Gamma }\left( {3/p} \right)}}{{\mathit{\Gamma }\left( {1/p} \right)}} $ | (3) |
若用σ2代替式(1)中的参数β,则p-范分布的概率密度函数可写为:
| $ \begin{array}{*{20}{c}} {f\left( x \right) = \frac{p}{{2\sigma \mathit{\Gamma }\left( {1/p} \right)}}{{\left[ {\frac{{\mathit{\Gamma }\left( {3/p} \right)}}{{\mathit{\Gamma }\left( {1/p} \right)}}} \right]}^{\frac{1}{2}}} \times }\\ {\exp \left\{ { - {{\left[ {{{\left[ {\frac{{\mathit{\Gamma }\left( {3/p} \right)}}{{\mathit{\Gamma }\left( {1/p} \right)}}} \right]}^{\frac{1}{2}}}\frac{{\left| {x - \mu } \right|}}{\sigma }} \right]}^p}} \right\}} \end{array} $ | (4) |
从式(4)可以看出,当p=1时,p-范分布就是拉普拉斯分布;当p=2时,p-范分布就是正态分布[10]。当p∈(0, +∞)时,则为p-范分布。
1.2 分布拟合检验皮尔逊χ2检验的原理为:设母总体x的分布函数F(x)未知,其有n个样本观测值x1、x2、…、xn,需在显著性水平α下来检验假设:
| $ {H_0}:F\left( x \right) = {F_0}\left( x \right) \leftrightarrow {H_1}:F\left( x \right) \ne {F_0}\left( x \right) $ | (5) |
其中,F0(x)为某已知分布函数或是某已知类型中的分布函数。
皮尔逊统计量为:
| $ {\chi ^2} = \sum\limits_{i = 1}^k {\frac{{{{\left( {{n_i} - n{p_i}} \right)}^2}}}{{n{p_i}}}} $ | (6) |
当H0为真时,χ2往往比较小,反之较大。皮尔逊还证明:若n充分大(n≥50),则当H0为真时,统计量χ2近似服从χ2(k-1)分布。所以由pH0{χ2≥M}=α可得拒绝域为:
| $ C = \left\{ {{\chi ^2} = \sum\limits_{i = 1}^k {\frac{{{{\left( {{n_i} - n{p_i}} \right)}^2}}}{{n{p_i}}}} \ge \chi _\alpha ^2\left( {k - 1} \right)} \right\} $ | (7) |
而如果在原假设H0中只确定了总体分布的类型,但是分布中还含有m个未知参数,则可由费希尔(Fisher)定理得到,当n很大时,统计量χ2近似服从χ2(k-m-1)分布。此时假设检验的拒绝域为:
| $ C = \left\{ {{\chi ^2} = \sum\limits_{i = 1}^k {\frac{{{{\left( {{n_i} - n{p_i}} \right)}^2}}}{{n{p_i}}}} \ge \chi _\alpha ^2\left( {k - m - 1} \right)} \right\} $ | (8) |
误差的分布是多种多样的,不能期望p-范分布能适合于任何一组观测数据,但是与常用的任何一种分布模式相比,这一分布更灵活,具有更广泛的适应性。对于一组给定的观测值,并不知道p取什么值最为合适。在实际应用中,由于p是p-范分布中的一个参数,可以把p作为未知参数与期望、方差因子一起进行估计,用极大似然法同时估计这3类未知参数的过程在文献[11]中有详细描述,本文直接采用。
2 实例分析 2.1 数据来源本实验采用4种不同的仪器进行数据采集,分别是徕卡1230、华测X90、天宝R8、拓普康,数据采集方式是:将流动站固定,以1 s的采样率进行观测,获取的X、Y、Z坐标值作为检验的样本数据。流动站与基准站的距离小于1 km。因为接收机在一固定位置不动,那么在测量时段内坐标之间的差异可认为是由误差引起的。这里共有8组、4种仪器测量的GPS RTK数据:数据1和数据2:2008-05-28,徕卡1230,分别有952组和736组测量值;数据3和数据4:2011-12-30中午,华测X90,分别有715组和952组测量值;数据5和数据6:2012-12-18,天宝R8,分别有1 343组和1 135组测量值;数据7和数据8:2012-12-26,拓普康,分别有831组和992组测量值。
因为每组测量值都有X、Y、Z 3个坐标分量,可以分别对各个坐标分量进行数据分析,所以实际上可以用来单独处理的数据有24个序列。
2.2 数据预处理为了确保数据的可用性,首先利用拉依达准则把满足
| $ \hat \mu = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} ,\hat \sigma = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \mu } \right)}^2}} } $ | (16) |
再对各数据进行标准化处理(
用皮尔逊χ2检验的方法来检验该组数据是否符合正态分布。检验的原假设为:H0:总体服从正态分布;H1:总体不服从正态分布。
由于数据太多,这里仅列出数据1的X坐标值的检验过程,Y、Z坐标值和其他7组数据检验方法相同。将母体的取值范围划分为20个区间(步长为1 mm),统计各区间内的频数,编程计算得到各区间的概率以及最终χ2统计量的值如表 1所示。
| 表 1 皮尔逊统计量计算过程量统计表 Table 1 Statistical Results of Pearson Statistics |
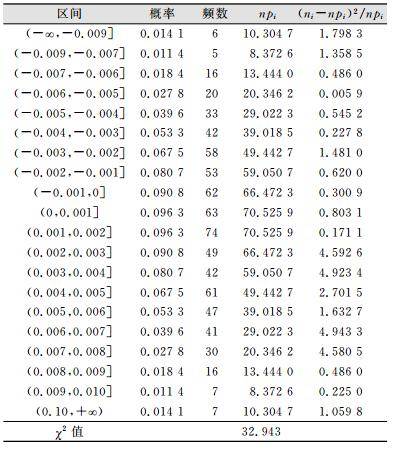 |
对于给定的α=0.05,由于k=20, m=2(在计算χ2前,估计了数学期望
同理,分别对8组数据在X、Y、Z 3个方向上都进行正态分布检验,检验结果为:徕卡1230两组数据在X、Y、Z 3个方向上都不符合正态分布;华测X90、天宝R8两组数据在X、Y、Z 3个方向上都符合正态分布;拓普康两组数据在Y、Z两个方向上都符合正态分布,在X方向上不符合正态分布。
2.4 p-范分布检验由以上分析知,GPS RTK观测数据不完全服从正态分布,为了获得描述RTK观测数据的最佳拟合概率分布密度函数,需要对其进行进一步研究。先对数据1的X、Y、Z 3个坐标方向分别进行检验,其他7组数据的分布检验方法相同。文献[6]已经导出了误差分布的一般模式,本文对其进行p-范分布检验。
先由样本数据用Lp-范最小平差的方法计算p值,取不同值对应的密度函数参数估值的均值
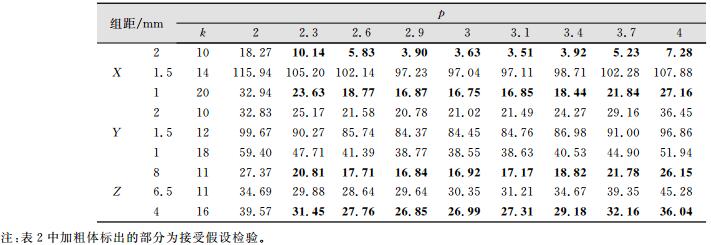
将RTK的观测误差分组划分区间时,X、Y方向上的组距分别为2 mm、1.5 mm、1 mm,Z方向上的组距分别为8 mm、6.5 mm、4 mm,且保证各组的npi>5,分组后相应的直方图见图 1。表 2为通过编程计算得到的在不同组距、不同p值下χ2统计量的值。
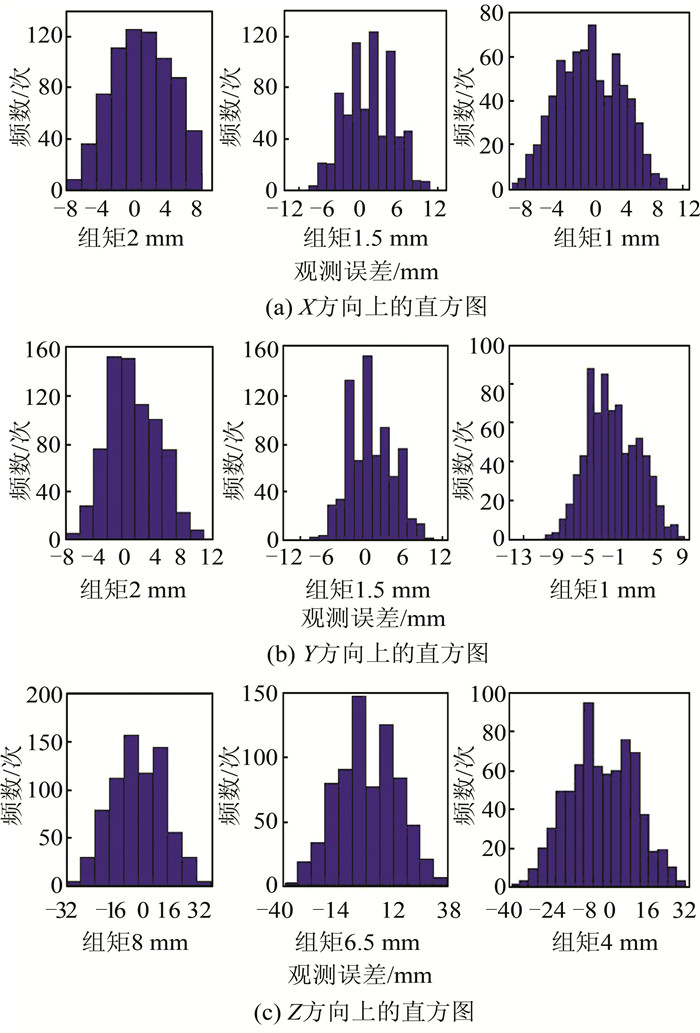 |
| 图 1 X、Y、Z方向上的直方图 Figure 1 Histograms of X、Y、Z |
| 表 2 不同p值下的χ2统计量 Table 2 χ2 Statistics Under Different p Values |
 |
接受域根据不同的显著水平α、划分区间k和参数个数m(在计算χ2前估计了
| 表 3 不同显著水平、自由度下(k=10、11、12、14、15、16、18、20)的皮尔逊χ2值 Table 3 Pearson χ2 Values at Different Significant Level and Freedom Degree(k=10、11、12、14、15、16、18、20) |
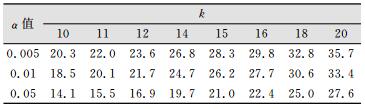 |
由表 2、表 3可以看出,在X、Y方向上组距为1.5 mm,Z方向上组距为6.5 mm时,所有p值下的分布都拒绝原假设,其直方图起伏也很没有规则,随机波动大。但对于RTK观测数据,当其精度在mm级,组距设为1.5 mm或6.5 mm时,RTK观测误差在统计时没有考虑其实际情况,会出现随机波动大的情况。因此在分组时,应该根据观测值的精度及观测值的有效位数综合考虑,以确定χ2值。
在X方向上,当组距为1 mm时,k=20,m=2,选取置信水平α=0.05,由表 2、表 3可以看出,正态分布(p=2)大于27.6,不能通过检验,但p在[2.3, 4]范围内均通过检验,接受原假设,由于χ2是度量实际观察次数与理论次数偏离程度的一个统计量,χ2越小,表明实际观察次数与理论次数越接近;χ2越大,表示两者相差越大。所以从最佳拟合的角度看,当p=3时,χ2值最小,因此对于这一组具体的观测数据,在进一步的研究中,取p=3的p-范分布作为其数学描述。
当组距为2 mm时,选取α=0.05,查表得χ1-α2(10-2-1)=14.1,由表 2可以看出,正态分布(p=2)大于14.1,不能通过检验,但p在[2.3, 4]范围内均通过检验;当p=3.1时,χ2值最小,这和组距为1 mm时有一致性(p值只相差0.1)。但通过编程计算发现,当组距为2 mm时,p在[4, 4.5]范围内也通过检验,但组距为1 mm却不能通过。若将理论值与实际值进行比较,则组距应小,这样检验结果较为可靠。
同理,在Z方向上,正态分布(p=2)不能通过检验,p在[2.3, 4]范围内均通过检验,其最佳拟合时p=2.9;但在Y方向上,p在[2, 4]范围内均不能通过检验。由图 1可以看出,Y方向上观测数据的观测误差分布不对称,其观测数据中可能有多峰情况,故不能通过检验。
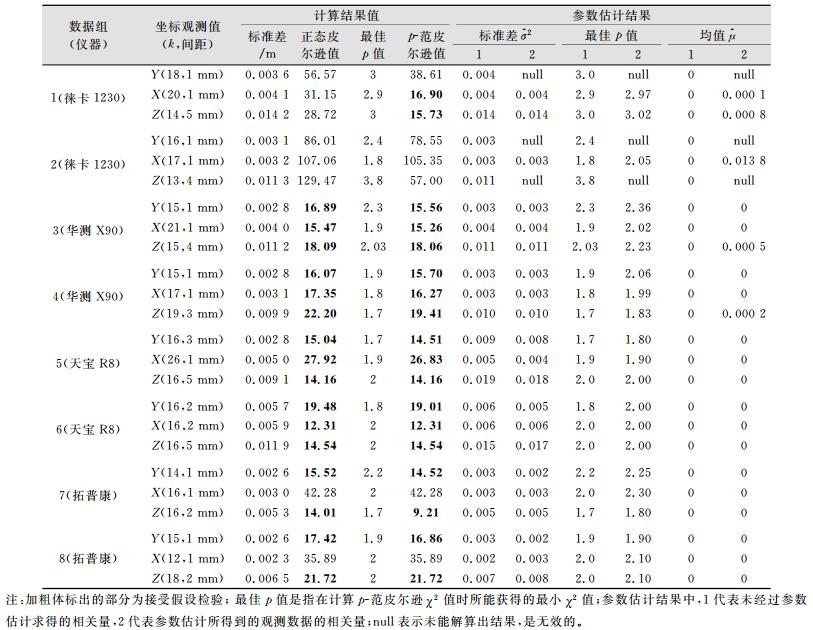
编程计算得到8组数据的χ2统计量的值,按照假设检验步骤依次进行正态分布检验及p取不同值时的假设检验,可以得到不同p值的χ2值,见表 4。
| 表 4 8组数据的计算结果值和参数估计值 Table 4 Calculation Results and Parameter Estimation Results of 8 Sets of Data |
 |
接受域根据不同的显著水平α、划分区间k和参数个数m(在计算χ2前估计了
| 表 5 不同显著水平、自由度下(k=12, 13, 14, 15, 16, 17, 18, 19,20,21, 26)的皮尔逊χ2值 Table 5 Pearson χ2 Values at Different Significant Level and Freedom Degree(k=12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 26) |
 |
① 华测X90和天宝R8所测值即使按最严要求(在显著水平α=0.05时),仍能通过正态分布检验,虽然最小χ2值也能通过p-范分布检验,但两者差异很小。
② 对于徕卡1230,数据1中X、Y、Z值均不服从正态分布,X值服从p-范分布(p-范值为2.9),Z值服从p-范分布(p-范值为3),Y值未通过检验;数据2的X、Y和Z均未通过检验,说明徕卡1230所测数据中可能存在除偶然误差之外的某种误差。正态分布和p-范分布均为单峰值函数,徕卡1230所测数据中有多峰情况,故不能通过检验。
③ 对于拓普康,数据7、数据8中Y、Z值均服从正态分布,X值既不服从正态分布,也不服从p-范分布。
④ 4种仪器的观测精度相当,8组数据的X和Y值精度均在3~4 mm(标准差),而Z值精度均在10~11 mm(标准差),然而4种仪器的概率密度函数却不完全相同。
2.5 参数估计编程对8组数据进行参数估计,验证其计算的正确性。通过MATLAB编程,得到的参数估计值结果见表 4。可以看出,华测X90、天宝R8、拓普康测得的数据经过参数估计所得到的结果(最佳p值、标准差、平均值)和未经参数估计所得到的结果基本一致。这说明通过综合运用这两种不同的统计推断方法,两者可以相互验证。参数估计的优点在于,当不清楚样本的分布情况时,可以用样本统计量去估计总体的参数,但是没有给出估计参数接近总体参数程度的信息。
3 结束语本文对24组GPS RTK数据分布进行了处理,实验数据是在流动站与基准站距离小于1 km的情况下采集的。实验后检查仪器,发现徕卡1230的数据链有故障,导致数据1和数据2出现多峰情况,应将徕卡1230所测的数据1、数据2排除。实例分析说明χ2检验是一个较好的方法。
长基线(大于10 km)的情况下,对流层误差、电离层误差只能采用模型改正的方法。这很难保证系统误差完全改正,那些没有完全改正的系统误差会当作偶然误差影响到观测值的概率密度函数,这将是下一步需要研究的工作。
| [1] |
刘大杰, 刘春. GIS空间数据不确定性与质量控制的研究现状[J]. 测绘工程, 2001, 10(3): 6-10. |
| [2] |
童小华, 史文中, 刘大杰. GIS中数字化数据误差的分布检验与处理[J]. 武汉测绘科技大学学报, 2000, 25(2): 79-84. |
| [3] |
李庆海, 陶本藻. 概率统计原理和在测量中的应用[M]. 北京: 测绘出版社, 1982.
|
| [4] |
孙海燕, 张方仁. p-范分布与p-范最小平差[J]. 武汉测绘科技大学学报, 1991, 16(4): 38-55. |
| [5] |
孙海燕, 潘雄. 一元p-范分布的参数估计[J]. 武汉大学学报·信息科学版, 2003, 28(10): 551-554. |
| [6] |
孙海燕. p-范分布的近似表示[J]. 武汉大学学报·信息科学版, 2001, 26(6): 222-225. |
| [7] |
蓝悦明, 贾媛. GPS观测值误差分布的研究[J]. 测绘通报, 2008(4): 12-13. |
| [8] |
蓝悦明, 王楠. GPS RTK观测数据的概率密度函数研究[J]. 测绘通报, 2011(2): 6-7. |
| [9] |
蓝悦明, 韩柯慧, 叶玲洁, 等. GPS RTK的概率密度函数初探[J]. 测绘地理信息, 2013, 38(5): 6-7. |
| [10] |
齐民友. 概率论与数理统计[M]. 北京: 高等教育出版社, 2002.
|
| [11] |
Verhagen S, Teunissen P J G. On the Probability Density Function of the GNSS Ambiguity Residuals[J]. GPS Solution, 2006, 10(1): 21-28. DOI:10.1007/s10291-005-0148-4 |
 2018, Vol. 43
2018, Vol. 43

