| 一种用于地铁区间地表沉降监测的改进方法 |
地表形变积累到某种程度会导致地表的沉陷或隆起,进而威胁地铁沿线建构筑物及人员的安全[1,2]。因此,有必要对地表区间进行周期沉降监测。郑州市地铁1号线西三环站至秦岭路站区间包括右线(长1 299.9 m)和左线(长1 296.609 m),左右线间距为13 m[3]。其中,左、右线各有900多米沿着建设西路成东西走向,布设的断面正好横穿建设西路。区间内建设西路分别与西三环路、工农路、华山路相交,交通环境复杂,车流量、人流量较大。
传统的地表沉降监测是按照《国家一、二等水准测量规范》实施的。根据《郑州市轨道交通1号线1期工程土建施工区间监测方案》中的监测周期及内容的要求,每次监测需把所测断面上的全部监测点通过水准线路连接起来。对城市地下穿行的地铁隧道而言,采用传统的监测方法就不可避免地要把仪器架设在机动车道上。这不仅会影响城市交通的正常运行,降低监测效率,最重要的是对监测人员及仪器设备的安全构成了重大威胁。为减少安全隐患,保证监测数据质量,本文对传统的监测方法进行了改进,通过工程实验,验证了新方法的可行性[4, 5]。
1 地表沉降监测改进方法郑州市地铁1号线西三环站至秦岭路站区间地表沉降监测通过布设断面来实现。该区间内沿线每隔20~30 m布设一条横断面,断面上横向测点的间距为3~7 m,横向测点的设置范围在隧道中心轴线两测各30 m的范围内[6]。区间断面图如图 1所示,每一断面监测点剖面图如图 2所示。
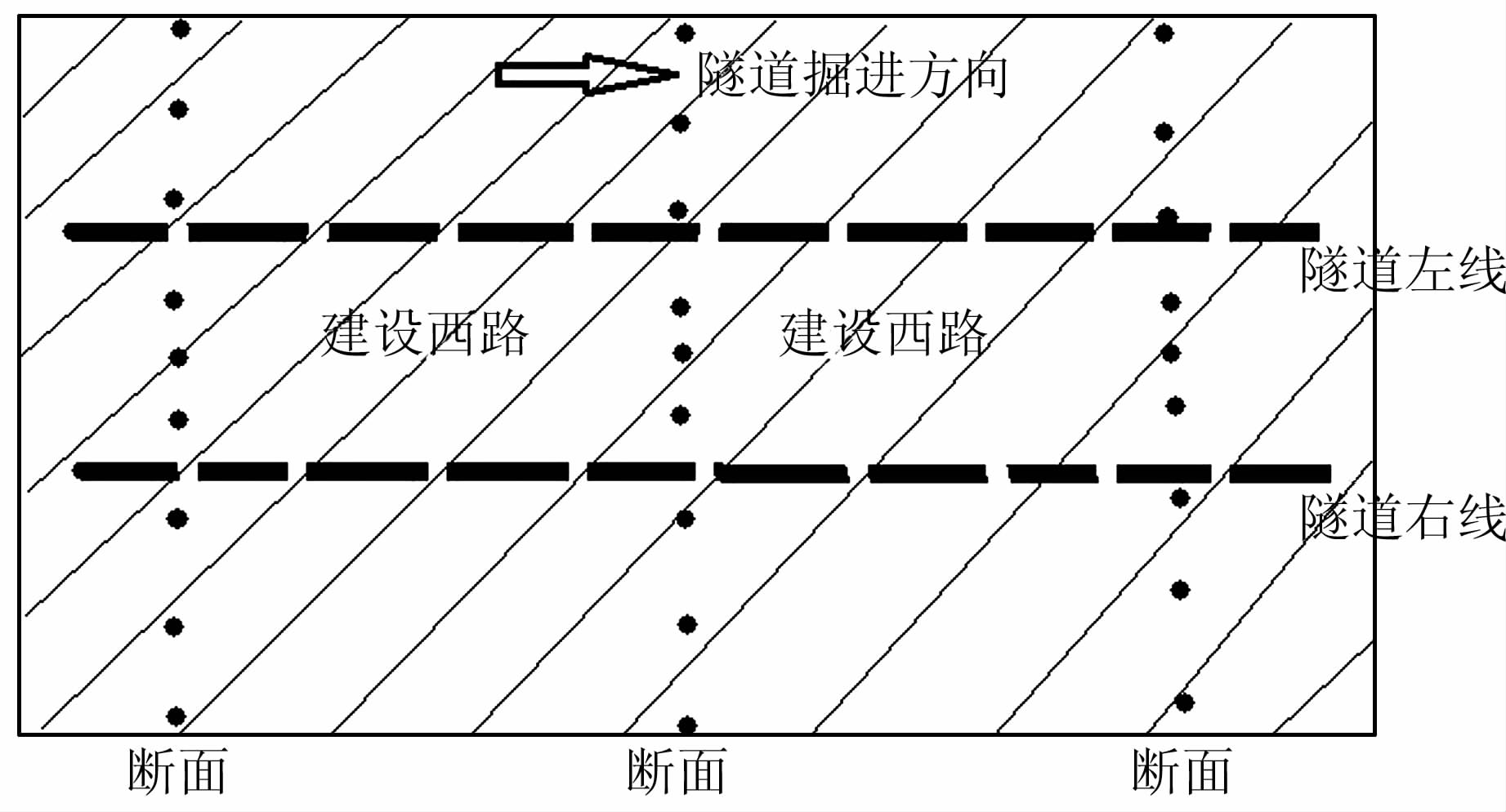 |
| 图 1 区间断面图 Figure 1 Sectional Drawing of Interval Section |
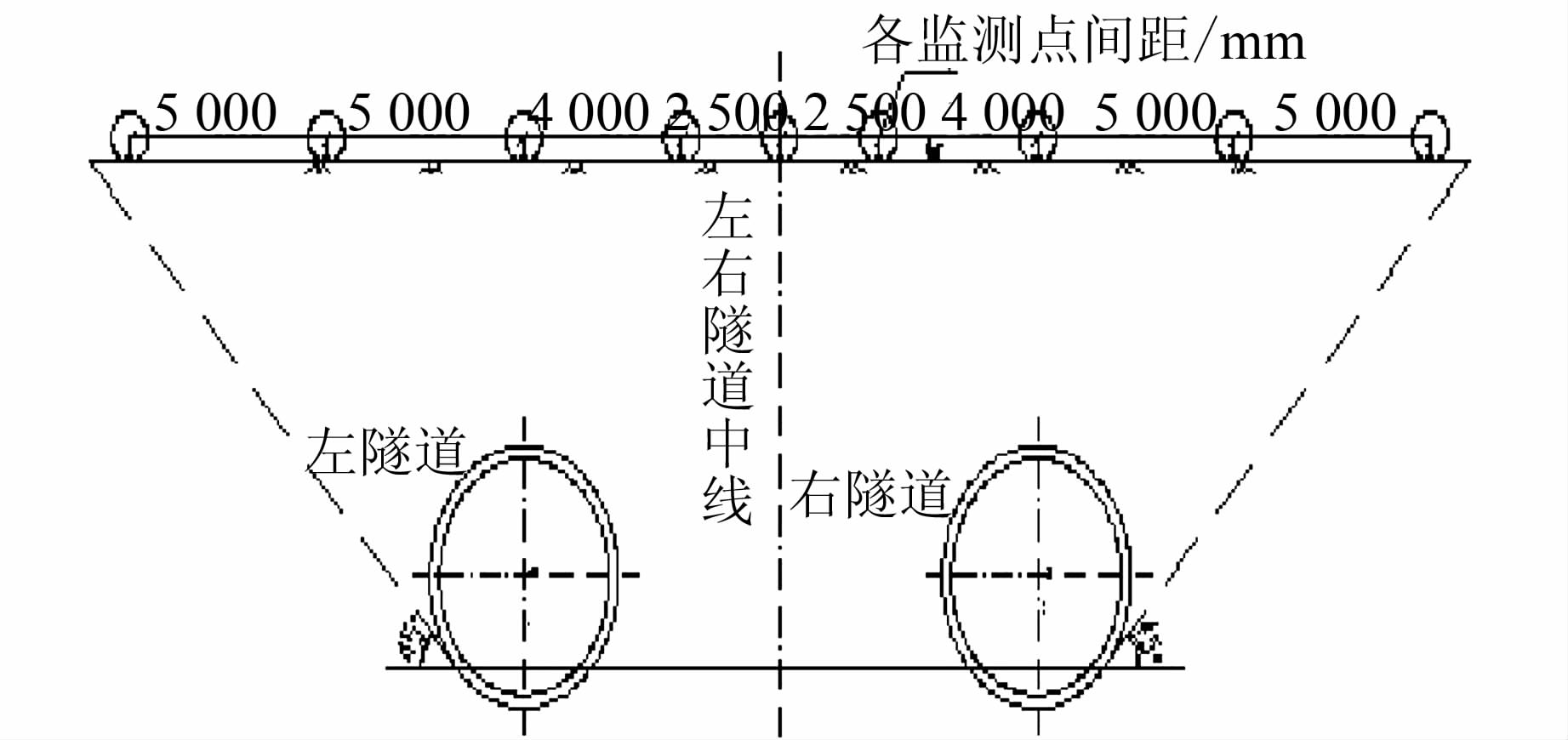 |
| 图 2 每一断面监测点的剖面图 Figure 2 Profile Map of Each Cross Section |
1.1 改进方法的实施步骤
为采集每个断面点的监测数据,传统监测方法按照线路测量模式把所测断面上所有的监测点连接起来构成一条附合或闭合的水准路线。施测时,从已知高程点出发,往测按奇数站后-前-前-后、偶数站前-后-后-前的观测顺序进行测量;返测时,对换前后水准尺,按奇数站前-后-后-前、偶数站后-前-前-后的观测顺序进行测量[7]。施测路线图如图 3所示。
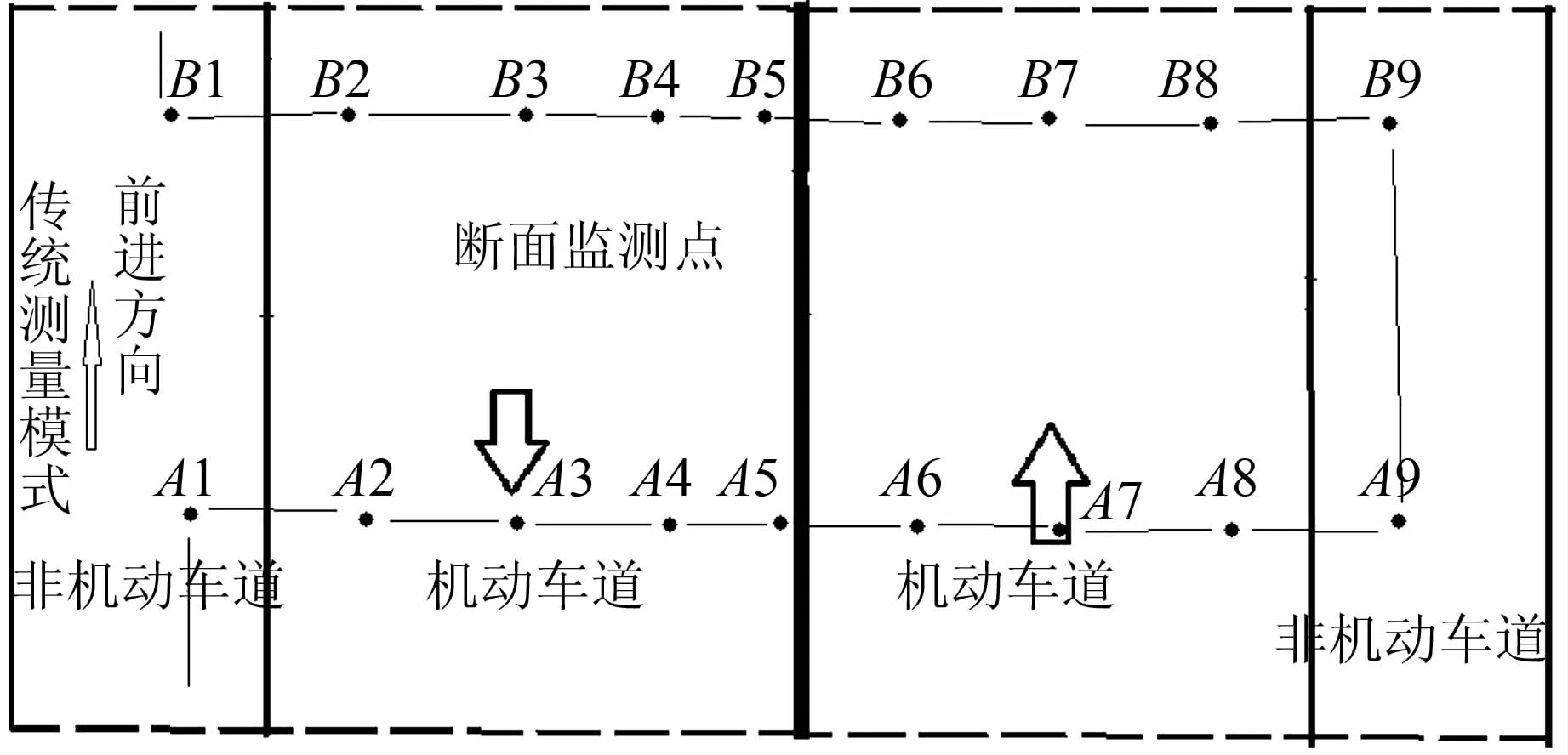 |
| 图 3 传统监测方法施测路线图 Figure 3 The Measuring Line Sketch of Traditional Monitoring Methods |
为了减小施测过程中人员和仪器设备的安全隐患,对线路测量模式进行改进,改进后采用线路测量模式结合中间点测量模式把所有监测点连接起来,构成附合或闭合水准路线。改进方法的观测流程图如图 4所示。
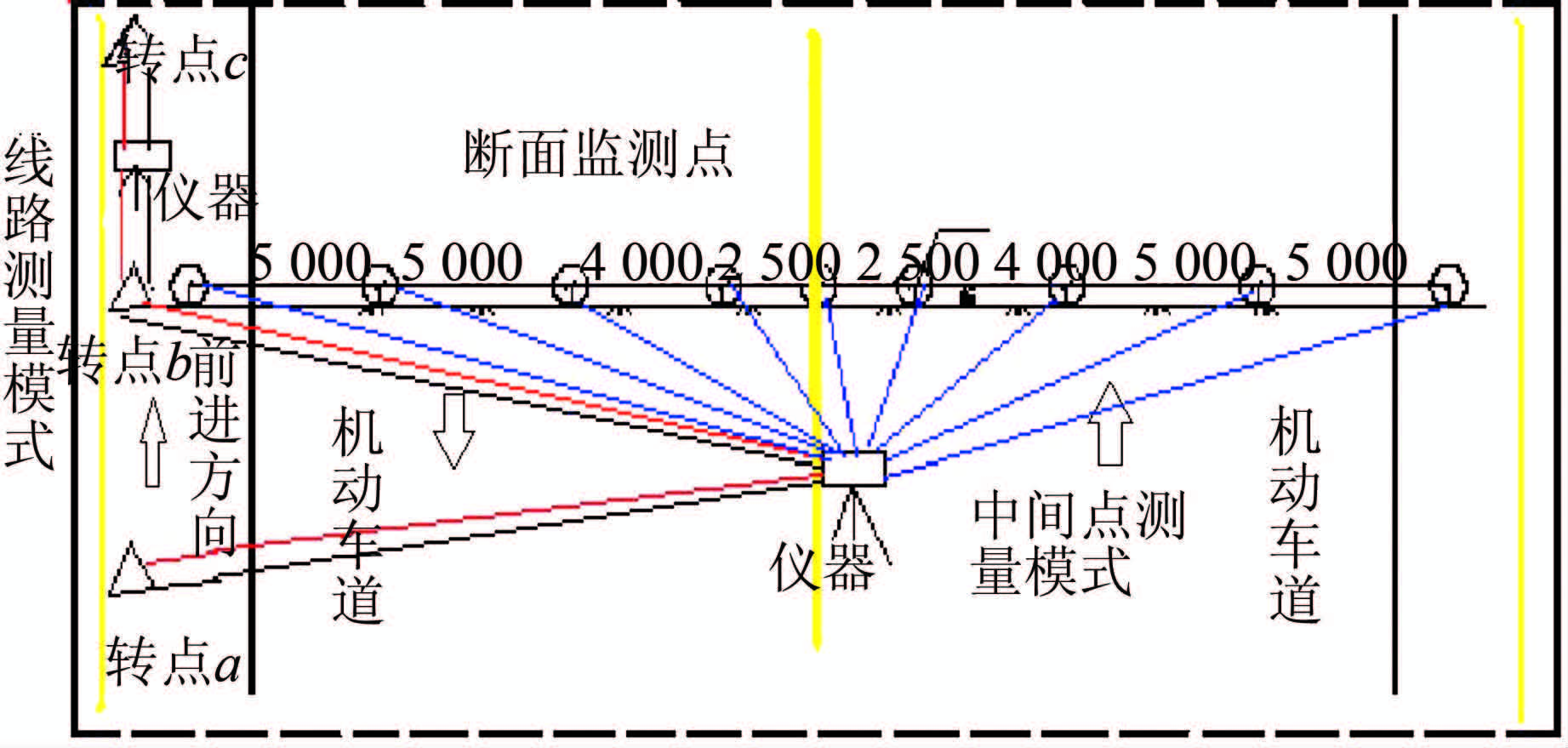 |
| 图 4 改进方法的观测流程图 Figure 4 The Flow Chart of Improved Method |
该方法的具体步骤如下:
1) 观测前准备工作。 施测前,监测人员接受安全教育及培训,了解道路交通安全法规,学习交通指挥手势。进场前,监测人员带上安全帽,穿上安全防护背心,确保安全。检定天宝DiNi12水准仪,确保各项指标合格。
2) 按线路测量模式进行测量。 往测时,新建一个文件,对水准仪进行设置后,选择线路测量模式,从一个已知的基准点开始,按奇数站后-前-前-后、偶数站前-后-后-前的观测顺序,沿着非机动车道或人行道前进,经过偶数个测站后到达转点a的位置(如图 4所示),完成该测站。
3) 仪器重新设置。 仪器迁到道路中央双黄线附近(如图 4所示),用安全桶在仪器前后30 m围一个警戒区。整平后,按奇数站后-前-前-后的观测顺序完成当前测站。完成测量后,在DiNi12水准仪中按下【功能键】,在仪器界面中,当前的线路测量模式切换到中间点测量模式。
4) 进行中间点测量。 切换到中间点测量模式施测时,后视基准为步骤3) 中最后一次后尺所测高程值,即图 4中转点a的读数。在中间点测量模式下依次观测断面上的监测点,完成测量并记录在仪器中。
5) 回到线路测量模式继续测量。 通过功能键切换,再次回到线路测量模式,沿机动车道或人行道继续线路测量(如图 4中前进方向),遇到需要测量测断面时,重复步骤3) ~5) ,直到完成该水准路线。返测时,互换前后水准尺,按奇数站前—后—后—前、偶数站后—前—前—后的观测要求,重复步骤2) ~5) 即可。
1.2 改进方法的高程计算1) 线路测量模式高程的计算
传统的测量方法(线路测量模式)构成一条单一的水准路线,数据解算依据《国家一、二等水准测量规范》中的限差要求进行,若限差不满足要求,需分析情况,重新测量线路;若限差满足要求,通过数据线将测量数据导入计算机内,进行后处理。单一水准路线各测段的高差改正数按下式计算:
| ${{v}_{i}}=\frac{{{f}_{h}}}{\left[ L \right]}\cdot {{L}_{i}}$ | (1) |
式中,L为距离;fh为闭合差。
根据已知的高程点和改正后的高差计算中途站点的高程,即
| $H={{H}_{0}}+\sum h\prime +\sum v$ | (2) |
式中,H0为已知高程;h′为高差;v为高差改正值。
2) 中间点测量模式高程的计算 在计算中间点测量模式中监测点的高程时(如图 4所示),转点a的高程值作为中间点测量模式中的后视基准点。转点a的高程可以在线路测量模式下由式(2) 求出。
设线路测量时后尺的读数为k1、k2,切换到中间点测量模式后,前尺的读数为m1、m2、…、mn,其中,n为某一断面上监测点的个数。则断面上监测点的高程计算公式如下:
| ${{H}_{i}}={{H}_{a}}+\left[ \frac{{{k}_{1}}+{{k}_{2}}}{2}-{{m}_{i}} \right],i=1,2,\ldots ,nn=9$ | (3) |
根据式(3) 可以计算出往测和返测时断面上每个监测点的高程值,比较往返测所测的Hi,若两次计算的高程值较差小于0.6 mm,认为数据可靠。
1.3 改进方法的误差影响及精度评价改进后的监测方法是否可用,主要看其精度是否达到设计要求。郑州市地铁1号线西三环站至秦岭路站区间地表沉降监测中,传统方法是采用线路测量模式进行水准线路测量,改进后的方法是在水准线路的测量过程中,采用线路测量模式与中间点测量模式相结合的方法来测量,和传统方法相比,改进方法的主要误差源是因前后视距不相等引起,主要表现为i角误差。
由郑州市地铁1号线地表监测断面的设计(见图 2) 可知,监测点距两隧道中心点最远的距离为16.5 m,假设仪器就架设在两隧道的中点位置,后视基准点为距离隧道中心最远的监测点。采用中间点测量模式时,两次读数的前后视距差都会小于14 m (距隧道中轴线最近的监测点为2.5 m)。假设i角为15″(一、二等水准测量要求i角的绝对值小于15″),前后视距差为14 m,则由i角引起的测量误差
改进方法和传统方法相比,原理上一致。不同的是在数据处理时,改进方法需要求出中间点测量模式中后视点的高程值,并不破坏传统的线路测量模式,故改进方法的精度评价方法和传统方法一致。即偶然中误差MΔ按测段往返测高差不符值计算,具体公式为:
| ${{M}_{\Delta }}=\pm \sqrt{\frac{1}{4n}[\frac{\Delta \Delta }{L}]}$ | (4) |
式中,Δ为各测段往返测的高差不符值,单位为mm;L为各测段的距离,单位为km;n为测段数。
2 工程实验及结果分析为了验证改进方法是否可行,在郑州市地铁1号线西三环站至秦岭路站区间地表沉降监测中,采用传统方法和改进方法分别对区间地表上第4、5、6断面进行测量,其中第4断面的1、2号点被障碍物覆盖,没有测量值。对测量数据进行处理,所得结果见表 1、表 2。
| 表 1 传统方法测得的断面监测点高程值/m Table 1 The Section Monitoring Height Value of Traditional Method/m |
 |
| 表 2 改进方法测得的断面监测点高程值/m Table 2 The Section Monitoring Height Value of Improved Method/m |
 |
表 1中4、5、6断面监测点的高程值采用传统方法测量计算得到,表 2中4、5、6断面监测点的高程值采用改进方法测量计算得到。用传统方法计算得到的各断面上监测点的高程值减去改进方法中对应断面对应监测点的高程值,得到的计算值见表 3。
| 表 3 两种方法得到的高程值的较差/mm Table 3 The Differences of Elevation Values by Two Methods/mm |
 |
从表 3可看出,从整体上看,4、5、6断面有效监测点共25个,各监测点较差中大于零的有3个点,小于等于零的有22个,较差平均值为-0.3 mm。与比传统方法计算的高程值相比,改进方法计算的高程值整体偏大,具有系统性。在地铁区间地表沉降监测中,需要知道的是监测点的高程变化速率,也就是说改进方法的整体性变化可在求高程变化速率中得到消除。因此,改进后的方法适用于郑州市地铁1号线地铁区间地表沉降监测[6,8]。
两种方法所测得的高程差的最大值为4断面的8号点,差值为-0.7 mm;最小值为6断面的2、3、7号点,差值为0 mm。从局部看,两种方法计算得到的高程较差中,4断面平均较差-0.53 mm,5断面平均较差-0.33 mm,6断面平均较差-0.09 mm。结合盾构机掘进程度来看,盾构正好掘进到4断面和5断面之间,4断面和5断面有沉降,6断面相对稳定,符合形变规律。
3 结束语1) 与传统监测方法相比,改进方法能够大大减少监测人员和仪器面临的安全隐患,提高了监测的效率。
2) 采用改进方法测量时,在前后视距差小于30 m、电子水准仪i角小于15″的情况下,i角对断面上监测点引起的误差小于2 mm,满足地铁区间监测方案的规定。
3) 改进方法与传统方法的精度评定方法一致,数据解算时,改进方法需根据传统方法解算出的数据进行解算,求出改进方法的高程测量值。
4) 工程实验表明,与比传统方法计算的高程值相比,改进方法计算的高程值整体偏大,具有系统性,适用于郑州市地铁1号线地铁区间地表沉降监测。结合盾构机掘进程度来看,盾构正好掘进到4断面和5断面之间,4断面和5断面有沉降,6断面相对稳定,符合形变规律。
| [1] |
周顺华.
城市轨道交通结构设计与施工[M]. 北京: 人民交通出版社, 2011 : 136 .
Zhou Shunhua. Structural design and construction of urban rail transit[M]. BeiJing: People's traffic press, 2011 : 136 . |
| [2] |
张恒, 陈寿根, 邓稀肥. 盾构掘进参数对地表沉降的影响分析[J].
现代隧道技术,2010,(05) : 48–51.
Zhang heng, Chen Shougen, Den Xifei. Analysis of the influence of shield Driving Parameters on Ground Settlements[J]. Modern tunnelling technology,2010,(05) : 48–51. |
| [3] |
中铁十一集团项目部.郑州市轨道交通1号线1期工程土建施工区间监测方案[G].中铁十一局集团,2010 The project department of China railway 11 group. The Interval monitoring programme of civil engineering construction for No.1project of Zhengzhou rail transit line 1[G]. China railway 11 group,2010 |
| [4] |
GB 12897-2006,国家一、二等水准测量规范[S].北京,中国标准出版社,2006 GB 12897-2006, State one, second-class leveling specification[S].BeiJing, China standard publishing house,2006 |
| [5] |
GB 50308—2008,城市轻轨交通工程测量规范[S].北京,中国建筑工业出版社,2008 GB 50308—2008, Urban light rail traffic engineering surveying specifications[S].BeiJing, China building industry press,2008 |
| [6] |
夏志强, 周传波, 平雯, 刘杨波. 地铁隧道盾构法施工地表沉降特征及预测研究[J].
城市轨道交通研究,2014,(10) : 98–99.
Xia Zhiqiang, Zhou Chuanbo, Ping W en, Liu Yangbo. Characteristies and Prediction of the surrace Subsidence on Metro Shielding Tunnel[J]. Urban rail transit,2014,(10) : 98–99. |
| [7] |
张福利. DiNi 12电子水准仪在沉降监测中的运用[J].
山西建筑,2008,34(33) : 350–351.
Zhang Fu-li. Application of DiNi 12 electronic level in sedimentation observation[J]. Shanxi building,2008,34(33) : 350–351. |
| [8] |
陈浩, 张建坤. 盾构长距离下穿式平瓦房沉降监测分析[J].
测绘地理信息,2013,38(5) : 32–33.
CHEN Hao, ZHANG Jiankun. Settlement Observation and Analysis of Shield Tunneling Crossing Old Flat Tile-Roofed House[J]. Journal of Geomatics,2013,38(5) : 32–33. |
 2016, Vol. 41
2016, Vol. 41

