| 利用有限元法的大坝变形分析研究 |
2. 61206部队,辽宁 大连,116023
2. 61206 Troops, Dalian 116023, China
我国是地震多发的国家,建设重力坝的地区一旦发生地震,将带来灾难性的后果。在修建大坝设计中将地震荷载纳入考虑范围,考察重力坝在地震荷载下的动力响应特性,研究重力坝在静力、动力荷载下的安全问题具有十分重要的意义[1, 2]。
国内外诸多学者用各种非线性模型分析了混凝土重力坝在地震作用下的反应[3]。然而,总体来看,大坝安全评价准则目前正处在发展阶段,如何有效合理地利用有限元计算结果受到广大研究者的普遍关注。国内学者也提出了一些评价方法,如沈怀至等[4]釆用数值方法构造了大坝-地基系统的地震易损性,提出了坝体-地基系统的地震易损性评价方法;杜荣强、林阜等[5]用弹塑性损伤模型对大坝进行了地震损伤分析,并指出损伤力学中的损伤指标可以为混凝土结构提供比较合适的安全评价标准。目前来看,这些指标还没有得到广泛的认同,需要更进一步的研究。
目前,常使用的重力坝稳定分析方法[6]有3种:刚体极限平衡法、有限元法、地质力学模型试验法。有限单元法是目前使用较多的一种方法。该方法可以计算地基在受力后的应力及位移,可以直观地反映坝与地基破坏的状态,但该方法得出的稳定失效的判断依据仅作为参考。本文使用有限元法[7]计算重力坝的应力,使用反应谱法计算重力坝的地震响应。反应谱法已被世界许多国家广泛接受,我国的抗震规范[8]中也使用了反应谱方法,这与水工的建筑物较为符合。影响混凝土坝安全稳定的因素有很多,如坝基扬压力、上游水位高程、地震、温度和自身结构材料等。由于篇幅所限,本文主要就由水位高程及地震作用引起的坝顶水平位移进行变形分析,并与坝顶激光准直测量的实测数据进行对比分析。
1 工程背景及模型的简化某混凝土大坝是一座以防洪、灌溉、供水等为主的综合型大型水利枢纽工程,为混凝土重力坝,一级建筑物。坝体分成4个碾压坝段:左挡水碾压坝段、溢流碾压坝段、底孔碾压坝段、右挡水碾压坝段。
根据《混凝土重力坝设计规范》(SL319-2005) 的规定[8]及该坝本身建筑结构,荷载与计算参数的取值如下:混凝土重力密度rc=2.4×104N/m3,弹性模量Ec=18.5×109N/m2,泊松比μc=0.167;地基岩石重力密度rr=2.75×104N/m3,弹性模量Er=18×109N/m2,泊松比μr=0.275。设计洪水位为131.5 m,相应下游水位为101.38 m;正常高水位为127.0 m,相应下游水位为94.0 m;坝底高程为85.0 m。
由于重力坝沿坝轴线方向用横缝分割成若干个独立的坝段,所以对该坝的变形分析可以按平面问题来处理,单独选取27#拦水坝段进行二维建模分析[9, 10]。27#段面图如图 1所示,将其建模简化为如图 2所示的模型图,进而进行有限元数值模拟变形分析。
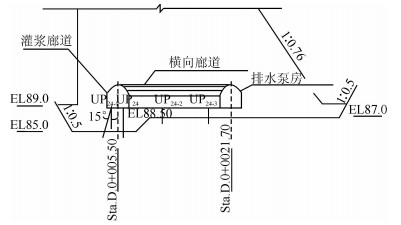 |
| 图 1 27#坝体段面图 Figure 1 Section Figure of 27# Dam |
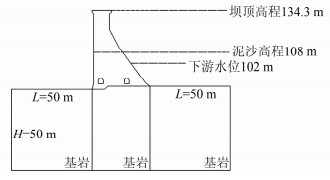 |
| 图 2 简化模型图 Figure 2 Diagram of Simplified Model |
2 有限元法静力分析坝顶水平位移
有限元静力法分析坝顶水平位移流程如图 3所示。考虑设计规范中动力分析的地震影响,对该坝的静力分析采用正常蓄水位。计算时,对ANSYS14.0有限元软件进行相关设置,网格划分及施加约束条件如图 4所示,静力求解后得到坝体变形图如图 5所示,在正常蓄水位情况下的坝顶水平位移如图 6所示,垂直位移如图 7所示。
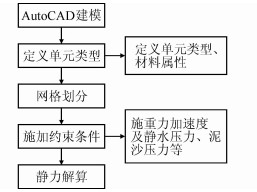 |
| 图 3 有限元静力法分析坝顶水平位移流程图 Figure 3 Flow Chart of Dam Top Horizontal Displacement Using Finite Element Static Analysis |
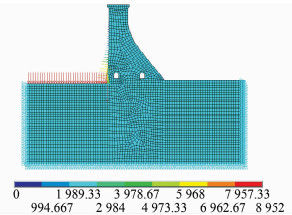 |
| 图 4 网格划分图 Figure 4 Diagram of Grid Division |
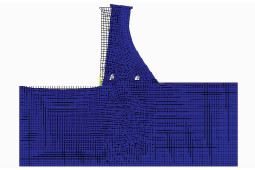 |
| 图 5 坝体变形图 Figure 5 Diagram of Dam Deformation |
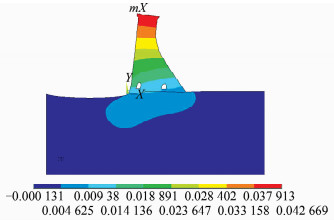 |
| 图 6 坝体变形水平位移图 Figure 6 Horizontal Displacement of Dam Deformation |
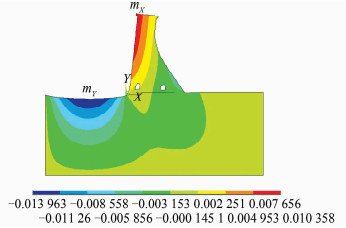 |
| 图 7 坝体变形垂直位移图 Figure 7 Vertical Displacement of Dam Deformation |
由于激光准直测量仪器是实时对坝顶水平位移进行监测并记录的,其数据量非常庞大,因此,对所有数据进行筛选分析,2014年部分激光准直测量数据如表 1所示。
| 表 1 2014年激光准直测量数据(部分) Table 1 Laser Alignment Measuring Data in 2014 (Part) |
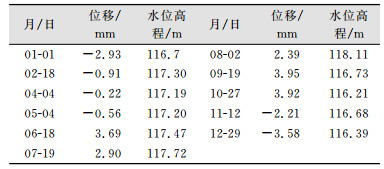 |
通过静力求解,对图 5、图 6、图 7分析得出,在蓄水位工况下,该坝的坝顶水平位移为0.043 908 m,垂直位移为0.013 963 m。通过图 5可以看出坝体内部每一节点处的位移变化情况,进而分析每一点的变形破坏程度。通过图 6和图 7可以看出坝顶的位移变化最大,且受到的破坏形变也最大。
对实测水位高程118 m采用上述理论分析,得出坝顶水平位移为0.011 m,而对坝顶激光准直测量的实际监测数据进行统计分析[11],得出2014年实测坝顶水平位移变化区间为(-3.58,3.95) mm。而通过多年的数据统计分析得到坝顶位移最大变化为1 cm左右,与有限元数值模拟结果1.1 cm接近,可见模型选择合理,有限元变形分析结果具有一定的可靠性。
3 有限元法动力分析坝顶水平位移有限元法动力分析是在静力分析的基础上,采用反应谱分析的方法进行,数值模拟出设计地震烈度对大坝坝顶水平位移的影响,同时也可模拟出各阶振动频率下的变形位移[12]。有限元动力分析流程为:静力求解→模态分析→反应谱分析→模态扩展分析→合并模态求解。本文对该坝进行了18阶的振动变形分析。其中前4阶坝体对大坝的位移影响分别为1.694 mm、0.864 mm、1.364 mm和0.985 mm。
通过模态分析坝顶节点位移响应谱曲线如图 8所示,可以看出,地震对该混凝土大坝水平位移的最大影响发生在第一阶,为1.694 mm。在设计地震烈度情况下,地震对大坝坝顶水平位移影响为毫米级,影响不大,坝体结构相对稳定。
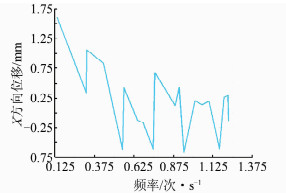 |
| 图 8 X向位移响应谱曲线 Figure 8 X Displacement Response Spectrum Curve |
4 结束语
本文就某大型水库大坝的变形分析采用了有限元数值模拟的方法,得出该坝的坝顶水平位移,并将其与实测数据进行对比分析,认为该坝目前及未来一段时间处于安全稳定状态。同时,对该坝进行了地震动力学分析,模拟了在设计地震烈度情况下坝体各阶模态的变形情况。分析认为,在设计地震烈度情况下,地震对该混凝土坝的影响很小,该坝具有一定的抗震性能。对该混凝土坝的静力、动力分析的结果充分表明,该坝在运营过程中一直保持着安全稳定状态。
| [1] | 兰永新, 马晓光, 阮晓宁. 新疆某水库大坝变形监测方法研究[J]. 新疆地质, 2007, 25(4): 440–443 |
| [2] | 黄德伦, 廉琦, 孙利军, 等. 基于大坝变形监测预报的神经网络方法的对比分析[J]. 北京测绘, 2014, (2): 10–16 |
| [3] | 徐俊样, 刘西拉. 混凝土初始损伤模拟和在混凝土重力坝抗震分析中的应用[J]. 上海交通大学学报, 2006, 40(6): 1038–1041 |
| [4] | 沈怀至, 金峰, 张楚汉. 基于性能的重力坝-地基系统地震易损性分析[J]. 工程力学, 2008, 25(12): 86–91 |
| [5] | 杜荣强, 林皋, 胡志强. 混凝土重力坝动力弹塑性损伤安全评价[J]. 水利学报, 2006, 37(9): 1056–1062 |
| [6] | 姜兴阁. 论变形监测技术的现状与发展趋势[J]. 矿山测量, 2012, (4): 7–10 |
| [7] | 黄国权. 有限元法基础及ANSYS应用[M]. 北京: 机械工业出版社, 2004 |
| [8] |
SL319-2005, 混凝土重力坝设计规范[S]. 北京: 水利水电出版社, 2005 |
| [9] | 许贝贝, 崔晨风. 大坝自动化监测数据粗差处理方法研究[J]. 测绘地理信息, 2015, 40(2): 59–61 |
| [10] | 葛修润, 任建喜, 李春光, 等. 三峡左厂3#坝段深层抗滑稳定三维有限元分析[J]. 岩土工程学报, 2003, 25(4): 389–394 |
| [11] | 黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2003 |
| [12] |
熊健. 混凝土重力坝的抗震安全评价分析[D]. 大连: 大连理工大学, 2012 |
 2017, Vol. 42
2017, Vol. 42

