| 自动化变形监测的精密测距三角高程测量研究 |
变形监测工程中的垂直位移监测有精密水准和静力水准两种方法。为了提高监测效率和提供实时监测数据,需实现变形监测自动化,如采用测量机器人进行自动化监测,同时提供三维空间信息,即进行水平位移监测的同时进行精密测距三角高程测量。许多学者对三角高程测量代替几何水准测量进行了研究和精度分析[1-4]。鉴于工程建筑物是监测目标点在垂直方向上的变动,只需要测定目标点的变形量及累计变形量[5],不一定需要变形点的准确坐标,而且在进行周期监测中,各周期含有一些系统误差,如仪器固定误差、棱镜常数误差、地球曲率引起的球差以及大气折光引起的气差等,在计算变形量及累计变形量时,可以得到一定的抵消和消除。因此,本文提出了用自动化三角高程测量代替精密水准测量的自动化垂直位移监测方法,并进行了理论分析和实验验证。
1 测距三角高程精密测量及其自动化 1.1 测距三角高程测量的误差分析三角高程测量有视距法和精密测距法两种方法,采用测量机器人属于后一种,是根据全站仪从测站向照准点观测竖角和斜距,计算两点间的高差[6]。除需要采用高精度智能型全站仪外,为了减弱垂直大气折光的影响,可进行多时段多测回观测,注意视线离地面有一定高度,选择垂直大气折光变化对称的时间 (如在上、下午) 进行两时段多测回观测。AB两点间的高差hAB为:
| $ \begin{align} &{{h}_{AB}}=D\cdot \left( \tan {{\alpha }_{1}}+\tan {{\alpha }_{2}} \right)/2+ \\ &\frac{2-\left( {{k}_{2}}+{{k}_{1}} \right)}{4R}{{D}^{2}}+\left( {{i}_{1}}+{{i}_{2}}-{{v}_{1}}-{{v}_{2}} \right)/2 \\ \end{align} $ | (1) |
式中, R为地球半径;D为平距;α为垂直角;k为大气折光;i为仪器高;v为棱镜高。
由于α1≈α2, 用α表示,2-(k2+k1)=Δk, ma1=ma2=ma, mi1=mi2=mv1=mv2=miv, 可得高差中误差为:
| $ \begin{align} &m_{{{h}_{ab}}}^{2}=\left( {{\tan }^{2}}a+\frac{\Delta {{k}^{2}}{{D}^{2}}}{4{{R}^{2}}} \right)m_{D}^{2}+ \\ &\frac{{{D}^{2}}}{2{{\cos }^{4}}\alpha }\cdot \frac{m_{\alpha }^{2}}{{{\rho }^{2}}}+{{\left( \frac{{{D}^{2}}}{4R} \right)}^{2}}m_{\Delta k}^{2}+m_{iv}^{2} \\ \end{align} $ | (2) |
| $ m_{D}^{2}={{\cos }^{2}}\alpha \cdot m_{s}^{2}+\frac{{{\sin }^{2}}\alpha }{{{\rho }^{2}}}m_{\alpha }^{2} $ | (3) |
式 (3) 中等式右边第2项为微小量,可忽略不计,采用TCA2003, mD≈ms=±1.5 mm。表 1为影响三角高程测量精度的主要因素。
| 表 1 三角高程测量误差分析表 Table 1 Error Source Analysis Table of Trigonometric Leveling |
 |
因此,当mΔk控制得好时,α误差的影响最大,是三角高程测量的主要误差来源[7];Δk的误差对高差影响次之,而D的误差对高差的影响很小。当D>600 m时,Δk的影响会急剧增大,所以D不宜过大。并且mΔk的控制也非常重要,当较大时,该项引起的误差甚至比垂直角误差的影响还要显著。
1.2 自动化测距三角高程监测及实现自动化变形监测通常将测量机器人固定架设在工作基点上,在基准点及变形点上埋设强制对中棱镜,利用测量机器人变形监测自动化系统,测量机器人自动对基准点、监测点采用全圆方向法进行边角测量[8],并采用距离差分、角度差分等技术进行数据处理,得到基准点、工作基点以及监测点的三维坐标,从而得到监测点的三维变形数据,其垂直位移是通过三角高程测量方法得到的,垂直位移变形量为本次测量高程与上次测量高程之差,垂直位移累计变形量为本次测量高程与第一次测量高程之差。
利用自动化监测软件可以自动进行距离和垂直角改正,输出点位差分改正后的数据。点击数据整理→数据后处理→差分处理方式,则会弹出如图 1所示的对话框。
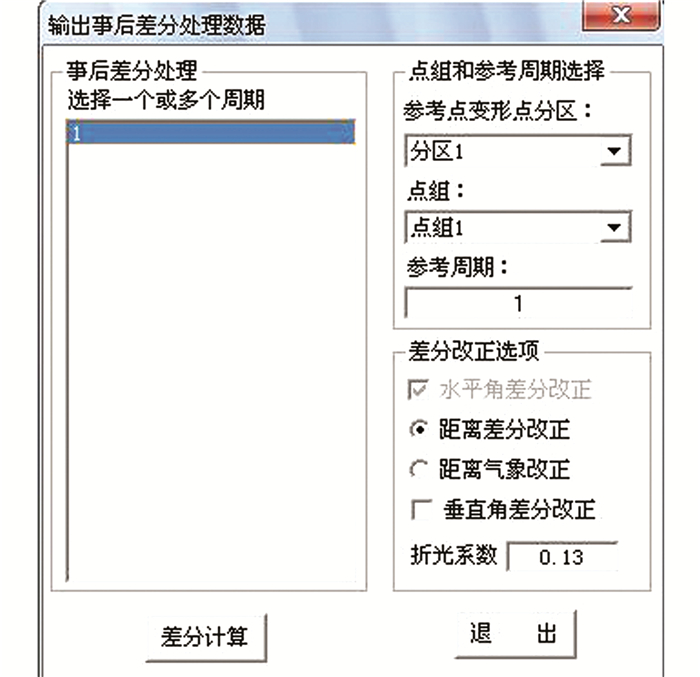 |
| 图 1 数据差分处理 Figure 1 Differential Data Processing |
距离气象改正是根据气象改正公式计算距离改正数,每期观测时精确记录测站位置的温度、气压,进行气象参数改正。
距离差分改正是根据所测距离与已知距离的差建立改正模型来改正距离的,可以利用变形监测基准点和工作基准点 (测站点) 相对稳定的特征,在无需测量气象元素的基础上,实时差分改正大气折射率、温度、气压对距离的影响。当视线条件相似的条件下,距离差分可显著提高距离精度。设测站点至基准点的已知斜距为S0,在变形监测过程中,某一时刻实测的斜距为S1,两者之间的差异可以认为是由气象条件变化引起的,按下式可求出气象改正比例系数KS:
| $ {{K}_{S}}=\frac{{{S}_{0}}-{{S}_{1}}}{{{S}_{0}}} $ | (4) |
通过采用多个基准点测定的气象改正比例系数的平均值来保证其可靠性。然后通过气象改正系数与基准点、监测点的距离 (S测) 乘积可以得到相应的距离气象改正数 (S改):
| $ {{S}_{改}}={{K}_{S}}\cdot {{S}_{测}} $ | (5) |
高差差分改正是指用已知值计算的垂直角与观测的垂直角之差建立改正模型对垂直角进行改正。大气折光是单向三角高程测量的主要误差来源,利用变形系统的稳定基准点存在的多个固定高差,求得每期的大气折光系数,对变形点的高差进行差分改正,从而提高三角高程的监测精度。
2 实例分析 2.1 项目及监测概况某基坑长530 m,宽280 m,开挖深度为13.6 m,共布设81个支护结构顶部水平位移及垂直位移监测点,水平位移与垂直位移监测点为同一点位,设计要求水平位移及垂直位移监测精度达到1 mm。垂直位移通常采用几何水准施测。为提高作业效率及提供实时的变形监测数据,布设混合基准网,利用测量机器人按极坐标法进行自动化变形监测,监测点采用强制对中埋设,工作基点采用强制对中观测墩。采用测量机器人变形监测自动化系统 (GeoRDMAS) 控制测量机器人进行自动变形监测,以及对监测过程中所采集的数据进行管理与处理[9],该系统具有自动测量、实时显示测量成果、实时显示变形趋势、自动进行气象改正等功能。
变形监测网如图 2所示,由6个基准点 (J1 ~J6) 和6个工作基站点 (GJ1 ~GJ6) 组成,混合基准网平均边长240 m左右,方向观测值数为34,边长观测值数为23,平均多余观测数为0.684,工作基点的高程精度小于0.5 mm,边长精度达0.5 mm。采用两台测量机器人进行周期观测,从2012-09-15到2014-05-20,共进行了191期监测,保证了支护结构的稳定和施工安全。
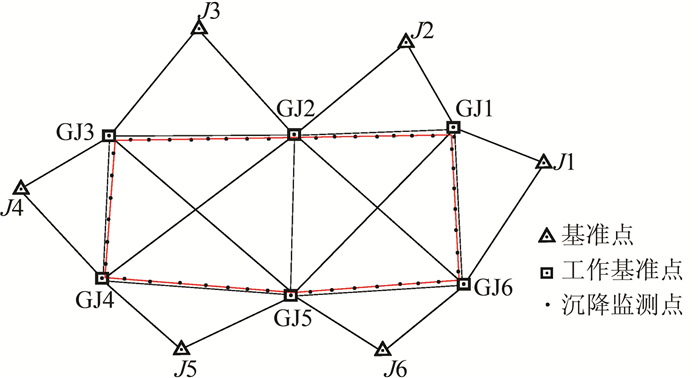 |
| 图 2 某基坑混合基准点图 Figure 2 Reference Points Map of a Foundation Pit |
2.2 精度分析
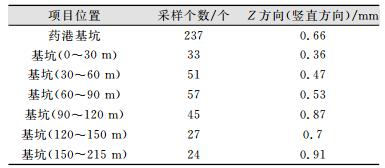
为了减弱垂直大气折光的影响,进行多时段多测回观测,选择离地面较高的视线,且每条三角高程路线进行异午两个时段观测,每个时段的时间选择上、下午垂直大气折光变化对称的时间。对未受施工影响或施工前测得的基坑变形监测的多点、多周期监测成果,即通过对监测点未发生变形时的监测成果进行精度统计,作为本项目自动化变形监测的实际三角高程监测精度。其中变形监测仪器到监测点的最长边为215 m,最短边为20 m,统计出通过自动化监测三角高程精度为±0.66 mm,见表 2。
| 表 2 基坑工程预警系统应用监测精度统计表 Table 2 Monitoring Accuracy Statistics of Foundation Pit Early-warning System |
 |
同时为检验自动化监测三角高程的准确性和可靠性,选取20条边的三角高差进行改正计算,并取上、下午两个时段均值做高差观测值,并将对应于一等水准测量的基准点作为平差起算数据,用COSA软件进行平差计算[10],将其结果与使用DINI03水准仪一等水准成果进行比较,结果见表 3。
| 表 3 自动化三角高程平差成果及其与一等水准成果比较表 Table 3 Comparison of Automatic Trigonometric Leveling Adjustment Results and Its First-class Results |
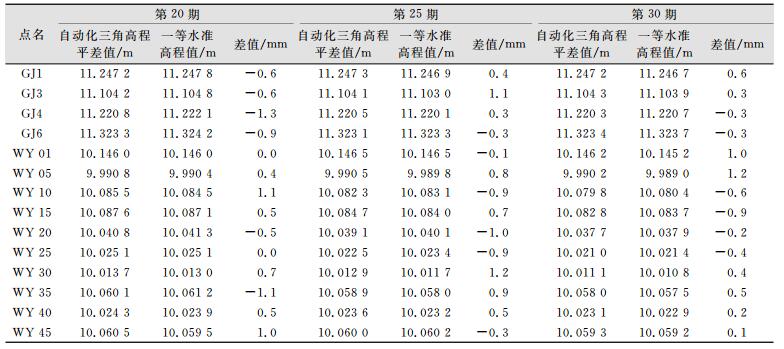 |
由表 3可见,所有14个点共42个自动化三角高程与一等水准高程较差都在1.3 mm以内,且有34个小于1.0 mm,可以求得自动化三角高程测量的成果精度为0.69 mm,小于1.0 mm,由此说明非同时对向观测自动化三角高程也可以达到二等水准的精度。
3 结束语本文研究了基于机器人的精密三角高程自动化监测的主要误差来源,并通过采取一定的监测措施:通过保证视线高度,选择异午多时段、多测回,能够明显改善三角高程的精度;根据基准点间相对固定的距离和高差特点,利用自动化监测及差分技术可以明显提高测距、测角及高差的精度;采取基于强制对中装置观测墩的混合基准点网法,且控制视线长度,减少测角误差,仪器高站标高可忽略不计,通过试验数据计算及精度分析说明该自动化三角高程方法能达到二等水准精度,且效率大大提高,对多种类型监测工程具有借鉴和推广作用。
| [1] | 张正禄, 邓勇, 罗长林. 精密三角高程代替一等水准测量的研究[J]. 武汉大学学报·信息科学版, 2006, 31(1): 5–8 |
| [2] | 杨凤芸, 赵文, 刘玉梅. TM30三角高程代替二等水准测量的精度分析[J]. 沈阳建筑大学学报 (自然科学版), 2012, 28(4): 657–662 |
| [3] | 刘成龙, 杨雪峰, 张阅川. 基于测量机器人的二等高程控制测量新方法[J]. 西南交通大学学报, 2013, 48(1): 69–74 |
| [4] | 许国辉. 高精度EDM三角高程测量的研究[J]. 测绘通报, 2002, (10): 22–24 DOI: 10.3969/j.issn.0494-0911.2002.10.007 |
| [5] | 张正禄, 文鸿雁, 葛永慧, 等. 简明工程测量学[M]. 北京: 测绘出版社, 2014 |
| [6] | 黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2010 |
| [7] | 梅文胜, 杨红. 测量机器人开发与应用[M]. 武汉: 武汉大学出版社, 2011 |
| [8] | 卢凌燕, 卢松耀, 梁龙昌. 逆作法深基坑施工的变形监测方法研究及其应用[J]. 测绘地理信息, 2016, 41(3): 20–24 |
| [9] | 梅文胜, 张正禄, 郭际明, 等. 测量机器人变形监测软件系统研究[J]. 武汉大学学报·信息科学版, 2002, 27(2): 165–171 |
| [10] | 张正禄, 罗年学, 郭际明, 等. COSA_CODAPS及在精密控制测量数据处理中的应用[J]. 测绘信息与工程, 2010, 35(2): 52–54 |
 2017, Vol. 42
2017, Vol. 42

