| 基于ARIMA模型的ECMWF压强预测 |
研究掌握全球水汽变化的时空特性对于研究全球气候环境变化和改善气象预报水平具有重要的科学和现实意义。传统的水汽观测手段主要包括无线电探空仪、水汽辐射计等,存在着工作量大、设备昂贵、时空分辨率低等不足之处,已不能满足现代气象学发展的需要。随着GPS的发展,地基GPS反演水汽成为一种新的技术手段,具有实时性、精度高等优点。其主要原理是通过GPS精密单点定位计算得到的天顶湿延迟ZWD (zenith wet delay)与表征水汽变化的参数可降水量PWV[1](precipitable water vapor)之间的关系来反演水汽。
| $ {\rm{PWV}} = \mathit{\Pi } \cdot {\rm{ZWD}} $ | (1) |
式中,Π为水汽转换因子,现可经过计算得到精密值;ZWD可由如下公式计算:
| $ {\rm{ZTD}} = {\rm{ZWD}} + {\rm{ZHD}} $ | (2) |
其中,ZTD (zenith total delay)为对流层天顶总延迟,包括天顶干延迟ZHD (zenith hydrostatic delay)和天顶湿延迟ZWD两个部分。ZTD通过GPS单点定位可以精确获得,ZHD常用理论经验模型Saastamoinen模型[2](简称SA模型)进行计算。
| $ {\rm{ZHD}} = \frac{{\left( {2.2779 \pm 0.0024} \right){P_S}}}{{f\left( {\lambda, H} \right)}} $ | (3) |
其中,Ps为地表压强; f(λ, H)为与测站纬度λ和高程H有关的表达式。从公式(3)可以看出,压强是干延迟精度的主要决定因素。研究表明,10~15 hPa的气压精度可产生2~3 cm量级的干延迟,转换成水汽的精度误差约为5 mm。因此,通过地基GPS反演得到实时的高精度水汽,关键的一步是得到精确的压强。但是并不是所有的GPS测站都能获得实测压强值。目前, 全球各气象中心根据大量的气象观测和卫星反演资料,基于各种数学方法进行数值计算建立数值天气预报模型NMM (numerical weather models),也可以提供全球压强格网数据,具有时空分辨率高、精度高的优点,目前常用于科学研究的为欧洲中期天气预报中心ECMWF (european centre for medium-range weather forecasts),可提供空间分辨率为2.5°×2.5°、时间分辨率为6 h (UTC时06:00、12:00、18:00、24:00)的高精度地表压强值,能满足地基GPS反演水汽时压强的精度要求,但是该产品并非实时发布,因此不能满足实时性需求。由于其高精度和高时空分辨率,因此常被用于气象参数模型的建立和检验。
考虑到以上两种数据源均无法得到的情况,Boehm采用ECMWF提供的3年全球月平均压强和气温格网数据,基于9阶9次球谐函数建立了全球气压和温度经验模型GPT[3] (global pressure and temperature),通过测站坐标和年积日即可提供全球范围的气压和气温,使用简单方便,但是GPT模型只能反映压强的年变化特性,且时空分辨率低。Lagler等针对GPT模型和经验映射函数模型GMF[4] (global mapping function)的部分不足之处进行了改进和优化,从而构建了GPT的改进模型GPT2[5]。GPT2模型采用质量更高的数据进行建模,同时在经验模型表达式中加入了半年周期项并估计了各个周期项的初相,最后利用5°×5°的格网代替9阶9次球谐函数进行成果表达,提高了模型的空间分辨率。
压强由于受到诸多因素的影响,变化极其复杂。提取出ECMWF提供的2004年3天的压强时间序列进行分析,结果如图 1所示。从图中可以看出,大多数压强日周期具有两个波峰和波谷,日周期特性明显。GPT2只能反映压强的半年周期特性,整体精度不及ECMWF产品。
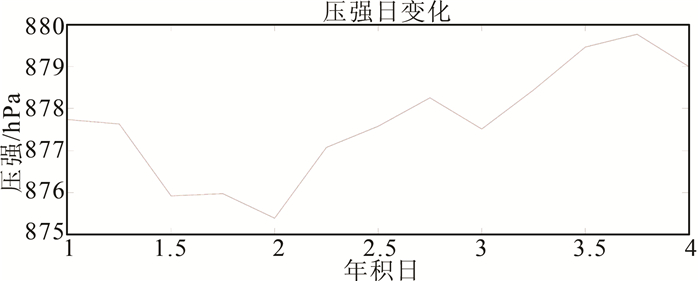 |
| 图 1 2004年年积日为1~4期间的压强时间序列图 Figure 1 Pressure Time Series in DoY of 1~4 in 2004 |
时间序列分析[6]是一种通过已有的序列揭示某一现象的发展变化规律并进行预测的方法。特别是ARIMA (auto-regressive integrate moving average)模型的发展为预测工作者们提供了科学系统的分析方法,目前已广泛应用于气象数据短期预报中。由于压强的变化受到诸多因素的影响,其既有长期趋势、季节效应,又具有随机扰动效应,将时间序列分析引入压强的预测研究中,利用压强序列的自身变化来获取压强预测值,不失为一种有效的方法。
本文基于ECMWF提供的高精度高、时空分辨率的压强值,采用时间序列分析的方法对已有压强序列进行ARIMA建模并预测,检验预测精度,结果表明,通过时间序列建模预测得到的压强值可以用来计算天顶干延迟,进而进行地基GPS反演水汽的计算。
1 ARIMA建模原理及方法时间序列分为平稳和非平稳序列两种[7],对于平稳序列,可以用ARMA (auto-regressive and moving average)模型进行建模,而现实中很多序列往往是非平稳的,若其经过d次差分可以得到一个平稳的ARMA过程,则称其为ARIMA (p,d,q)模型,其数学表达式为:
| $ {W_t} = {\varphi _1}{W_{t - 1}} + {\varphi _2}{W_{t - 2}} + \cdots + {\varphi _p}{W_{t - p}} + {e_t} - {\theta _1}{e_{t - 1}} - {\theta _2}{e_{t - 2}} - \cdots - {\theta _q}{e_{t - q}} $ | (4) |
| $ {W_t} = {\nabla ^d}{Y_t} $ | (5) |
其中,Wt表示原始数据Yt的d阶差分;p、q分别为自回归部分和滑动平均部分的阶数;φi(i=1,2,…,p)、θj(j=1,2,…,q)分别为自回归系数和滑动平均系数;{et}为白噪声序列。
ARIMA (p,d,q)建模的步骤为:①数据预处理。首先对将要研究的序列进行初步分析,判断其平稳性、独立性和正态性。常采用自相关系数图检验法,若为平稳序列,则具有白噪声特性,自相关函数应该逐渐趋向于零;否则为非平稳序列。对于非平稳序列,先经过差分,使其变成平稳序列。②模型阶数及参数估计。由样本自相关函数ACF图和偏自相关函数PACF图的截尾性和拖尾性并结合AIC或BIC最佳准则来确定模型的阶数。模型阶数初步估计后,对所建议的模型通过矩估计、最小二乘估计、条件最小二乘、极大似然估计等方法进行参数估计。③模型诊断。经过①、②步后,必须用数理统计的方法对模型的合理性进行检验,判断模型法是否能反映实际情况,并改进模型与实际的不符之处。常用方法是残差检验。若残差符合白噪声序列特性,服从标准正态分布,说明模型是合适的。④预测及分析[8]。
2 压强时间序列建模 2.1 数据来源及使用软件根据ECMWF提供的空间分辨率为2.5°×2.5°、时间分辨率为6 h的压强全球格网数据,取东经110°上N90°~S90°间隔为10°的18个格网点2001-2003年的数据分别进行ARIMA建模,并用2004年的数据进行预测精度检验。每个格网点的建模过程和结果基本一致。本文选取其中北纬40°、东经110°、大地高为1 254.5 m的格网点为例,压强序列个数为1 095 ×4,经过初步ARIMA模型估计,发现用原始数据建模,阶数较大,需要参数较多,可能会导致相关性的减弱,模型的不稳定性增加。经分析发现,压强日波动值一般在5 hPa以内,多数为2~3 hPa,有少数会出现8~10 hPa的波动,主要发生在三四月。因此,可以用日平均温度来作为测站温度用于天顶干延迟的计算。本文对原始数据进行日平均处理,得到2001-2003年共1 095个日平均数据,并对此序列用R语言进行ARIMA建模[9]。
2.2 数据预处理首先对原始序列进行平稳性分析。如图 2为2001-2003年日平均压强原始图,图 3为自相关函数图。
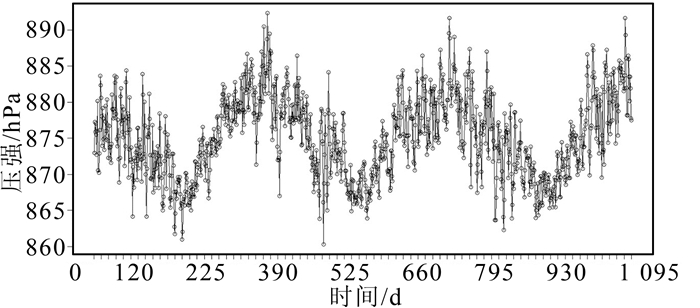 |
| 图 2 原始序列图 Figure 2 The Original Pressure Time Series |
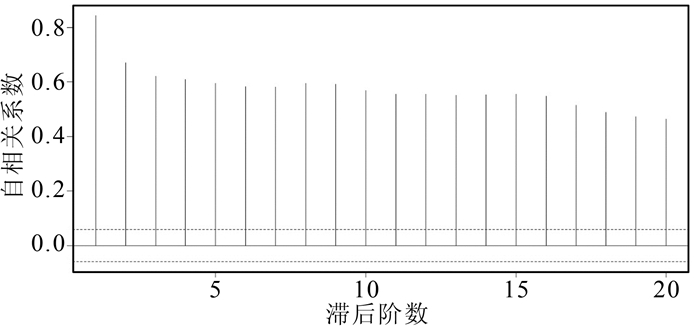 |
| 图 3 原始序列自相关函数图 Figure 3 ACF for the Original Pressure Time Series |
图 2表明该序列具有明显的周期性,图 3表明该序列的自相关系数不符合白噪声特性。因此,该序列为非平稳序列。对其进行一阶差分处理[10],得到差分后的时序如图 4所示;对差分后的序列进行自相关系数分析,得到其自相关函数图如图 5所示。
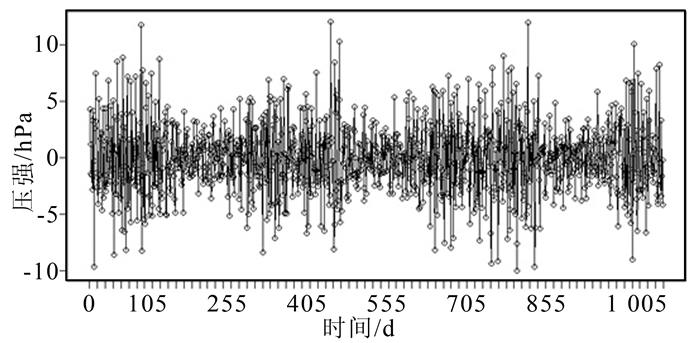 |
| 图 4 一阶差分图 Figure 4 First Difference |
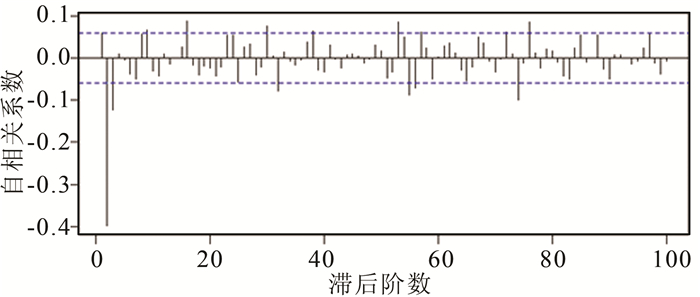 |
| 图 5 一阶差分后自相关函数图 Figure 5 ACF After First Difference |
从图 4、图 5可以看出,进行一阶差分后的时间序列图近似于平稳时间序列。
2.3 模型阶数及参数估计本文采用AIC最佳准则和BIC最佳准则[11-13]均得到最佳模型为ARIMA (1, 1, 1)。采用极大似然估计法,得到模型参数φ1=-0.470 5,θ1=0.695 3。因此,可得2001-2003年日平均压强的ARIMA (1, 1, 1)模型表达式为:
| $ {Y_t} - {Y_{t - {\rm{1}}}} = - {\rm{0}}{\rm{.4705}}\left( {{Y_{t - {\rm{1}}}} - {Y_{t - {\rm{2}}}}} \right) - {e_t} - {\rm{0}}{\rm{.6953}}{e_{t - {\rm{1}}}} $ | (6) |
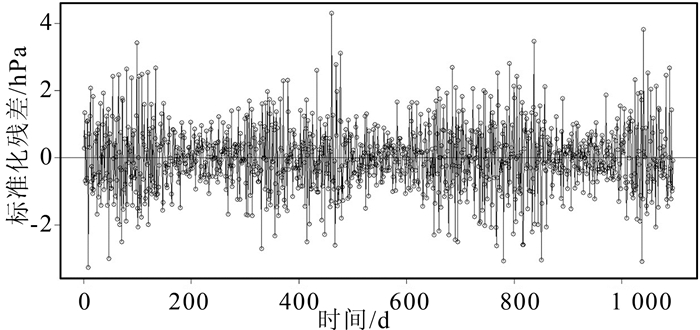 |
| 图 6 ARIMA (1, 1, 1)残差图 Figure 6 Residuals for ARIMA (1, 1, 1) |
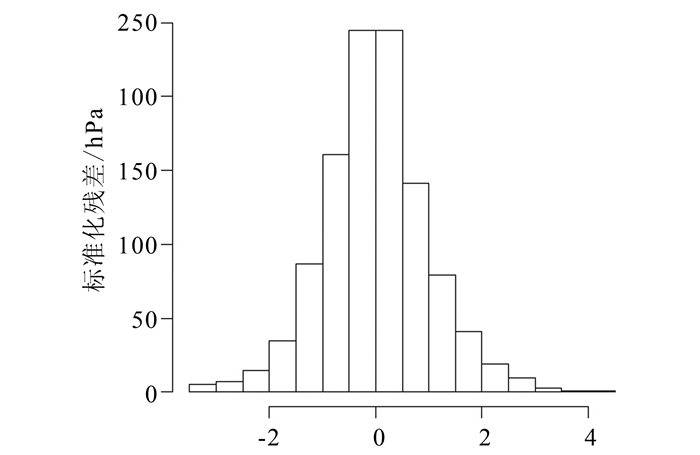 |
| 图 7 残差直方图 Figure 7 Residuals Histogram |
从图中可以看出,残差服从零均值正态分布,说明模型拟合较好。
3 模型精度检验 3.1 直接预测利用建立的模型进行10步预测,即预测未来10天的日平均压强值,结果如图 8所示。
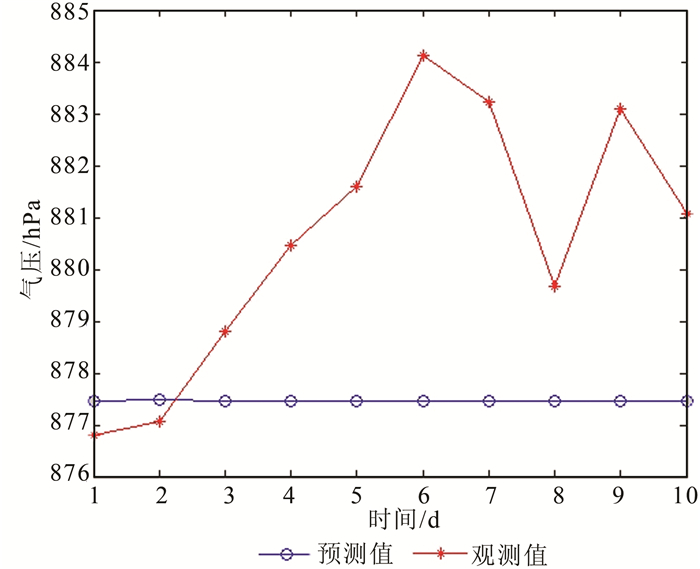 |
| 图 8 10步预测 Figure 8 Forecasts in 10 Days |
从图 8可以看出,3天以内精度在2 hPa以内,5天精度在5 hPa以内,随着时间的增加,预测精度越来越差,且不能显示压强的变化趋势。
3.2 更新预测利用2004年的日平均压强进行更新预测,每次在原始数据上增加一个数据预测下一天的日平均压强。首先进行20步更新预测,结果如图 9所示。
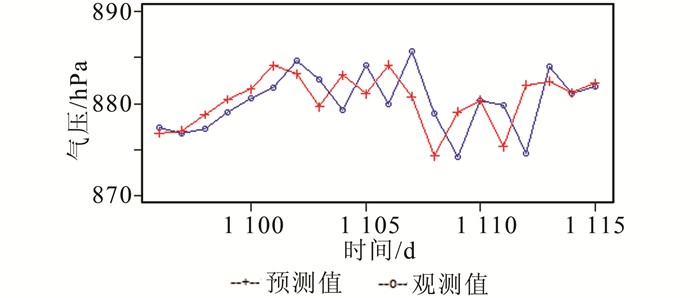 |
| 图 9 ARIMA (1, 1, 1)20步更新预测 Figure 9 Recursive Updating Forecasts in 20 Days |
从图 9可以看出,20步更新预测值精度很高,与原始值差值大多数不超过1 hPa,少数在1~2 hPa之间,说明用该更新预测法预测接下来一个月的日平均压强可以得到很高的精度。但是更新预测需要每次提供新的压强数据,在压强数据已知,只需要预测未来一天的情况下,采用更新预测方法可以得到很高的精度。当原始数据不够时,采用直接预测法,可以进行5天以内的短期预测,若要长期预测,还需要采用其他更精确的方法进行建模预测,或者直接采用GPT系列模型计算压强。
4 结束语压强是计算天顶干延迟的关键参数,基于实测压强值和通过数值天气预报模型NWM提供的参考压强值均无法得到的情况下,人们常采用全球经验模型GPT来计算压强,但是精度较低。本文采用时间序列分析方法,基于ECMWF提供的高精度压强时间序列值提出了可用于压强预测的ARIMA (1,1,1)模型,预测结果精度较高,能满足水汽计算的精度要求,证明了该方法的可行性。但是本文仅针对18个格网点进行了ARIMA模型短期预测的实验,由于不同经纬度地区的压强变化特征不一样,同时压强还会受到高山、平原、海洋等地形的影响,因此不能用ARIMA模型对全球所有格网点建立统一的一个确定模型。在接下来的工作中,可以进一步用这种方法对每个格网点分别进行建模,以模型系数作为输出产品,建立一个全球服务系统,需要者只要输入经纬度,就可以得到具体的ARIMA模型。在未来,可以尝试通过引入季节因子等方法改进压强的时间序列建模方法,采用更高时间和空间分辨率的压强进行建模,同时考虑到压强的月变化、日周期变化等短时变化特性,加入新的参数,得到更为精确的模型。
| [1] |
陈俊勇. 地基GPS遥感大气水汽含量的误差分析[J].
测绘学报,1998,27(2) : 113–118.
Chen Junyong. On the Error Analysis for the Remote Sensing of Atmospheric Water Vapor by Ground Based GPS[J]. Acta Geodaetica et Cartographica Sinica,1998,27(2) : 113–118. |
| [2] | Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. The Use of Artificial Satellites for Geodesy,1972,15(1) : 247–251. |
| [3] | Boehm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy,2007,81(10) : 679–683. DOI:10.1007/s00190-007-0135-3 |
| [4] | Böhm J, Niell A, Tregoning P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters,2006,33(7) : . |
| [5] | Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters,2013,40(6) : 1069–1073. DOI:10.1002/grl.50288 |
| [6] |
杨叔子, 吴雅.
时间序列分析的工程应用: 上册[M]. 武汉: 华中科技大学出版社, 2007 .
Yang Shuzi, Wu Ya. The Engineering Application of Time Series Analysis: The First Volume[M]. Wuhan: Huazhong University of Science and Technology Press, 2007 . |
| [7] | Box G P E, Jenkis G M. Time Series Analysis, Forecasting and Control[M]. San Francisco: San Francisco Press, 1978 . |
| [8] | Cryer J D, Chan K S. Time Series Analysis with Applications in R[M]. Beijing: China Machine Press, 2011 . |
| [9] |
丛凌博, 蔡吉花. ARMA模型在哈尔滨气温预测中的应用[J].
数学的实践与认识,2012,42(16) : 190–195.
Cong Lingbo, Cai Jihua. The Application of Auto-Regressive and Moving Average Model in Harbin Temperature Forecast[J]. Mathematics in Practice and Theory,2012,42(16) : 190–195. |
| [10] |
石昱馨, 刘喜波. 乘积季节模型在气温及降水时间序列分析中的应用[J].
数学·力学·物理学·高新技术交叉研究进展,2010,(13) : 792–797.
Shi Yuxin, Liu Xibo. Seasonal Model of the Product in the Application of Temperatures and Precipitation Time-Series Analysis[J]. Mathematics, Mechanics, Physics, Advanced Technology Cross-over Research Progress,2010,(13) : 792–797. |
| [11] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J].
武汉大学学报·信息科学版,2011,36(3) : 267–270.
Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University,2011,36(3) : 267–270. |
| [12] |
贺小星, 花向红, 周世健. GPS时间序列中异常周期信号影响机制分析[J].
测绘地理信息,2014,39(2) : 22–26.
He Xiaoxing, Hua Xianghong, Zhou Shijian. The Effects Mechanism of Anomalous Period Signal in GPS Time Series[J]. Journal of Geomatics,2014,39(2) : 22–26. |
| [13] |
徐卫东, 伍锡锈, 欧海平. 基于时间序列分析和灰色理论的建筑物沉降预测模型研究[J].
测绘地理信息,2012,37(6) : 23–25.
Xu Weidong, Wu Xixiu, Ou Haiping. Research on Building Subsidence Prediction Model Based on Time Series Analysis and Grey Theory[J]. Journal of Geomatics,2012,37(6) : 23–25. |
 2016, Vol. 41
2016, Vol. 41

