| 工业近景摄影测量编码标志改进与识别算法研究 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Key Laboratory of Precise Engineering and Industry, National Administration of Surveying, Mapping and Geo-information, Wuhan 430079, China
对于大型工业设备的安装与检测,如飞机、电子对撞机、长直导轨等,工业近景摄影测量由于其精度和效率高,是一种理想的技术手段[1-3]。在工业摄影测量中或在一些被测物体没有明显特征的其他场景摄影测量中,编码标志必不可少,它不仅能够有效解决图像匹配过程中两幅图像对应点之间的关系问题,并且可以提高特征识别的准确性和精度[4, 5]。
目前主流的编码标志有两种,一种是环形编码标志;一种是点位编码标志[6-9]。环状编码标志点的识别算法比较简单,方便提取,但该类编码标志点容易受拍摄角度影响,引起误识别,且由于环带没有起始标志,编码容量较小。点状编码标志则是由一组规律排放的圆点组成,只有圆形特征,结构简单,并且点状编码标志自身带有坐标系,编码容量更大,识别稳定性更高,但点状编码标志在寻找定位点的过程中需要循环搜索编码点,算法较为复杂,解码速率不高;且点状编码标志的定位点大小与其他点一样,当定位点很小时会影响中心的确定从而导致定位精度不高。受到编码容量和定位精度的限制,目前这两种编码点都无法直接用作大型工业设备的监测点,无法实现大量测量点的自动管理。
为得到一种方便提取、编码容量大、受拍摄角度影响小且定位精度高的编码标志点,本文设计了一种由环形编码标志和圆点编码标志组成的编码标志点,设置了4个模板点,其作用既可以提高编码容量,又可以用来计算射影变换矩阵来对抗标志的透视变形,从而提高编码标志识别的准确率。而且这种编码点的定位精度高,可以直接用作大型工业设备的监测点。
1 编码标志设计及编码原则 1.1 编码标志设计工业数字摄影测量中的编码标志应具有足够的编码容量,从而满足不同尺寸的测量目标需求。尺寸不应过大,以免对测量目标造成遮挡。应易于自动、准确识别,因为它就是为了自动测量而存在的。应有唯一定位点,便于相片的定向和不同相片的像点匹配[10]。
本文遵循以上原则设计了如图 1所示的编码标志,该标志将环形编码标志与圆点编码标志结合,中间部分为一个8位的环形编码标志,最中间的最大的圆点是环形编码标志的定位点,也是整个编码标志的定位点。外圈是点状编码标志,4个角是4个模板点,两个同心圆的是一类模板点N0,也是编码标志坐标系的原点,另外3个为二类模板点,顺时针分别为N1、N2、N3。在相邻的两个模板点之间有3个编码点,共12个编码点,所以圆点编码的容量为212,加上中间的环带8个编码标志,总的编码容量为220, 即1 048 576。如果中间圆环选用10位,则编码容量可以达到222,如果中间圆环选用更多的位,编码容量可以更大,编码容量与中间圆环位数的关系如式(1)所示。
| $ C_{\text {apacity }}=2^{n_{-} \text {band }+n_{\text {_codedot }}} $ | (1) |
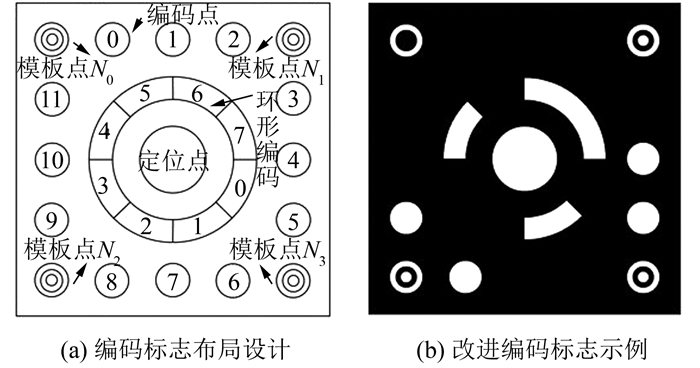 |
| 图 1 改进编码标志 Fig.1 Proposed Coded Marks |
式中,C是总的编码容量;n_band是环带的位数;n_codedot是编码圆点的个数。
1.2 编码规则按照前面所叙述的,新的编码标志由两部分组成,12个编码点的点分布标志和8位的环形编码标志,因此,编码也由两部分组成,分别为点分布标志码和环形码,如点分布码为110,环形码为212,那么总的编码为110-212。
如图 1(a)所示,点分布标志的编码点从0~11按顺时针排序,其编码规则为,当点位是白色时,该位的标识符为1,当点是黑色时,该位的标识符为0,点分布标志的编码按照式(2)来计算。
| $ C_{\mathrm{dot}}=\sum\limits_{i=0}^{11}\left(\mathrm{Flag}_{i} \cdot 2^{i}\right) $ | (2) |
式中,Cdot为点分布标志的编码;Flagi为第i个编码点的标识符,为0或者1。同样,环形标志的编码点如图 1(a)所示从0~7按照顺时针排序,其编码规则为,当环带中的该位是白色时,该位的标识符为1,当是黑色时,该位的标识符为0,环形标志的编码按照式(3)来计算。
| $ C_{\text {circular }}=\sum\limits_{j=0}^{7}\left(\text { Flag }_{j} \cdot 2^{j}\right) $ | (3) |
式中,Ccircular为环形标志的编码;Flagj为第j个编码点的标识符,为0或者1。因为环形编码编码最大为255,因此为了简便运算,总的编码可以按照式(4)来计算。
| $ C_{\text {new }}=C_{\text {dot }} \cdot 1000+C_{\text {circular }} $ | (4) |
式中,Cnew为新的编码点的编码。
以图 1(b)为例,其中圆点编码为白色的点为4、5、8、9,按照式(2)其圆点编码为816,环带上为白色的位为1、4、6、7,按照式(3)其环形标志编码为210,因此按照式(4)总的编码标志编码为816-210。
2 编码标志识别编码标志的识别是进行标志编码的逆过程,本文将介绍编码标志的识别原理和过程。
2.1 识别算法编码标志识别涉及的关键算法有二值化、轮廓提取圆识别和投影变换。
2.1.1 二值化图像二值化就是将图像上的像素点灰度值设置为0或255,其目的是最大限度地保留图像中感兴趣的部分,是必要的图像预处理过程[11]。对编码标志的识别首先要对编码标志进行二值化,以便后续判断编码圆点和环带位的占位情况以及其他操作。二值化的关键在于阈值的选取,最原始的阈值选取办法就是对整幅图像都用一个统一的阈值来进行二值化,如使用127作为阈值,则小于127的像素值设为0,大于等于127的像素值设为255,这种方法操作简便快速,如图 2(a)所示,但效果不佳。本文采用的二值化方法是最大类间差方法,其基本原理是找到一个阈值使前景与背景的方差最大,因为方差可以衡量灰度分布的均匀性,当前景与背景的分类正确时,图像两部分的差别是最大的[12]。如图 2(b)是最大类间差法的二值化结果,可以看到其很好地保留了细节。
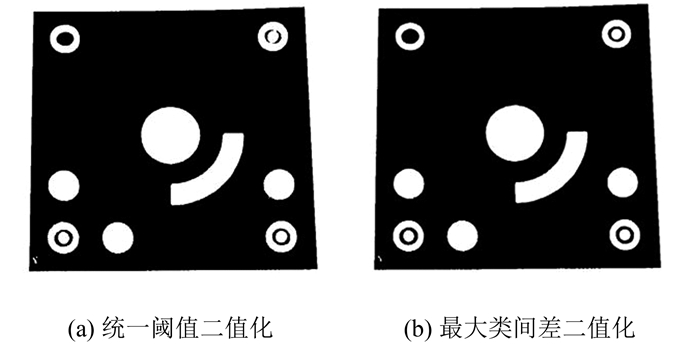 |
| 图 2 二值化处理结果对比 Fig.2 Comparison of Binarization Results |
2.1.2 轮廓检测提取
轮廓提取算法是数字图像处理的基本技术之一,本文采用的轮廓提取算法是Suzuki等[13]在1985年提出的对于二值影像的轮廓提取算法,其提取了一系列边界点的坐标或者链码。边界提取的结果如图 3所示。
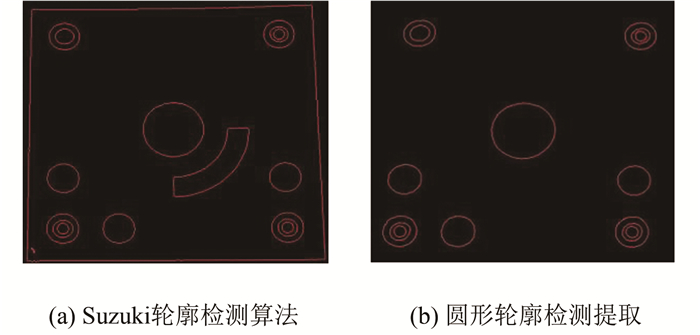 |
| 图 3 轮廓检测结果 Fig.3 Contour Detection Results |
2.1.3 圆形轮廓检测
该编码标志的点排列编码标志点和定位点都是圆形,因此,要进行圆形轮廓的检测。该检测方法利用了一个圆的性质,即圆的最小外接圆与其面积比例应近似为1[14]。而求取最小外接圆的方法是:要找到这样一个圆,轮廓上所有的点都在其圆形范围内,且没有面积更小的圆。其识别结果如图 3(b)所示。
2.1.4 投影变换相机拍摄的过程是中心投影的过程,在成像的过程中编码标志上的点会发生投影变换,摄影变换后不变的是线的相交关系和交比[15]。其变换关系表达为:
| $ \left[\begin{array}{lll} x^{\prime} & y^{\prime} & w^{\prime} \end{array}\right]=\left[\begin{array}{lll} u & v & w \end{array}\right]\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right] $ | (5) |
| $ \left\{\begin{array}{l} x=\frac{x^{\prime}}{w^{\prime}}=\frac{a_{11} u+a_{21} v+a_{31}}{a_{13} u+a_{23} v+a_{33}} \\ y=\frac{y^{\prime}}{w}=\frac{a_{12} u+a_{22} v+a_{32}}{a_{13} u+a_{23} v+a_{33}} \end{array}\right. $ | (6) |
式中,u、v是原始图像的坐标;x、y是变换后的图片坐标,其中,
对本文所提出的编码标志进行识别的主要过程包括高斯滤波二值化、寻找轮廓、筛选出圆轮廓、寻找模点和定位点、计算圆点编码、计算环形编码、计算总的编码、判断编码位置、在图中显示识别出的编码和点位。
在计算圆点编码时,考虑到在拍摄过程中编码标志会发生投影变形,为了消除其对编码识别的影响,首先需要根据模板点来计算摄影变换矩阵,再利用投影变换矩阵将编码点的设计坐标转换到影像中,即计算编码点在影像中的坐标,然后逐个判断编码点在影像中所对应位置的灰度值,灰度值为0对应为黑,灰度值为255则对应为白,最后确定该编码标志点的标识符是0还是1,从而计算圆点编码标志的编码值。
3 编码标志识别结果设计几组不同的实验用来验证本文所设计的编码标志和识别方法:①不同场景下的编码标志识别;②不同角度的编码标志识别;③检验使用定位点辅助编码标志中心位置确定的有效性。
以地面作为背景对编码标志进行识别,使用的编码标志大小为5 cm×5 cm,编码标志以任意旋转角被摆放在地面上,使用相机像素为3 648×2 736,识别结果如图 4所示,从图 4中可以看出,所有12个标志都被正确地识别出来了,说明了该编码标志和识别算法在简单场景下是可用的。
 |
| 图 4 简单场景下编码标志的识别结果 Fig.4 Recognition Result of the Coded Marks in Simple Scene |
以有其他标识的墙面作为背景对编码标志进行识别,验证编码标志识别的抗干扰能力。与在简单场景中相同,使用的编码标志大小为5 cm×5 cm,编码标志以任意旋转角贴在墙上,使用相机像素为3 648×2 736,识别结果如图 5所示,从图 5中可以看出,所有12个编码标志都被正确地识别出来了,说明了该编码标志和识别算法在具有其他标志的复杂场景下是可用的。而在实际应该中,现场也会有各种其他标志,初步验证了该标志在实际测量中应用的可行性。
 |
| 图 5 复杂场景下编码标志的识别结果 Fig.5 Recognition Result of the Coded Marks in Complex Scene |
拍摄角度会对编码标志的识别造成影响,为了验证本编码标志的抗摄影变换能力,分别从不同的角度对标志进行拍摄,拍摄角度分别近似为15°、30°、45°和60°,识别结果如图 6所示。大于60°的实验也做了,但是识别失败了,因为圆形变形太大,没有被成功识别。因此,使用本标志应注意拍摄角度应在0~60°之间,为了保证影像上所有编码标志都可以被识别,最好在0~45°度之间。
 |
| 图 6 不同拍摄角度的编码标志识别结果 Fig.6 Recognition Result of the Coded Marks from Different Shooting Angles |
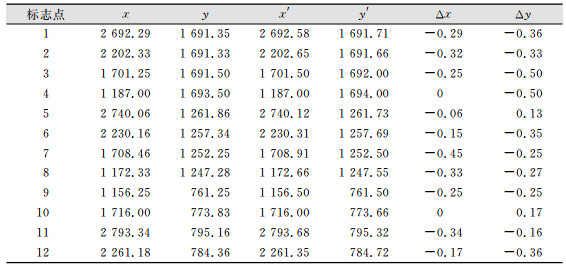
本文所使用标志的一个特别之处就是有4个模板点,这4个模板点可以用来帮助编码标志位置的精确确定[16-19]。为了验证其用于确定编码标志位置的效果,对排列整齐的3行4列的编码标志进行拍摄,对其进行识别并分别只用定位点和使用定位点和编码标志两种对其位置进行计算,识别结果如图 7所示。两种方法获得的标志点中心坐标如表 1所示,其中x, y为使用模板点计算的标志中心坐标,x′, y′为不使用编码点计算的圆心坐标, Δx和Δy为二者的差值。
 |
| 图 7 不同编码标志的识别结果 Fig.7 Recognition Results of the Coded Mark Array |
| 表 1 编码标志识别中心的坐标位置/像素 Tab.1 Coordinates of the Recognized Centers of the Coded Marks/pixels |
 |
虽然在拍摄过程中存在投影变形,但位于同一直线上的点在投影后依然在同一条直线上。利用这一性质对两种方法的定位精度进行评价,即计算在同一条直线上点的直线度,以直线度来衡量定位结果的好坏。直线度的计算方法为:将本应一条直线上的点中的起点和终点相连,计算中间的点到这条直线距离的平均值[20]。本实验中,编码标志的中心点共有7条直线,它们的直线度的解算结果如表 2所示。
| 表 2 直线度对比 Tab.2 Straight Line Deviation Comparing |
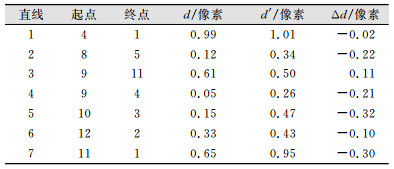 |
表 2中直线的起点和终点对应的点号如图 7所示。d为使用模板点的直线度,d′为不使用模板点的直线度,Δd为二者的差值。从表 2中可以看出,在7条直线中,有6条直线使用模板点参与定位的直线度均优于不使用模板点参与定位,最好的提高了0.32个像素。因此,可以得出结论:使用模板点可以在一定程度上提高定位精度。
4 结束语本文设计了一种新的编码标志,其特点是结合了环形编码标志和点位编码标志,并具有模板点。文章研究了编码标志的识别算法,包括二值化、边缘提取、圆轮廓提取、投影变换等,并实现了对编码标志的识别,实验表明该编码标志可以从0~45°被成功提取并且模板点的选择确实可以提高定位精度。
本文所设计的编码标志增加了编码标志的容量,提高了编码标志的定位精度,为工业摄影测量中编码标志使用提供了一个新的选择,但还有如下问题需要解决:
1) 可以选用更好的椭圆识别算法,来提高更大角度下编码标志的识别成功率;
2) 可以结合灰度加权质心法等进一步提高编码标志的定位精度;
3) 和数据库等技术结合,真正实现在大尺寸工业近景摄影测量中大量测量点的自动管理。
| [1] |
邹进贵, 孟丽媛. 近景摄影测量控制点快速自动识别与定位[J]. 测绘地理信息, 2018, 43(6): 70-73. |
| [2] |
孟祥丽, 刘瑶, 吴涛. 一种圆形编码标志点的设计及解码算法研究[J]. 传感器与微系统, 2018, 37(7): 42-44. |
| [3] |
孟祥丽, 陈聘, 丁华. 摄影测量中编码标志点设计方案概述[J]. 计量与测试技术, 2019, 46(1): 54-56. |
| [4] |
倪章松, 成垒, 顾艺, 等. 视觉测量中环形编码标志点的精确识别算法研究[J]. 新技术新工艺, 2016(12): 21-25. |
| [5] |
范生宏. 工业数字摄影测量中人工标志的研究与应用[D]. 郑州: 信息工程大学, 2006
|
| [6] |
Forbes K, Vougt A, Bodika N. An Inexpensive, Automatic and Accurate Camera Calibration Method[J]. Proceedings of the Thirteenth Annual South African Workshop on Pattern Recognition, 2002, 1-6. |
| [7] |
Ahn S J, Rauh W, Kim S I. Circular Coded Target for Automation of Optical 3D-Measurement and Camera Calibration[J]. International Journal of Pattern Recognition & Artificial Intelligence, 2001, 15(6): 905-919. |
| [8] |
Hattori S, Akimoto K, Fraser C, et al. Automated Procedures with Coded Targets in Industrial Vision Metrology[J]. Transactions of the Institute of Electronics Information & Communication Engineers, 2002, 84(5): 441-446. |
| [9] |
Chen R, Zhong K, Li Z, et al. An Accurate and Reliable Circular Coded Target Detection Algorithm for Vision Measurement[J]. Proceedings of the SPIE, 2016, 23: 1002319. |
| [10] |
Feng Q Q, Li Z C, Li G Y. Design and Decoding of Dot-Distribution Coded Targets[C]. 2010 8th World Congress on Intelligent Control and Automation, Intelligent Control and Automation (WCICA), Jinan, China, 2010
|
| [11] |
贾永红. 数字图像处理[M]. 第3版. 武汉: 武汉大学出版社, 2015.
|
| [12] |
Otsu N. A Threshold Selection Method from Gray-Level Histograms[J]. IEEE Transactions on Systems Man & Cybernetics, 2007, 9(1): 62-66. |
| [13] |
Suzuki S, Be K. Topological Structural Analysis of Digitized Binary Images by Border Following[J]. Computer Vision Graphics & Image Processing, 1985, 30(1): 32-46. |
| [14] |
Bradski G, Kaehler A. Learning OpenCV[M]. 1st ed. New York: O'Reilly Media, Inc., 2009.
|
| [15] |
Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M]. 2nd ed. England: Cambridge University Press, 2004.
|
| [16] |
戴相龙. 三维非接触式测量中编码标志的研究与应用[D]. 西安: 西安电子科技大学, 2014
|
| [17] |
冯文灏. 近景摄影测量的控制[J]. 武汉大学学报·信息科学版, 2000, 25(5): 453-458. |
| [18] |
龚小强, 邹进贵, 孟丽媛. 基于目标检测和角点检测的近景摄影测量控制点自动提取[J]. 测绘通报, 2020(S1): 173-175. |
| [19] |
田芮, 程效军, 李泉. 一种航空影像建筑物立面重复结构自动识别方法[J]. 测绘地理信息, 2018, 43(1): 104-108. |
| [20] |
Cai Z, Vasconcelos N. Cascade R-CNN: Delving into High Quality Object Detection[J]. Computer Vision and Pattern Recognition, 2017(6): 798-802. |
 2021, Vol. 46
2021, Vol. 46

