| 基于正弦定理的全站仪仪器高度测量方法的研究 |
全站仪三角高程测量作为高程测量的一种有效手段, 已被广泛应用于生产实践中[1]。尽管全站仪三角高程测量具有受地形影响较小、数据处理简单、测量效率高等优点[2],但同样受测量斜距、竖直角度、仪器高度以及大气折射等因素的影响[3],导致三角高程测量的精度较低,一般只是在普通工程测量或对高程精度要求不高的工程中运用。如何提高三角测量的精度,甚至代替高等级水准测量,一直是测量工作者们研究的热点课题之一。
三角高程测量是根据由测站向照准点所观测的高度角和两点间的斜距, 运用三角公式计算两点间的高差。根据三角高程测量的原理和误差传播定律,对如何提高精度,诸多学者做了大量研究。张正禄等[4]早在2006年就提出用精密三角高程代替一等水准测量;文献[5-10]对精密三角高程代替二等水准测量进行了研究与实践;文献[11-13]分析研究了全站仪三角高程测量代替三四等水准测量的可行性。
由三角高程测量原理可知,在不考虑大气折光和地球曲率时,影响三角高程测量精度的因素主要是垂直角、距离、仪器高和目标高。相关文献中,大多是对测量误差的分析改进及创新测量方法的研究,关于仪器高度测量方法的相关研究几乎没有。一些学者提出了一些不需要测量仪器高度的测量方法,如使用测量机器人在路线传递过程中进行偶数测边的对向观测,起、末点对中杆高度不变,避免了丈量仪器高和对中杆高带来的误差影响[7]。但这些方法需要特定的环境下、运用特定的仪器设备方可实现,而对于使用普通仪器的常规测绘工程(如道路工程的测设、基本比例尺地形图测绘等),可从量取仪器高度、提高观测精度等方向来提高三角高程测量精度。本文主要研究全站仪器高度测量方法,并进行精度分析,为三角高程测量的误差控制和高程测量的便捷性提供一定借鉴[2]。
1 仪器高度测量的现状分析目前全站仪高度一般都使用钢卷尺进行量取,测量员根据经验两次读数取平均值。如图 1所示,无论采取图 1中的哪种量测方式,量测仪器高度的误差都会较大。采取图 1(a)的方法,卷尺底端无法和桩点面在同一个水平面上,且无法保证卷尺的铅锤;采用图 1(b)的方法,仪器到桩点面是斜距,量取的数据误差更大。
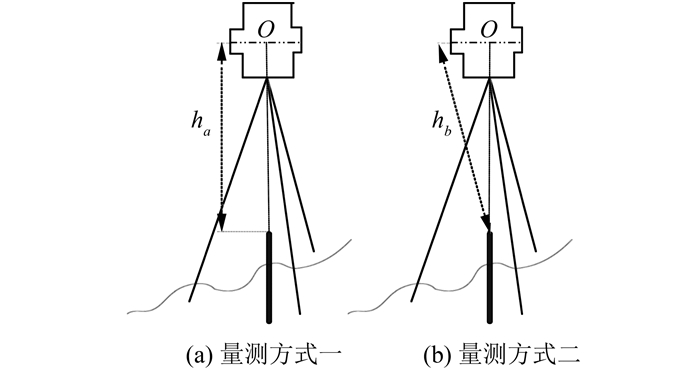 |
| 图 1 仪器高量测方式 Fig.1 Method of Measuring Instrument Height |
2 仪器高度测量方法及精度分析 2.1 仪器高度测量方法
基于三角高程测量的原理和正弦定理,提出了一种全站仪高度测量的新方法,这种方法简单便捷、无需专门的仪器设备。只需平时工程测量时常用的设备:全站仪、钢卷尺和带有圆水准器的强制对中杆(花杆)。
如图 2,在测站点A上架设全站仪,设全站仪中心点为O,距离A测站点1~2 m处架设强制对中杆(花杆),并调节圆水准器气泡使其居中,这时,强制对中杆(花杆)和全站仪竖轴处于平行状态,操作全站仪瞄准对中杆(花杆),并使其视准轴处于水平状态,指挥工作人员用铅笔在对中杆(花杆)划下全站仪水平视线的位置D点,全站仪向下瞄准C点(地面点),并做好记号,读出角度α,用钢卷尺量取AC的距离,同时量取CD边长,并做好记录。
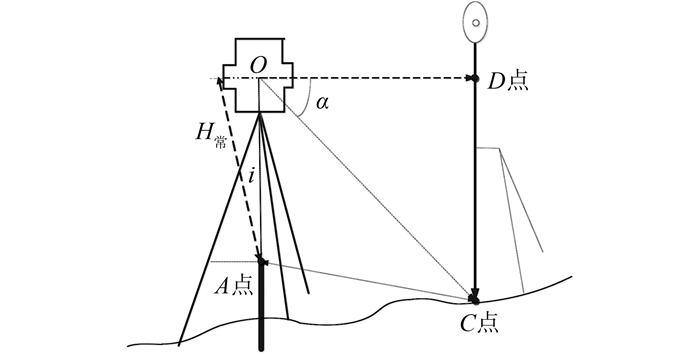 |
| 图 2 全站仪高度测量 Fig.2 Total Station Height Measurement |
其中,亦可事先在对中杆(花杆)做好刻度,或使用铟瓦尺,操作全站仪在刻度上读数。
根据正弦定理,显然:
| $ \begin{array}{*{20}{l}} {\frac{{AC}}{{\sin \left( {{{90}^\circ } - \alpha } \right)}} = \frac{{OC}}{{\sin \angle OAC}} = }\\ {\frac{{OA}}{{\sin \left( {{{180}^\circ } - \angle OAC - {{90}^\circ } + \alpha } \right)}}} \end{array} $ | (1) |
即:
| $ \frac{{AC}}{{\cos \alpha }} = \frac{{OC}}{{\sin \angle OAC}} = \frac{{OA}}{{\cos (\angle OAC - \alpha )}} $ | (2) |
通过量取AC、CD长度,读取α,可求得:
| $ \sin \angle OAC = \frac{{OC \times \cos \alpha }}{{AC}} = \frac{{\frac{{CD}}{{\sin \alpha }} \times \cos \alpha }}{{AC}} = \frac{{CD}}{{AC}} \times \cot \alpha $ | (3) |
根据式(2)可求:
| $ \begin{array}{*{20}{c}} {OA = \frac{{OC \times \cos (\angle OAC - \alpha )}}{{\sin \angle OAC}} = }\\ {\frac{{AC \times \cos (\angle OAC - \alpha )}}{{\cos \alpha }} = i} \end{array} $ | (4) |
这样就可求得全站仪的仪器高i。
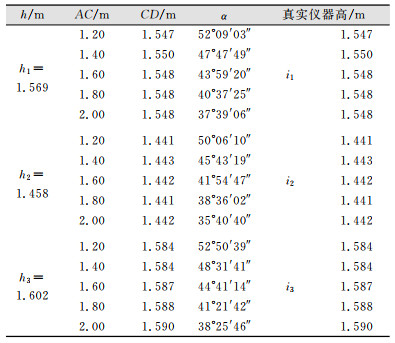
2.2 实验按照上述测量方法和实验原理,本文在实地摆设强制对中杆和全站仪进行了三组仪器高、距离不等的实验,每一组实验进行5次样本采集。根据正弦定理,结合式(4),得出了相应的仪器高(应注意的是:在计算式(3)时将会出现两个∠OAC,且它们互补为180°,但实际只可能是其中的一个值,故在外业摆放仪器时,应控制强制对中杆底端与测站点的高差在10~20 cm之间,不可太大亦不可太小),具体实验结果见表 1。其中h1、h2、h3代表传统方法量取的仪器高度,i1、i2、i3代表通过相关计算得出的真实仪器高。当然,在实际工作中除了使用强制对中杆(花杆),亦可使用经检校过的塔尺或铟瓦尺。
| 表 1 全站仪高度测量实验 Tab.1 Total Station Height Measurement Experiment |
 |
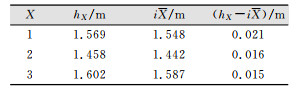
为了验证这种方法的精度,按传统的仪器高度量取方法(图 1(b))量取仪器高进行比较,见表 2。
| 表 2 新方法与传统方法量取仪器高度对比表 Tab.2 Comparision of New Method and Traditional Method to Measure Instrument Height |
 |
2.3 精度分析
从表 2可以看出,用传统的仪器高度量取方法量取仪器高与基于正弦定理求取的仪器高相比,均超了1~2 cm左右。若用传统的仪器高度量取方法量取仪器高,在很多精度要求较高的工程中,精度难以保证。
基于正弦定理的全站仪高度测量误差主要有仪器、钢卷尺、强制对中杆(花杆)或铟瓦尺、大气折光和地球曲率等误差。
1) 大气折光和地球曲率。由于全站仪竖轴和强制对中杆(花杆)之间的距离为2 m以内,参考文献[14]中的大气折光和地球曲率误差的计算公式, 这两种误差在本测量方法中可以忽略不计。
2) 仪器指标差。由于全站仪望远镜视准轴不水平或仪器竖轴不铅垂所造成的误差,经过检校合格的全站仪,指标差小于2″,对仪器高度测量的影响微不足道。
3) 钢卷尺误差。钢卷尺的精度直接影响到本测量方法的精度,故使用精度高的卷尺是提高精度的重要途径。
4) 强制对中杆的误差。强制对中杆带有圆水准器,误差主要是圆水准器的居中误差。根据测量实际经验以及参考当前研究成果,只要严格保证圆水准器的气泡严格居中,这个误差就很小,对本方法的测量结果的影响可以忽略不计。
3 结束语本文方法利用全站仪视准轴和强制对中杆在空间围合一个平面三角形,通过正弦定理计算出其余内角角度和各边边长,从而得到全站仪仪器高度。这个方法所需的仪器设备少,操作简单便捷,计算原理清晰,不受地形条件的限制,通过实验可知这种方法得出的全站仪仪器高度精度高。
同时,技术人员可根据自身情况,利用C++、C#或VB编写运算程序,并将其安装于全站仪或数据处理器中。这样,只需要将相应的数据输入就可以高效地求取出高精度的全站仪仪器高。
本方法可广泛应用于一般的地形测量、道路测设等工程测量,尤其是针对一些机箱较大的测量仪器,可有效提高三角高程测量的精度。
| [1] |
王慧超. 全站仪三角高程测量方法比较分析[J]. 测绘与空间地理信息, 2010, 33(2): 229-231. |
| [2] |
吕海波, 董均贵, 吴畏. 一种测量全站仪仪器高度的简便方法[J]. 测绘通报, 2017(5): 85-87. |
| [3] |
吕海波, 董均贵, 吴畏. 全站仪仪器高度测量新方法[J]. 测绘工程, 2017, 26(12): 38-40. |
| [4] |
张正禄, 邓勇, 罗长林, 等. 精密三角高程代替一等水准测量的研究[J]. 武汉大学学报·信息科学版, 2006, 31(1): 5-8. |
| [5] |
贾中甫, 杨郁, 冯启俊. 精密三角高程代替二等水准测量的研究与实践[J]. 测绘信息与工程, 2012, 37(1): 15-17. |
| [6] |
郭春喜, 阳海峰. 精密三角高程替代二等水准的可行性研究[J]. 测绘信息与工程, 2010, 35(2): 42-43. |
| [7] |
孔宁, 林鸿, 欧海平, 等. 基于自动照准全站仪的精密三角高程测量代替二等水准测量的研究与应用[J]. 测绘通报, 2016(2): 107-109. |
| [8] |
李凯, 石力, 朱清海. 应用精密三角高程测量替代二等水准测量[J]. 城市勘测, 2012(5): 89-93. |
| [9] |
田峰亮, 祝方才, 曹伟军. 全站仪三角高程测量与四等水准测量的精度比较分析[J]. 湖南工业大学学报, 2011, 25(3): 82-85. |
| [10] |
晏红波, 黄腾, 邓标. 智能全站仪精密三角高程测量替代二等水准测量[J]. 水电自动化与大坝监测, 2007(4): 43-47. |
| [11] |
陈喜麟, 柳建勇, 齐向威. 全站仪三角高程代替四等水准测量的探讨[J]. 包钢科技, 2007(4): 45-47. |
| [12] |
靳海亮, 赵长胜, 韩奎峰. 全站仪三角高程替代四等水准测量精度分析[J]. 辽宁工程技术大学学报, 2004(5): 606-608. |
| [13] |
汪耀武, 方梅. 全站仪三角高程测量代替三四等水准测量分析研究[J]. 武汉理工大学学报(交通科学与工程版), 2014, 38(6): 1413-1416. |
| [14] |
陈虎, 郑红晓, 李真真. 全站仪三角高程测量替代水准测量的精度分析[J]. 太原科技, 2009(10): 92-93. |
 2020, Vol. 45
2020, Vol. 45


