| 基于改进的CLAMBDA算法的低成本车载定姿研究 |
准确地确定整周模糊度是载波相位高精度定姿的关键。通常运用最小二乘模糊度降相关平差(least square ambiguity decorrelation adjustment, LAMBDA)方法来进行模糊度固定[1, 2]。在消费级车载姿态解算中,一般采用低成本GNSS接收机,载波观测值的频繁周跳以及伪距观测值的多路径影响使得采用LAMBDA方法进行整周模糊度固定时搜索成功率较低。为此,本文采用带约束的最小二乘模糊度降相关平差法(constrained LAMBDA, CLAMBDA)进一步提高模糊度固定的成功率[3, 4],即在LAMBDA方法的基础上增加一个基线约束;同时为处理频繁的周跳和失锁问题,采用单频单历元姿态解算方法[5-7];最后,由于CLAMBDA算法没有检核条件,且低成本接收机存在大量错误固定的情况[8, 9],本文提出了车载情况下的检验条件以提高姿态算法的性能,并进行具体的车载实验来进行测试和数据分析。
1 改进的CLAMBDA算法原理 1.1 CLAMBDA模型利用已知基线长度来强化GNSS模型。添加约束||b||=l,其中l为已知基线长度。于是标准GNSS模型扩展为:
| $ \begin{gathered} \mathit{\boldsymbol{E}}(y)=\mathit{\boldsymbol{A}} a+\mathit{\boldsymbol{B}} b, \mathit{\boldsymbol{D}}(y)=\mathit{\boldsymbol{Q}}_{y y}, \\ \quad a \in Z^n, b \in R^p,\|b\|=l \end{gathered} $ | (1) |
式中,E、D分别表示方差和期望;a为n阶的模糊度参数;b为p阶的位置坐标参数;l为基线长;A和B为给定的设计矩阵。
最小化问题变为二次型约束整数最小二乘(quadratic constraint integer least square, QC-ILS)问题
| $ \left\{ \begin{gathered} \check{a}\arg \mathop {\min }\limits_{a \in {Z^n}} \left( {\left\| {\hat a - a_{{Q_{\hat a\hat a}}}^2} \right\| + \left\| {\hat b(a) - \check{b}} \right\|Q_{{Q_{\hat b(a)\hat b(a)}}}^2} \right), \hfill \\ \hfill \\ \check{b}=\check{b}(\check{a}) \end{gathered} \right. $ | (2) |
式中,
| $ F(a) = \left\| {\hat a - a} \right\|_{{Q_{\hat a\hat a}}}^2 + \left\| {\hat b(a) - \check{b} (a)} \right\|_{{Q_{\hat b(a)\hat b(a)}}}^2 $ | (3) |
这样,F(a)就综合考虑了模糊度浮点解
在实际车载姿态解算中,基线长是事先测量的,所以有:
| $ \left\{\begin{array}{c} \mathit{\boldsymbol{E}}(y)=\mathit{\boldsymbol{A}} a+\mathit{\boldsymbol{B}} b, \mathit{\boldsymbol{D}}(y)=\boldsymbol{Q}_{y y}, a \in Z^n \\ \mathit{\boldsymbol{E}}(l)=\|b\|, \mathit{\boldsymbol{D}}(l)=\sigma_l^2, b \in R^p \end{array}\right. $ | (4) |
问题解为:
| $ \left\{\begin{array}{l} \check{a}=\arg \min\limits_{a \in Z^{n}} F(a) \\ \check{b}=\arg \min\limits_{b \in R^p} \mathit{\boldsymbol{H}}(\check{a}, b) \end{array}\right. $ | (5) |
其中:
| $ F(a)=\|\hat{a}-a\|_{Q_{\hat a\hat a}}^2+\min\limits_{b \in R^p} \mathit{\boldsymbol{H}}(a, b) $ | (6) |
| $ \mathit{\boldsymbol{H}}(a,b) = \left\| {\hat b(a) - b} \right\|_{{Q_{\hat b(a)\hat b(a)}}}^2 + \sigma _l^{ - 2}{(l - \left\| b \right\|)^2} $ | (7) |
由于附加基线条件,该目标函数不再适用于椭球搜索的方法。CLAMBDA主要的搜索方式根据GNSS模型强度、基线长度和条件基线精度等分为4种[10]。因为低成本车载实验中接收机较差,所以GNSS模型不强;又因为车顶长度有限,所以基线长度也不足;但因为约束基线方差矩阵近似于对角阵,所以可得近似约束整数最小二乘模糊度解为:
| $ \check{a}=\arg \min\limits_{a \in Z^n}\left(\|\hat a- a\|_{Q_{{\hat a\hat a}}}^2+\frac{\lambda}{1+\sigma_l^2 \lambda}(l-\|\hat{b}(a)\|)^2\right) $ | (8) |
式中,σl表示已知基线长的测量精度;
这种近似的优点是对基线长度没有任何限制,所以低成本车载定姿中采用该方法来进行CLAMBDA模糊度搜索。
1.3 检核条件在LAMBDA算法中是根据Ratio阈值判断整周模糊度是否固定成功,但CLAMBDA算法中因为要同时满足基线向量二次型和模糊度参数最小故不能根据Ratio值来判断,所以本身没有检核条件。由于低成本接收机在姿态解算的过程中存在大量错误固定的情况,因而有必要在CLAMBDA整周模糊度搜索过程中添加检核条件以提高姿态算法的性能。
本文提出两个低成本车载姿态解算中检验条件。首先是基线长检验,在实际车载定姿中,可以先验地确定一条或多条基线向量的定长,所以当模糊度整数值满足先验基线长要求时,初步认为是所求的模糊度固定值;其次可以利用车辆最大俯仰角检验,根据《城市道路工程设计规范》,正常路面有坡度要求。地面坡度不小于0.2%,通常不大于8%,部分路面经论证可增大到10%。所以,可以继续改进算法检核条件,加入最大俯仰角检验,以10%为阈值,来检核改进的CLAMBDA算法整周模糊度固定正确性。
1.4 算法流程CLAMBDA的算法流程如图 1所示。
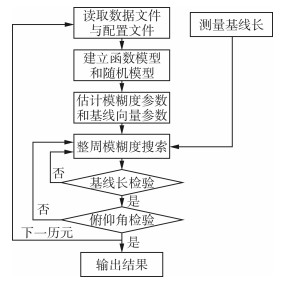 |
| 图 1 算法流程图 Fig.1 Flow Chart of Algorithm |
2 算例实验与分析
本文采用一组环境良好时的静态超短基线数据和动态车载超短基线数据,以及一组环境较差时的静态短基线数据和动态车载短基线数据进行测试分析,分别采用LAMBDA算法和本文提出的CLAMBDA算法进行单频单历元的解算,并统计各自的整周模糊度固定成功率及正确率。
测试天线采用低成本贴片天线,因为是低成本接收机,所以精度较差。首先于开阔环境下测试低成本接收机的性能及精度,整理数据绘制C/N0的累积分布函数(cumulative distribution function, CDF)图像以及双差残差图像如图 2、图 3所示。
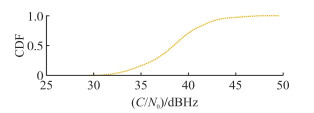 |
| 图 2 接收机载噪比 Fig.2 The Carrier/Noise of Receiver |
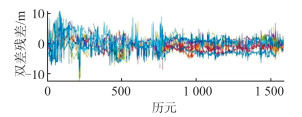 |
| 图 3 双差残差 Fig.3 Double Difference Residuals |
由载噪比CDF图像可见,C/N0值有65%位于30~40 d BHz之间,而在40 d BHz以上只有35%;其次由双差残差图像可以看出,该低成本接收机双差残差较大,总体上均值在5 m左右,当观测条件特别差时双差残差会增大到10 m以上,由此得知该低成本接收机性能较差。除此之外,由于载波观测值的频繁周跳以及伪距观测值的多路径影响会导致采用LAMBDA方法进行模糊度时搜索成功率变低。下面分别进行两组实验,验证不同条件下,LAMBDA算法与本文提出的改进的CLAMBDA算法整周模糊度固定性能。
第一组为环境良好时的数据,实验时间为2020年1月14日,地点为武汉市九峰山附近光谷七路,测试地点周边环境视野开阔遮挡较少,数据质量较高。基线长1 m,采样率1 s,静态实验共900个历元,动态实验共1 100个历元,采用GPS/BDS单历元单频观测数据,卫星截止高度角设为10°。
第二组为环境较差时的数据,实验时间为2019年11月26日,地点为武汉大学附近八一路,测试地点周边环境视野较差,遮挡严重,数据质量较差。基线长1.374 m,采样率1 s,静态实验共1 200个历元,动态实验共1 700个历元,采用GPS/BDS单历元单频观测数据,卫星截止高度角设为10°。
对上述实验数据分别利用LAMBDA方法和改进的CLAMBDA方法进行解算。采用LAMBDA算法时Ratio阈值设为3。统计实验整周模糊度固定成功率及正确率,如表 1和图 4、图 5所示。
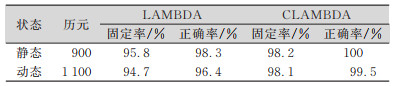
| 表 1 第一组实验:开阔环境 Tab.1 The First Group of Experiments: Open Environment |
 |
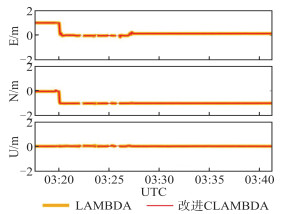 |
| 图 4 开阔环境静态实验结果 Fig.4 Results of Static Experiment in Open Environment |
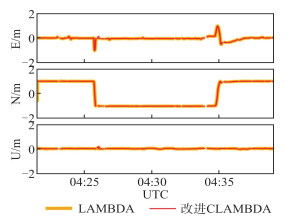 |
| 图 5 开阔环境动态实验结果 Fig.5 Results of Kinematic Experiment in Open Environment |
其中图 4为开阔环境下的静态实验,在开始时车辆进行了转向,后续保持静止;图 5为开阔环境下动态实验,车辆进行了往返运动。统计第二组实验整周模糊度固定成功率及正确率,实验数据及图像如表 2和图 6、图 7所示。
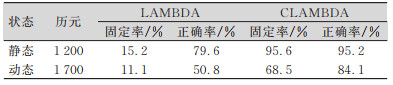
| 表 2 第二组实验:遮挡环境 Tab.2 The Second Group of Experiments: Occluded Environment |
 |
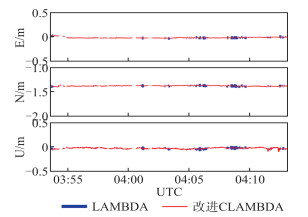 |
| 图 6 遮挡环境静态实验结果 Fig.6 Results of Static Experiment in Occluded Environment |
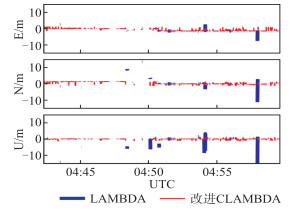 |
| 图 7 遮挡环境动态实验结果 Fig.7 Results of Kinematic Experiment in Occluded Environment |
从两组实验可以看出,静态数据的整周模糊度固定成功率均高于动态数据。因为第一组数据环境良好,第二组数据被遮挡严重,图形结构差、观测值噪声等误差影响较大,所以第一组的静态、动态数据结果均好于第二组。此外,两组实验中,改进的CLAMBDA算法整周模糊度固定成功率均好于LAMBDA算法,并且观测条件不好时效果更显著;动态实验比静态实验更明显。
第一组实验中,因为观测条件良好,静态实验时两种算法整周模糊度固定成功率都高于95%, LAMBDA算法为95.8%,改进的CLAMBDA算法为98.2%;动态实验时LAMBDA算法固定成功率为94.7%, CLAMBDA算法固定成功率为98.1%。CLAMBDA算法结果均好于LAMBDA算法,但差别并不明显。
第二组实验中,实验场地被遮挡严重,动态实验时LAMBDA算法成功率仅11.1%,静态实验时的算法成功率也仅15.2%;而CLAMBDA算法,动态实验时固定成功率提高到68.5%,静态实验时固定成功率提高到95.6%,改善效果明显。
无论哪组实验,改进的CLAMBDA算法的固定正确率都比LAMBDA方法高。环境良好时CLAMBDA算法能提高到99.9%以上。观测环境较差时,尤其是动态实验时,改进的CLAMBDA算法固定正确率比LAMBDA算法提高了30%左右,达到了84%以上,静态实验时能提升到95%以上。由此可见,改进的CLAMBDA算法整周模糊度的固定性能比传统LAMBDA算法性能更优越,尤其是在动态情况下,或观测环境较差时,改善效果更为明显。
3 结束语在实际低成本车载定姿实验中,因为低成本天线精度较差,很难得出满意的结果。这时可以先验确定基线向量长度。采用带有基线长约束的CLAMBDA方法,并添加验核条件,可以明显提高整周模糊度固定成功率与正确率。实验证明,本文提出的改进CLAMBDA算法优于传统方法,可以满足低成本GNSS接收机的车载姿态应用需求。
| [1] |
Teunissen P J G. On the GPS Double-Difference Ambiguities and Their Partial Search Spaces[C]. Geodetic Theory Today, Rio de Janeiro, Brazil, 1995.
|
| [2] |
Chang X W, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565. DOI:10.1007/s00190-005-0004-x |
| [3] |
单频BDS/GPS测姿算法研究与结果对比分析[J]. 测绘地理信息, 2015, 40(5): 17-20. |
| [4] |
Teunissen P J G. The LAMBDA Method for the GNSS Compass[J]. Artificial Satellites, 2006, 41(3): 89-103. |
| [5] |
附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报·信息科学版, 2005, 30(5): 444-446. |
| [6] |
一种附约束的单频单历元GPS双差相位解算方法[J]. 测绘学报, 2002, 31(4): 300-304. DOI:10.3321/j.issn:1001-1595.2002.04.004 |
| [7] |
GPS单历元定向和测姿算法及其精度分析[J]. 武汉大学学报·信息科学版, 2003, 28(6): 732-735. |
| [8] |
Nadarajah N, Teunissen P J G, Raziq N. Instantaneous BeiDou–GPS Attitude Determination: A Performance Analysis[J]. Advances in Space Research, 2014, 54(5): 851-862. DOI:10.1016/j.asr.2013.08.030 |
| [9] |
附有长度约束的模糊度解算方法比较[J]. 测绘科学, 2016, 41(6): 53-58. |
| [10] |
Teunissen P J G. Integer Least-Squares Theory for the GNSS Compass[J]. Journal of Geodesy, 2010, 84(7): 433-447. |
 2022, Vol. 47
2022, Vol. 47


