| 基于几何完整性的OSM面状要素位置精度分析及试验 |
2007年Good等[1]提出自发地理信息(volunteered geographic information, VGI),其中最具代表性的OSM(OpenStreetMap)地图数据被广泛使用,但由于OSM这类自发地理信息大多由非专业人员业余提供,其数据质量问题近年来受到了越来越多的关注。
多种不同的OSM地图数据质量检测方法被提出,但其研究重点主要集中在点和线状要素的完整度和位置精度[2-5],对面状要素的研究较少,且并未涉及位置精度[6]。地理位置信息对现实世界意义重大,OSM地图数据的免费性、开放性以及现势性等特点而被广泛应用,文献[2-5]研究了OSM数据点和线要素位置精度和完整性检验方法。而在现实生活中,OSM数据已经被用来寻址[7]和进行基于位置的服务[8],面状要素作为OSM地图的重要组成部分,对其位置精度的检验势在必行,但目前尚未有相关的检验方法。几何学中通常使用单一算法计算面状要素间的距离[9, 10],OSM数据生产的不规范性和自身的复杂性,使得单一方法并不能确定其面状要素间的距离。几何完整性较差的面状要素,基本上不具备位置精度,本文基于面状要素的几何完整性,提出了综合使用中心点距离法、双向面积重叠度和中心点距离相似度的方法,对OSM中面状要素的位置精度进行初步检验。
1 OSM面状要素位置精度分析方法OSM数据大多由非专业人员采集,无论是完整性还是位置精度都较低。OSM数据的生产方式不能保证完整性较好的面状要素具有较高的位置精度(图 1),本文主要针对具有较好完整性的OSM面状要素进行位置精度分析。
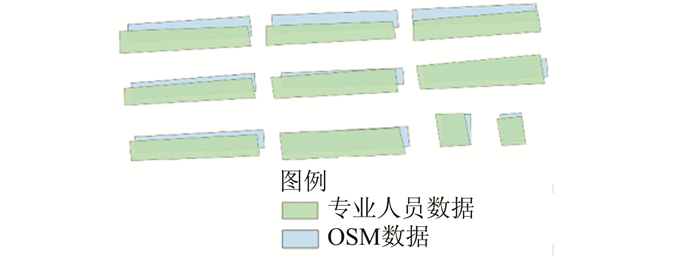 |
| 图 1 研究对象示例图 Fig.1 Samples of Research Elements |
本文对OSM面状要素位置精度分析主要包含两个方面:①OSM面状要素相对于专业人员获取的面状要素的几何完整性分析;②几何完整性较好的OSM面状要素的位置精度分析。主要使用对比方法,以OSM数据为测试数据,专业人员获取的数据为参考数据。
1.1 数据分类对比分析参考数据和测试数据,将面状要素分为以下7类:①Ⅰ类:参考数据和测试数据中都存在,在两类数据中均为独立个体且外形相似的面状要素;②Ⅱ类:测试数据中存在,但参考数据中不存在的面状要素;③Ⅲ类:测试数据中不存在,但参考数据中存在的面状要素;④Ⅳ类:测试数据中以单要素形式存在,但在参考数据中分片的面状要素;⑤Ⅴ类:参考数据中以单要素形式存在,但在测试数据中分片的面状要素;⑥Ⅵ类:在测试数据和参考数据中都是分片的面状要素;⑦Ⅶ类:在测试数据和参考数据中都是独立的个体,但是外观差别很大的面状要素(图 2)。
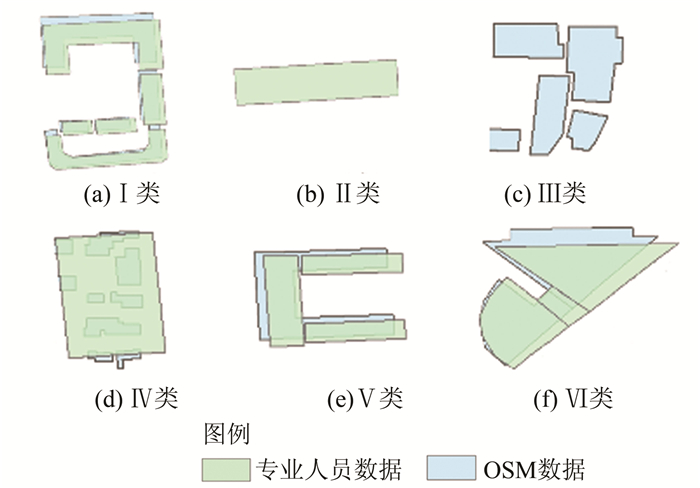 |
| 图 2 面状要素分类图 Fig.2 Classification of Planar Elements |
从图 2中可以看出,Ⅱ、Ⅲ、Ⅶ类不具备研究意义,Ⅵ可分解为Ⅰ、Ⅳ、Ⅴ三类,故本文以Ⅰ、Ⅳ、Ⅴ类面状要素为研究对象分析OSM面状要素的位置精度。
1.2 完整性检验方法测试数据中面状要素的几何完整性可以通过与参考数据中面状要素的相似性进行度量,相似性度量包含面积相似度、周长相似度和方向相似度3个方面[11],面状要素无较大形变和扭曲时,方向相似性可不作考虑,因而本文主要从面积相似度和周长相似度两个方面进行相似性度量。
1) 相似性度量方法。参考数据中某一面状要素的面积和周长分别为Sre和fPref,相应的测试数据中该面状要素的面积和周长分别为Sosm和Posm。
对于面积,面积相似度为:
| $ {S_A} = {S_{{\rm{osm}}}}/{S_{{\rm{ref}}}} $ | (1) |
对于周长,周长相似度为:
| $ {S_L} = {P_{{\rm{osm}}}}/{P_{{\rm{ref}}}} $ | (2) |
整体相似度S为:
| $ S = {S_A} \times {K_1} + {S_L} \times {K_2} $ | (3) |
式中,K1+K2=1。本文认为面积和周长同等重要,所以K1=K2=0.5。
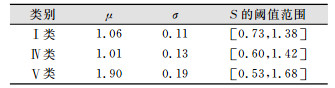
2) 完整性阈值的设定。根据相似度S的平均值μ和中误差σ,合理设置各类数据完整性检验的阈值。
1.3 位置精度分析方法参考数据和测试数据中同一面状要素的形状和顶点个数均有不同,中心点距离法计算的距离并不能代表所有顶点间的距离,因而不能作为面状要素间的距离。双向面积重叠度可以在一定程度上反映面状要素的分布情况和几何完整性,双向面积重叠度越小,几何完整性越高[9];中心点距离相似度反映两个面状要素的相似程度,中心点距离相似度越大,两个面状要素的相似度越高[10],故使用双向面积重叠度和中心点距离相似度获取面状要素间的距离。
1) 中心点距离法。面状要素几何完整性较高时,中心点的距离可以在一定程度上反映位置精度[10]。独立面状要素直接计算中心点距离,分片的面状要素需先聚合再计算中心点距离。参考数据和测试数据中同一面状要素的中心点(xref, yref)和(xosm, yosm)间的欧氏距离为:
| $ d = \sqrt {{\rm{ (}}{x_{{\rm{ref}}}} - {x_{{\rm{osm}}}}{)^2} + {{({y_{{\rm{ref}}}} - {y_{{\rm{osm}}}})}^2}} $ | (4) |
2) 双向面积重叠度。参考数据和测试数据中同一面状要素的面积分别为Sref和Sosm,求交后得到的重叠部分的面积为Soverlay,其双向面积重叠度为:
| $ {\delta _s} = 1 - \frac{1}{2}({S_{{\rm{overlay}}}}/{S_{{\rm{osm}}}} + {S_{{\rm{overlay}}}}/{S_{{\rm{ref}}}}) $ | (5) |
3) 中心点距离相似度。参考数据和测试数据中同一面状要素任意边节点间距离的最大值为U,中线点距离为d,其计算距离相似度为:
| $ {\delta _l} = 1 - \frac{d}{U} $ | (6) |
本文以2014年生产的清华大学校园附近区域的面状要素的DLG数据为参考数据,以相同区域的2016年5月份OSM面状要素数据作为测试数据分析OSM面状要素的位置精度(图 3)。分析发现,两类数据中的面状要素均以建筑物为主,故本文以建筑物为研究对象分析位置精度。参考数据包含1 035个建筑物,测试数据包含404个建筑物。
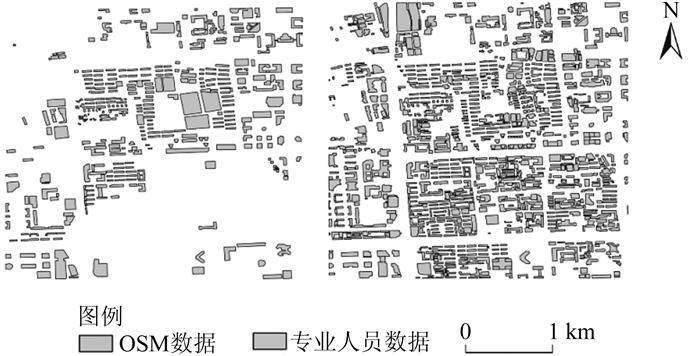 |
| 图 3 实验区域 Fig.3 Test Area |
1) 数据处理。测试数据和参考数据的坐标系分别为WGS-84和CGCS2000。首先将两类数据转换到相同坐标系下,然后根据§1.1中面状要素类型分类方法将建筑物分类。本文重点研究Ⅰ(225个)、Ⅳ(24个)、Ⅴ(23个)类建筑物,OSM总数404个,参考数据总数为1 035个。
2) 完整性检验阈值设定。相似度可以反映测试数据相对于参考数据的完整性,当相似度S为1时,参考数据和测试数据的相似度最高。建筑物的相似度S服从正态分布(图 4),故以±3σ作为完整性检验的阈值(表 1)。
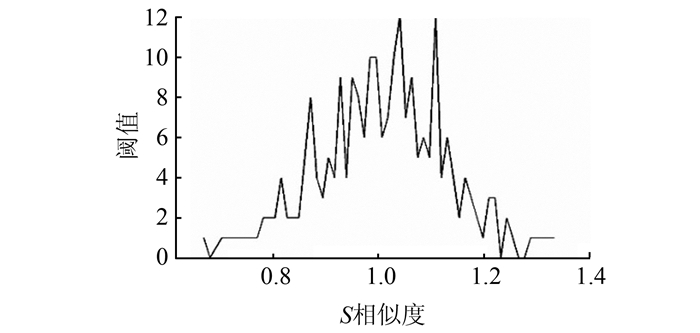 |
| 图 4 S分布图 Fig.4 S Distribution |
| 表 1 完整性检验阈值 Tab.1 Threshold of Integrity |
 |
3) 双向面积重叠度和中心点距离相似度阈值设定。本文已经删除形变较大的建筑物且进行了完整性检验,故双向面积重叠法和中心点距离相似度阈值δs和δl可分别设为0.3和0.8,δs≤0.3且δl≥0.8的建筑物的中心点间距离即为建筑间的距离。
4) 实验结果。主要从完整性和位置精度两个方面来进行检验。
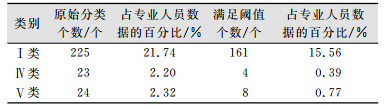
① 完整性检验。总的来说,OSM建筑物的数据完整性和几何形状完整性都较低。OSM建筑物总数仅占官方建筑物总数的39.03%,表明OSM建筑物的数据完整性不高。同时通过完整性检验的OSM建筑物总数仅占官方建筑物总数的16.7%,表明OSM建筑物的几何完整性也不高(表 2)。
| 表 2 建筑物完整性检验结果 Tab.2 Result of Building Integrity Test |
 |
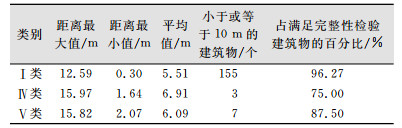
② 位置精度检验。通过中心点距离法计算OSM数据和专业人员数据中同一建筑物中心点间的距离,结果显示中心点间距离在5~10 m之间聚集(图 5),平均值为6±1 m(表 3),3类建筑物中心点间的距离最大值分别为12.59 m、15.97 m、15.84 m。
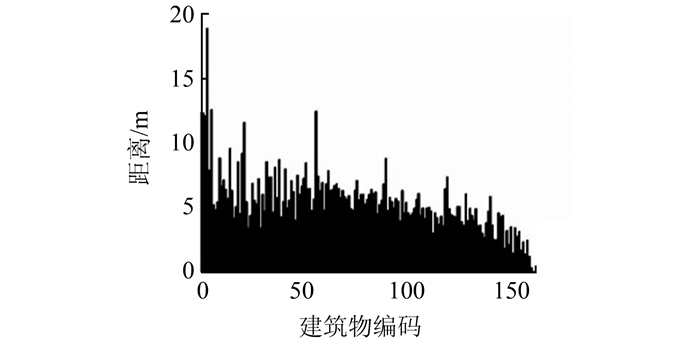 |
| 图 5 建筑物中心点距离分布图 Fig.5 Building Center Points Distance Distribution |
| 表 3 建筑物中心点距离结果 Tab.3 Result of Center Distance Method |
 |
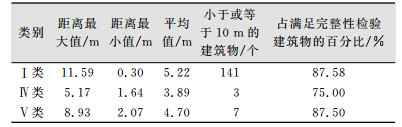
使用双向面积重叠度和中心点距离相似度确定建筑物间的距离。双向面积重叠度和中心点距离相似度结果显示,Ⅰ、Ⅳ、Ⅴ类中建筑物间距离的最大值分别为11.59 m、5.17 m、8.93 m(表 4),相比于建筑物中心点间的距离(表 3)均有下降。3类建筑物中通过双向面积重叠度和中心点距离相似度检验的建筑物总数占通过完整性检验建的筑物总数的百分比分别为88.2%、75%、87.5%(表 5);以民用GPS 10 m的定位精度为位置精度,满足该精度的建筑物总数占通过完整性检验的建筑物总数的百分比分别为87.58%、75%和87.5%(表 4)。以上结果表明,整体上完整性较好的OSM建筑物的位置精度也较高,但局部仍然存在部分建筑物完整性较高但位置精度较低。
| 表 4 建筑物间距离结果 Tab.4 Result of Building Distanc |
 |
| 表 5 建筑物间距离统计 Tab.5 Statistics of Building Distance |
 |
3 结束语
目前,尚未有关于OSM面状要素位置精度检验的方法,面状要素作为OSM地图的重要组成部分,检验其位置精度对OSM地图普及和应用非常重要。本文以OSM地图数据中的面状要素为研究对象,提出了面状要素位置精度分析方法。分析结果显示,OSM中完整性较好的面状要素仅占专业人员数据的16.7%,其中约87.5%的面状要素与专业人员获取的数据中相应的面状要素间距离的平均值为5±1 m,且最大值小于12 m。本文的实验结果为OSM地图数据的研究和应用提供了理论基础,对于OSM面状要素,其数据完整性和几何完整性较差,即使是完整性较好的面状要素,在进行与地理位置相关的活动中,都要有选择的使用。此外,由于专业人员数据获取困难,本文数据样本较小,未来可通过大样本数据进行更全面的研究。
| [1] |
Goodchild M F. Citizens as Sensors:The World of Volunteered Geography[J]. GeoJournal, 2007, 69(4): 211-221. DOI:10.1007/s10708-007-9111-y |
| [2] |
Mordechai H. How Good Is Volunteered Geographical Information[J]. A Comparative Study of OpenStreetMap and Ordnance Survey Datasets Environment and Planning B:Planning and Design, 2010, 93(11A): 3-11. |
| [3] |
Zulfiqar N. A Study of the Quality of OpenStreetMap.org Maps: A Comparison of OSM Data and Ordnance Survey Data[D]. London: University College London, 2008
|
| [4] |
李亚平, 蔡忠亮, 谢彩云, 等. 一种开放式地理空间数据可用性评价方法的研究[J]. 测绘地理信息, 2017, 42(1): 83-87. |
| [5] |
王明, 李清泉, 胡庆武, 等. 面向众源开放街道地图空间数据的质量评价方法[J]. 武汉大学学报·信息科学版, 2013, 38(12): 1 490-1 494. |
| [6] |
赵肄江, 周晓光. 地理信息志愿者信誉度评估的版本相似度模型——以面目标为例[J]. 测绘学报, 2015, 44(5): 578-584. |
| [7] |
Schmitz Z A, Neis S P. New Applications Based on Collaborative Geodata-The Case of Routing[C]. The 28th INCA International Congress on Collaborative Mapping and Space Technology, Gandhinagar, Gujarat, India, 2008
|
| [8] |
Adler B, Alfaro L.A Content-Driven Reputation System for the Wikipedia[C]. The 16th International Conference on World Wide Web, ACM, Alexandria, Virginia, USA, 2007
|
| [9] |
吴建华.矢量空间数据实体匹配方法与应用研究[D].武汉: 武汉大学, 2008
|
| [10] |
邵世维.基于几何特征的多尺度矢量面状实体匹配方法研究与应用[D].武汉: 武汉大学, 2011
|
| [11] |
孟凡相, 程耀东, 王欣. 面状要素化简前后相似度计算方法研究[J]. 测绘科学, 2009(S2): 91-93. |
 2019, Vol. 44
2019, Vol. 44

