| 一种状态区间取值修正的灰色-马尔科夫链预测模型研究 |
现实生活中, 地表建筑物往往会受到各种外力影响, 从而产生变形。沉降预测对变形监测是相当重要的, 可确保建筑物安全, 减少和避免不必要的损失。目前常用的预测方法有: 灰色模型、时间序列模型、人工神经网络等。灰色模型具有算法简单、能够处理残缺信息[1]、所需数据量小等优势, 但后效性较大, 预测值存在沿原趋势的惯性; 时间序列模型精度高, 但是要求序列零均值且足够平稳, 对数据样本量要求较高; 人工神经网络精度较前两者更高, 工程中较为常用, 但是需要考虑到建筑物所处区域的多方面因素, 对建模者专业知识要求高, 算法复杂。黄传胜使用基于时间序列的BP神经网络预测深基坑沉降, 中长期预测精度较佳, 然而这需要找准大量影响因素, 且工程初期数据量无法达到模型要求[2]; 张振勇用灰色模型拟合序列的趋势项, 用时序模型拟合序列的波动项, 组合模型在仅具有少量数据的条件下取得了较好的沉降预测效果[3]。马尔科夫链(Markov Chain)仅关注现在状态的影响, 具有无后效性, 常与时间序列、灰色模型组合使用。本文提出了一种状态区间取值修正方法, 消除了一部分状态区间划分误差, 提高了马尔科夫链的可靠性。与灰色模型、残差修正灰色模型、修正前的组合模型对比的结果表明, 该方法具有可行性, 精度有较大提升。
1 改进的灰色-马尔科夫链组合模型的建立 1.1 灰色模型传统GM(1, 1)总体思路是根据已知实测数据构建原始序列、累加序列和紧邻均值序列, 解求模型参数, 累减后得到预测值序列。过程如下:
1) 将不等时距的观测数据通过线性插值[4]得到等时距数据序列X(0)。
2) 由原始序列X(0)一次累加得到1-AGO序列X(1)和紧邻均值序列Z(1)。
3) 最小二乘估计灰参数a、u[5]。
4) 计算预测值累加序列
5) 累减还原预测值序列
| $ {\hat{X}}^{\left(0\right)}=\left\{{x}^{\left(0\right)}\left(1\right), {\hat{x}}^{\left(0\right)}\left(2\right), {\hat{x}}^{\left(0\right)}\left(3\right), \dots , {\hat{x}}^{\left(0\right)}\left(n\right)\right\} $ | (1) |
式中,
当用于灰色模型建模的数据较多时, 一般采用残差修正的方法, 由较新数据的残差建立灰色模型, 将残差预测值用于模型修正, 改善模型精度。具体步骤如下:
1) 由残差构建原始序列V(0):
| $ {V}^{\left(0\right)}={\hat{X}}^{\left(0\right)}-{X}^{\left(0\right)} $ | (2) |
一般仅取接近预测时刻的[n/2]期数据。
2) 按照§1.1的建模步骤, 得到残差预测值序列
3) 计算残差修正后的模型预测值序列
马尔科夫链具有无后效性, 即已知过去t1-tn-1和现在tn时刻状态的条件下, 将来tn+1时刻状态仅依赖于现在tn时刻状态, 而与过去t1-tn-1时刻状态无关[7], 具体实现过程如下:
1) 由§1.2得到模型预测值曲线γ'(k), 在曲线的上部和下部, 依据已知数据的相对误差绘制折线图, 划分状态区间(图 1), 由此构造出条形带状区域, 每一区域代表一个状态[8]。
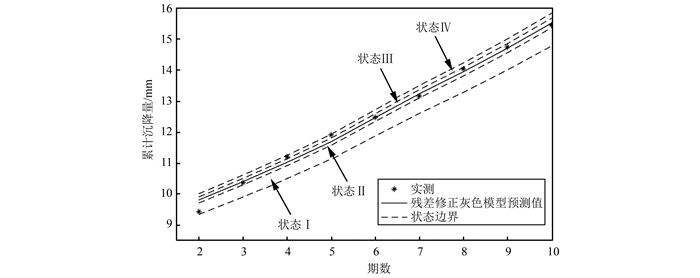 |
| 图 1 预测值曲线与状态区间划分 Fig.1 Prediction Value Curve and State Interval Division |
2) 计算转移概率矩阵: 一步转移概率矩阵
| $ {\mathit{\boldsymbol{P}}}^{\left(1\right)}=\left[ {\begin{array}{*{20}{c}} {{p_{11}}} & \cdots & {{p_{1n}}}\\ \vdots & {} & \vdots \\ {{p_{n1}}} & \cdots & {{p_{nn}}} \end{array}} \right] $ | (3) |
n步转移概率矩阵可用来表达任意时刻到n步后时刻状态的转移概率[13]。
| $ {\mathit{\boldsymbol{P}}}^{\left(n\right)}={\mathit{\boldsymbol{P}}}^{{\left(1\right)}^{n}} $ | (4) |
3) 根据状态区间为组合模型预测值
| $ {\hat{\gamma }}^{'}\left(k\right)=\frac{{\mathrm{\gamma }}^{'}\left(k\right)}{1+\frac{{f}_{1}M+{f}_{2}N}{{f}_{1}+{f}_{2}}} $ | (5) |
式中, M, N取相对误差作为区间左右端点,
4) 状态区间修正: 考虑到测量数据误差的不确定性以及系统中各种影响因素的作用, 各个状态区间中的数据(本文取相对误差)往往不会均匀地分布, 甚至会出现聚集在某一区间端点附近的情况。因此, 本文提出状态区间取值修正改进的方法, 具体如下: 计算转移概率矩阵的同时, 记录数据在状态区间中的位置; 根据数据位置确定区间两端的权值:
对于Qi状态区间[Mi, Ni]中的数据平均位置Li(距左端点的距离), 有:
| $ {L}_{i}=\frac{1}{{n}_{i}}\sum\limits _{j=1}^{{n}_{i}}({x}_{j}-{M}_{i}) $ | (6) |
左、右两端权值f1、f2:
| $ {f}_{1}=\frac{{L}_{i}}{{N}_{i}-{M}_{i}} $ | (7) |
| $ {f}_{2}=1-{f}_{1} $ | (8) |
式中, ni为被划分为Qi状态的数据个数, xj为Qi状态中的数据, Mi、Ni为Qi状态区间左、右端点。
1.4 改进的灰色-马尔科夫链组合模型的建立流程依据上述原理, 基于状态区间取值修正的灰色-马尔科夫链组合模型构建流程如图 2所示。
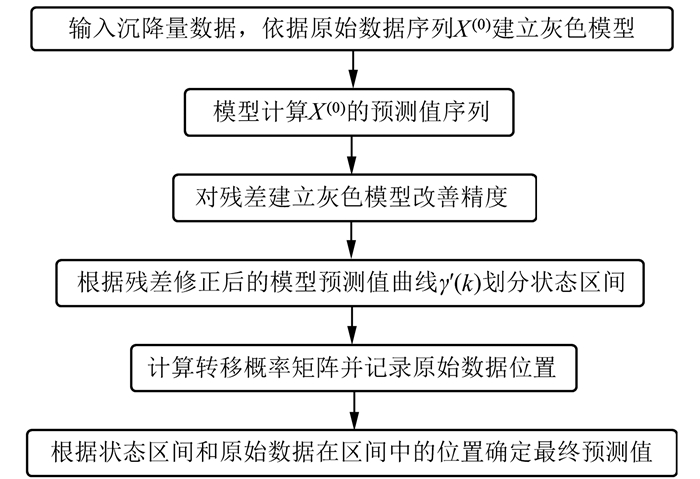 |
| 图 2 模型构建流程 Fig.2 Process of Building Model |
2 工程应用与效果分析
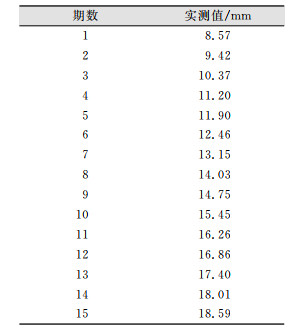
本文选取了某建筑物连续15期实测累计沉降量数据(见表 1), 用1~10期进行建模预测11~15期的累计沉降量, 并与实测进行比较。
| 表 1 实测累计沉降量数据 Tab.1 Measured Cumulative Settlement Data |
 |
2.1 状态区间取值修正的灰色-马尔科夫链组合预测模型的构建
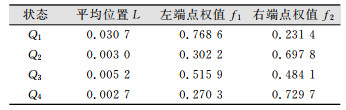
按照§1.4的流程, 取1~10期数据建模。其中, 根据相对误差划分状态区间如下: Q1∈[0.010, 0.050], Q2∈[0, 0.010], Q3∈[-0.010, 0], Q4∈[-0.020, -0.010]。1~10期的相对误差状态分布情况如表 2所示, 平均位置及权值如表 3所示。
| 表 2 相对误差状态分布表 Tab.2 Distribution of Relative Error State |
 |
| 表 3 平均位置及权值 Tab.3 Average Position and Weight |
 |
2.2 结果分析与比较
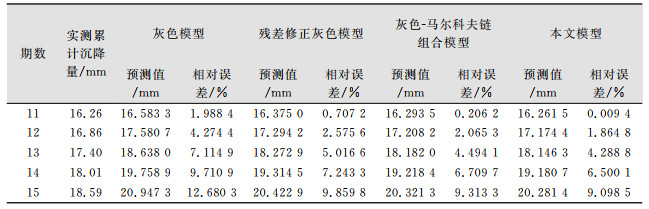
为了说明本文模型的有效性, 选取了灰色模型、残差修正灰色模型、灰色-马尔科夫链组合模型与其比较, 经过计算, 各模型11~15期预测值结果如表 4和图 3所示。
| 表 4 各模型对比 Tab.4 Comparison of Each Model Prediction |
 |
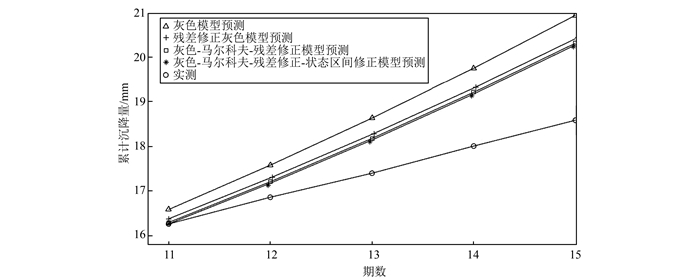 |
| 图 3 各模型预测值对比 Fig.3 Comparison of Each Model Prediction Results |
结合图 3和表 4可知, 本文模型预测曲线最接近实测, 相对误差比其他三者小, 精度最高。进一步分析可以看出, 马尔科夫链对灰色模型有较好的修正效果, 而状态区间修正则是在马尔科夫链的基础上作进一步修正, 对精度有一定的改善。
3 结束语为减小状态区间划分和以往传统灰色-马尔科夫链取值的误差, 本文提出了一种状态区间取值修正方法, 并依此构建了基于状态区间取值修正的灰色_马尔科夫链组合模型。建筑物沉降量实际数据和不同模型预测的对比结果显示, 修正后的组合模型精度更高, 说明了该方法的实用性。
| [1] |
李志伟, 李克昭, 赵磊杰, 等. 多变量灰色马尔科夫模型在建筑物沉降预测中的应用[J]. 测绘地理信息, 2018, 43(3): 36-40. |
| [2] |
袁红磊, 花向红, 龚国栋, 等. 小波与时间序列组合模型分析和预测建筑物沉降变形[J]. 测绘地理信息, 2018, 43(2): 73-75. |
| [3] |
马成龙, 刘帅, 苗昌奇, 等. 基于灰色-时序组合模型的建筑物沉降预测方法[J]. 测绘与空间地理信息, 2018, 41(11): 198-200. DOI:10.3969/j.issn.1672-5867.2018.11.058 |
| [4] |
成枢, 冯子帆, 郭祥琳, 等. 不同灰色GM(1, 1)模型在地铁沉降预测中的效果分析[J]. 测绘地理信息, 2019, 44(1): 14-17. |
| [5] |
黄传胜. 地铁深基坑开挖变形预测方法及工程应用研究[D]. 长沙: 中南大学, 2011
|
| [6] |
张振勇. 灰色-时序组合模型在建筑物变形预测中的应用研究[D]. 天津: 天津大学, 2007
|
| [7] |
黎洋, 花向红, 姚周祥, 等. 傅里叶级数修正的动态GM(1, 1)模型在沉降预测中的应用[J]. 测绘地理信息, 2017, 42(1): 30-33. |
| [8] |
易梅, 高雅萍, 郭瑞雪, 等. 动态残差修正的新陈代谢灰色模型在沉降预测中的应用[J]. 工程勘察, 2018(4): 44-48. |
| [9] |
田振凯, 李瑞海, 许彦国. 动态灰色-时序模型在建筑物沉降预测中的应用[J]. 测绘与空间地理信息, 2018, 41(10): 228-230. DOI:10.3969/j.issn.1672-5867.2018.10.070 |
| [10] |
黄声享. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2010.
|
| [11] |
田铮, 秦超英. 随机过程与应用[M]. 北京: 科学出版社, 2007.
|
| [12] |
潘国荣, 乔立洋. 非等间距改进灰色模型在基坑变形预测中的应用[J]. 测绘地理信息, 2019, 44(1): 9-13. |
| [13] |
高蔚. 基于Markov理论的改进灰色GM(1, 1)预测模型研究[J]. 计算机工程与科学, 2011(2): 159-163. |
 2021, Vol. 46
2021, Vol. 46

