| 越南水电站大坝变形分析研究 |
2. THUY LOI University, 175 Tay Son street, Dong Da District, Hanoi, Vietnam;
3. LE QUY DON Technical University, 100 Hoang Quoc Viet street, Cau Giay District, Hanoi, Vietnam
2. THUY LOI University, 175 Tay Son street, Dong Da District, Hanoi, Vietnam;
3. LE QUY DON Technical University, 100 Hoang Quoc Viet street, Cau Giay District, Hanoi, Vietnam
越南和平水电站于1982年开工,1993年完工,该工程位于越南北部红河右岸最大的支流沱江上,河槽宽约222~280 m,两岸谷坡大于30°。和平水电站的坝体是土石坝类型,最大坝高128 m,坝址基岩由火成岩组成,包括辉绿岩、玄武斑岩、角砾岩和细碧岩,基岩裂隙十分发育。坝址控制流域面积52 600 km2,多年平均径流量1 800亿m3,最大实测流量21 000 m3/s。根据降水特点,可划分出两个明显不同的季节:6~10月为丰水期,11月~次年5月为枯水期。水库正常蓄水位117 m,最高水位120 m,死水位90 m,有效库容56.5亿m3。水库总库容94.5亿m3,水电站装机容量为192万kW,年平均发电量82亿kWh。工程主要用于防洪和发电,和平水电站投运后,使越南电力增加2倍,改善了红河下游地区防洪条件,提高了枯水航深,库区形成200多km的深水航道。
和平水电站变形监测数据采用视准线法获得了将近12 a的水平横向位移数据。近几十年来,时间序列法和BP(back propagation)神经网络法是大坝水平位移预测的主要方法。由于大坝变形具有季节性,在具有充足的历史数据条件下,采用时间序列法,通过分析大坝的全部观测数据,能有效地分析和描述大坝的变形特性。BP神经网络是一种多层前馈型神经网络,是目前应用最为广泛和取得成果最为突出的神经网络之一,在变形预测方面有着很大的优势。本文采用季节性时间序列法(seasonal auto-regressive integrated moving average,SARIMA)模型和BP神经网络模型对获得的历史变形数据进行分析预测,通过与相应的实际值进行对比,结果表明这两种方法都能合理、准确地描述和平水电站的变形趋势。
1 视准线法视准线法属于基准线法,其原理是通过建筑物轴线或平行于建筑物轴线的固定铅直平面为基准面来测定建筑物的水平位移,经常用于大坝水平位移观测[1]。在大坝轴线两端的固定点间安置经纬仪和固定觇牌,将二者间的视线作为基准线,在经纬仪和固定觇牌之间安置观测点,定期测量观测点到基准线间的距离,可求定观测点水平位移量。
如图 1所示,将经纬仪安置在基准线的一端A点,将固定觇牌安装在基准线另一端B点;将经纬仪瞄准B点觇牌,使视线固定形成基准线;在观测点C安置活动觇牌,观测时,移动活动觇牌,使照准标志与经纬仪的十字丝重合,记录分划尺和游标尺上的读数;移动活动觇牌从相反方向重新对准并读数。
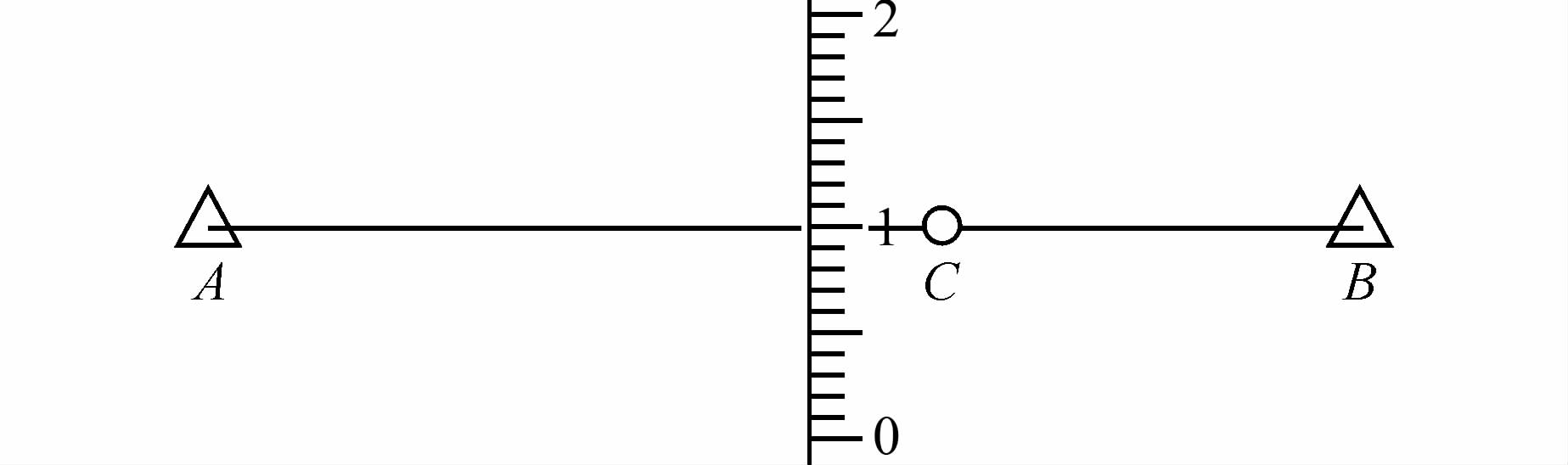 |
| 图 1 视准线观测法 Figure 1 Alignment Monitoring Method |
2 数据分析模型 2.1 SARIMA模型
平稳时间序列满足期望为零,均值在所有时间上均为常数,且任意两个时刻的相关函数与时间t无关,仅与两个时刻的时间差相关[2],其中滑动平均过程可描述为: 当有限个系数θ不为零时,就得到滑动平均过程,模型如下:
| ${{Y}_{t}}={{e}_{t}}-{{\theta }_{1}}{{e}_{t-1}}-{{\theta }_{2}}{{e}_{t-2}}-...-{{\theta }_{q}}{{e}_{t-q}}$ | (1) |
上式称为q阶滑动平均过程,记为MA(q)。
自回归过程可描述为用自身做回归变量,p阶自回归过程满足方程:
| ${{Y}_{t}}={{\varphi }_{1}}{{Y}_{t-1}}+{{\varphi }_{2}}{{Y}_{t-2}}+...+{{\varphi }_{q}}{{Y}_{t-q}}+{{e}_{t}}$ | (2) |
上式记为AR(p),序列Yt的当期值是自身最近p滞后项和新信息项et的组合,其中et包含了序列在t期无法用过去值来解释的所有新信息。
引入后移算子B,式(1) 、式(2) 可转化为:
| ${{Y}_{t}}=\theta \left( B \right){{e}_{t}}$ | (3) |
| $\varphi \left( B \right){{Y}_{t}}={{e}_{t}}$ | (4) |
式中, BjYt=Yt-j;θB=1-θ1B-θ2B2-…-θqBq;φB=1-φ1B-φ2B2-…-φpBp。
如果假定序列中部分是自回归,部分是滑动平均,就可以得到一个相当于普遍的时间序列模型:
| ${{Y}_{t}}={{\varphi }_{1}}{{Y}_{t-1}}+{{\varphi }_{2}}{{Y}_{t-2}}+...+{{\varphi }_{q}}{{Y}_{t-q}}+{{e}_{t}}-{{\theta }_{1}}{{e}_{t-1}}-{{\theta }_{2}}{{e}_{t-2}}-...-{{\theta }_{q}}{{e}_{t-q}}$ | (5) |
上式称为Yt自回归滑动平均混合过程,阶数分别为p和q,记为ARMA(p,q)。或
| $\varphi \left( B \right){{Y}_{t}}=\theta \left( B \right){{e}_{t}}$ | (6) |
若时间序列因为具有某种趋势性而不满足平稳性条件,经过d阶差分后序列平稳,记新序列为: Wt=▽dYt,其中d为差分次数。
如果一个时间序列Yt的d次差分Wt=▽dYt是一个平稳的ARMA过程,则称Yt为自回归滑动平均求和模型,记为ARIMA(p,d,q)。或
| $\varphi \left( B \right){{\nabla }^{d}}{{Y}_{t}}=\theta \left( B \right){{e}_{t}}$ | (7) |
有些序列进行差分后仍不能平稳,这是由于序列的季节性变化引起的周期性变化,这种季节性包括周度、月度、季度、年度等变化[3],这种模型就是SARIMA模型,即
| ${{\varphi }_{p}}\left( B \right){{\Phi }_{P}}\left( {{B}^{S}} \right){{\left( 1-B \right)}^{d}}{{\left( 1-{{B}^{S}} \right)}^{D}}{{Y}_{t}}={{\theta }_{q}}\left( B \right){{\Psi }_{Q}}\left( {{B}^{S}} \right){{e}_{t}}$ | (8) |
式中,φpB为自回归特征多项式;ΦPBS为季节自回归特征多项式;θqB为滑动平均特征多项式;ΨQBS为季节滑动平均特征多项式;D、d分别表示非季节性和季节性差分的次数;S为季节周期长度。
SARIMA建模过程如下:
1) 数据平稳化处理。通过差分或其他变换,将非平稳时间序列转换为平稳时间序列,并确定差分阶数即参数d的数值,使时间序列满足平稳性。
2) 模型识别。主要是确定参数p、d、q和P、D、Q以及S的值,根据时间序列模型的识别规则,建立相应的模型并确定其参数值。一般根据自相关和偏相关图初步判断时间序列的阶数,然后采用由低阶向高阶逐次探索的方法确定模型的类型和阶数。
3) 参数估计和模型诊断。确定了p、d、q、P、Q、D以及S的值,即确定了模型的具体类型。进而估计出各个参数的具体数值,对估计值进行检验,判断是否符合检验标准条件。
4) 模型预测。利用已经确定了具体参数值的最优模型对序列的未来取值或走势进行预测。
2.2 BP神经网络模型人工神经元可以将已知信号进行加权求和处理[4],其常用表达式为:
| $y=\sum\limits_{i=1}^{n}{{{w}_{i}}{{x}_{i}}+b}$ | (9) |
其中,xii=1,2,…,n为网络的输入值;wii=1,2,…,n表示网络的权重;b为阈值;y为网络的输出值。
BP神经网络意思是前馈式误差反传神经网络,一般由输入层、隐含层和输出层构成[5],每层含若干个神经元,各层之间神经元采用全互联的连接方式通过权重连接,每层内的神经元之间没有连接,通常BP神经网络是含有一个隐含层的三层结构网络,如图 2所示。
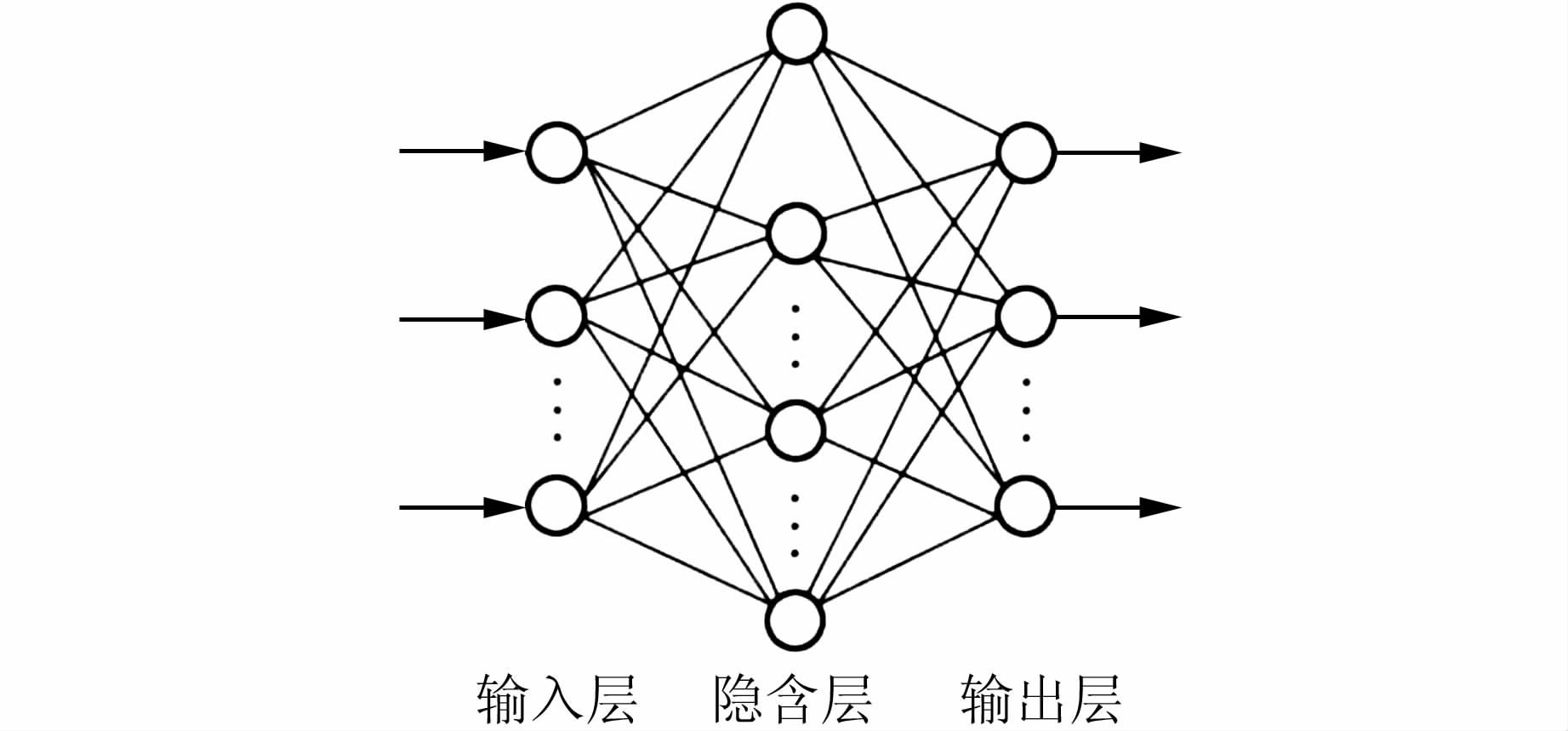 |
| 图 2 BP神经网络结构 Figure 2 Structure of BP Neural Network |
假设某BP神经网络输入神经元个数为n,输出神经元 个数为m,隐含层神经元个数为p,则隐含层神经元的输出为:
| $x_{i}^{j}=\sigma \left( \sum\limits_{i=1}^{n}{{{w}_{ij}}{{x}_{i}}+{{b}_{j}}} \right),j=1,2,...,p$ | (10) |
输出层神经元输出为:
| ${{y}_{k}}=\sum\limits_{j=1}^{p}{{{w}_{ik}}{{x}_{j}}+{{b}_{k}},k=1,2,...,m}$ | (11) |
激活函数常采用Sigmoid函数:
| $f(x)={{(1+{{e}^{-ax}})}^{-1}}$ | (12) |
式中,a为常数。
BP神经网络建模过程为:
1) 根据数据选定BP神经网络的结构,选择隐层和输出层神经元激活函数,确定合适的网络训练方法;
2) 对输入数据和输出数据进行归一化处理;
3) 用函数newff()构造神经网络;
4) 在对神经网络训练之前,首先设定相关参数,如最大训练次数、训练要求精度、学习率等;
5) 对BP神经网络进行训练;
6) 重复训练,直到满足要求为止;
7) 保存训练好的神经网络,并用训练好的神经网络进行预测;
8) 将预测值和实际输出值进行对比,分析模型的稳定性。
3 变形分析及预测 3.1 时间序列法在和平水电站大坝设置多个观测点,以其中的PVM2点的水平横向位移数据进行分析。历史数据为近12 a的观测值共137期,如图 3所示。
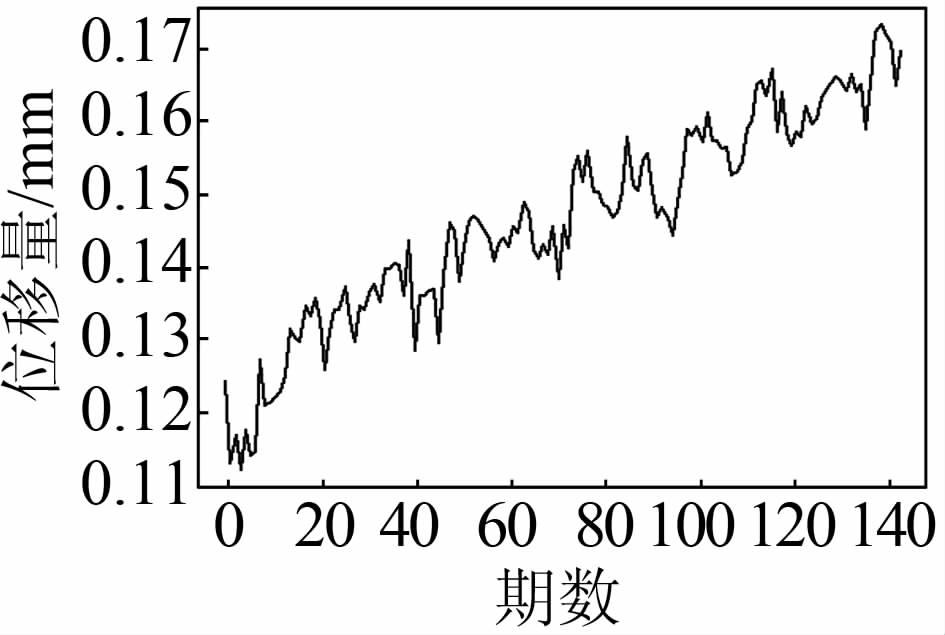 |
| 图 3 PVM2水平横向位移 Figure 3 Transverse Displacement of PVM2 Point |
由图 3可以看出,大坝位移具有明显的非平稳性,位移量随着时间推移有着增长的趋势,考虑到大坝位移受水位和温度的周期影响,可以判断该大坝的位移的季节性周期为S=12。对该序列作1阶差分和1阶季节性差分得到的序列如图 4所示。
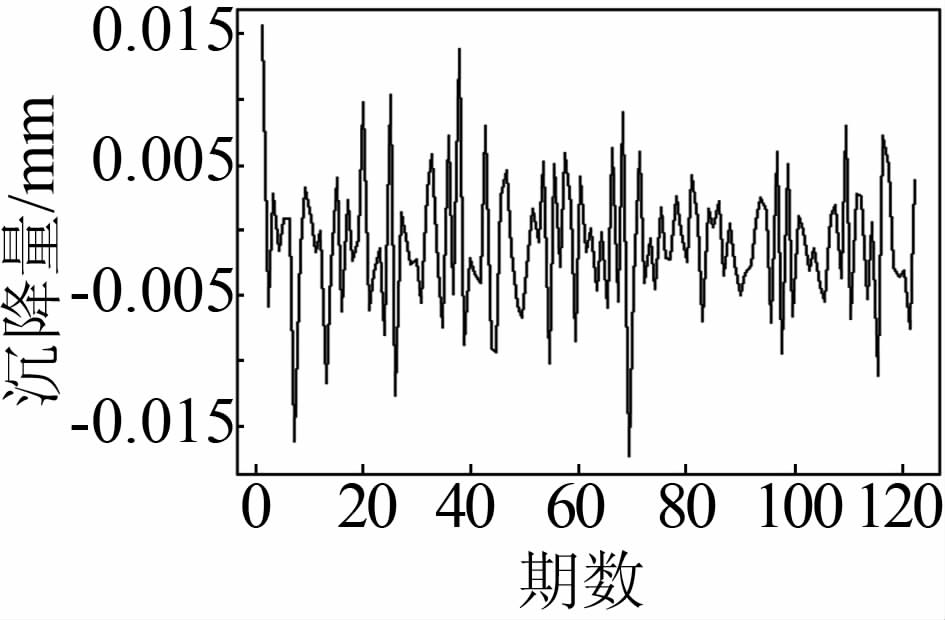 |
| 图 4 差分PVM2水平横向位移 Figure 4 Differential Displacement of PVM2 Point |
对差分后的序列进行ADF(augmented Dickey-Fuller)单位根检验[6],如表 1所示。
| 表 1 差分后的ADF检验 Table 1 After ADF Test |
 |
由表 1可以看出,检验统计量比各显著性水平临界值都小,所以差分后的序列具有平稳性。此时可以判定参数d=1,D=1。观察差分序列的自相关函数ACF(autocorrelation function)图和偏自相关函数PACF(partial autocorrelation function)图,如图 5所示。
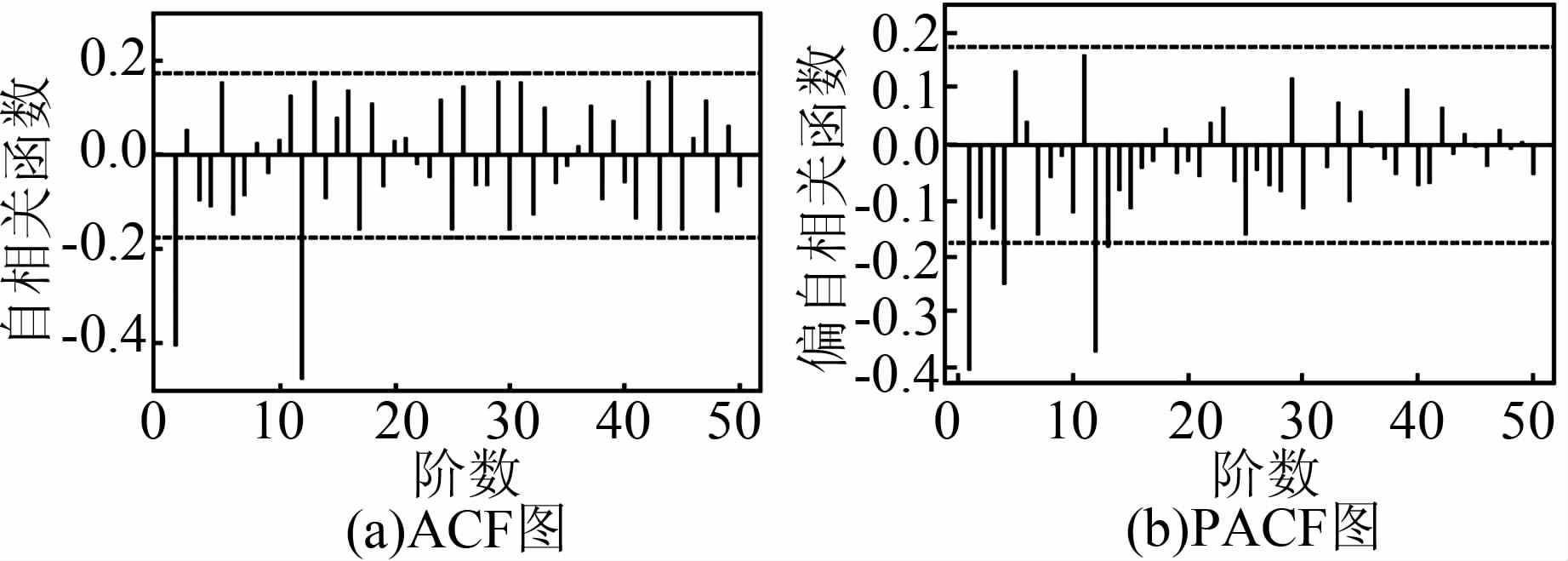 |
| 图 5 差分序列的ACF图和PACF图 Figure 5 ACF and PACF Charts of Difference Time Series |
由图 5可以看出,差分序列的自相关系数是拖尾的,在1阶和12阶显著大于置信区间的范围,可以判断q=1,Q=1;而从PACF图可以看出,在1阶、4阶和12阶系数超出置信区间,初步认定p=1,P=1。为了确定最佳拟合模型,采用AIC(Akaike information criterion)标准[7],选择AIC值最小的模型作为最佳模型。经选择,适合的模型有7个,见表 2。最终确定最优模型为SARIMA(1,1,1) (1,1,1) 12。在参数估计后进行残差白噪声检验,结果显示残差具有白噪声特性。
| 表 2 模型的AIC值 Table 2 AIC Values of SARIMA Model |
 |
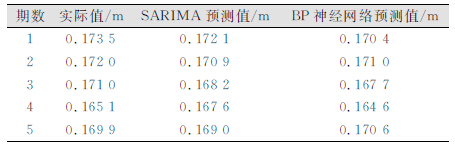
采用该模型进行未来5期的预测,预测结果与实际值比较,结果见表 3。
| 表 3 预测值与实际值对比 Table 3 Comparison of Forecast and True Values |
 |
3.2 BP神经网络法
BP神经网络法采用滚动式的预测方法来预测其误差。以1至12期预测误差为网络输入,第13期为网络输出;2至13期预测误差为网络输入,第14期为网络输出;以此类推到125~136期为网络输入,137期为网络输出,组成样本进行网络训练。经过反复实验,选择隐含层神经元个数为10。
权值训练算法采用L-M优化算法[8],训练次数设为500,训练精度为10-5,学习速率为0.01。网络经过124次训练到达最小误差。对该序列未来1期进行预测,得到的预测值作为新一期样本,结合最后11期作为输入值再进行预测,一共预测未来5期,并与实际值比较,其结果见表 3。
3.3 结果精度分析为对比这两种模型的预测精度,采用误差平方和SSE(sum square error)、均方误差MSE(mean square error)、平均绝对误差MAE(mean absolute error) 这几项误差指标来度量。其计算公式分别为:
| $\begin{align} & SSE=\sum\limits_{t=1}^{N}{{{({{x}_{t}}-{{\overset{\wedge }{\mathop{x}}\,}_{t}})}^{2}}} \\ & MSE=\frac{1}{N}\sqrt{\sum\limits_{t=1}^{N}{{{({{x}_{t}}-{{\overset{\wedge }{\mathop{x}}\,}_{t}})}^{2}}}} \\ & MAE=\frac{1}{N}\sum\limits_{t=1}^{N}{\left| {{x}_{t}}-{{\overset{\wedge }{\mathop{x}}\,}_{t}} \right|} \\ \end{align}$ |
| 表 4 两种模型的预测精度 Table 4 Forecast Accuracy of Two Models |
 |
部分实际值与预测值的趋势在图 6中展示。
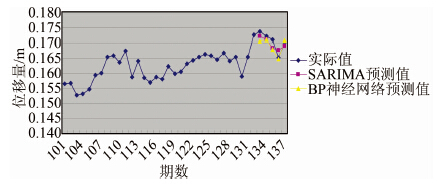 |
| 图 6 实际值与预测值趋势 Figure 6 Trends of True Value and Forecast Value |
由表 4和图 6可知,两种模型预测精度相差不大,且基本能反映大坝的变形趋势,都表现了周期性的特点,说明大坝的变形具有季节性。
4 结束语本文采用了视准线法进行大坝位移量数据的采集,该方法在现阶段依然具有重要的应用价值,能准确高效地获得大坝位移量。
根据观测点PVM2的近12 a变形数据进行分析和预测,由预测值与实测值的拟合情况和各模型残差指标来看,说明运用这两种模型建模能较好地反映大坝位移观测点测值的变化规律和变化趋势,大坝位移变形主要受周期性温度和水位变化所致,总体有定向位移的趋势。可以通过历史的观测值序列建立两种模型来分析预报未来短时期内的变化量,将未来实际值和预报值结合起来进一步校核模型,用来反馈模型的适用性;并在更新数据的前提下建立新的最优模型,使模型向前延续。
分析研究表明,这两种模型在短期预测应用中具有较好的精度,对于长期预测不一定有效,实际应用中需进一步检验。
| [1] |
杜治国. 大坝水平位移视准线观测方法及精度分析[J].
大坝与安全,2006,(5) : 25–29.
Du Zhiguo. Accuracy Analysis on the Methods of Alignment of Observing Dam Horizontal Displacement[J]. Dan and Safety,2006,(5) : 25–29. |
| [2] | Cryer J D, Chan K S. Time Series Analysis with Application in R[M]. Beijing: China Machine Press, 2011 . |
| [3] |
董骞.基于SARIMA模型及状态空间模型对我国出口的预测[D].兰州:兰州大学,2014 Dong Qian. The Prediction of Chinese Export Based on SARIMA Models and State Space Models [D].Lanzhou: Lanzhou University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10730-1014301853.htm |
| [4] |
雷可为, 陈瑛. 基于BP神经网络和ARIMA组合模型的中国入境游客量预测[J].
旅游学刊,2007,(4) : 20–25.
Lei Kewei, Chen Ying. Forecast of Inbound Tourists in China Based on the Combination of BP Neural Network and ARIMA Model[J]. Tourism Tribune,2007,(4) : 20–25. |
| [5] |
李友坤.BP神经网络的研究分析及改进应用[D].淮南:安徽理工大学,2012 Li Youkun. Analysis and Improvement Applications of BP Neural Network[D].Huainan: Anhui University of Science & Technology,2012 http://www.oalib.com/references/18699751 |
| [6] |
夏天. SARIMA模型的建模及其信贷预测分析[J].
华侨大学学报,2006,27(3) : 329–332.
Xia Tian. Analysis of SARIMA Modeling and Its Prediction of Credit[J]. Journal of Huaqiao University,2006,27(3) : 329–332. |
| [7] |
孙湘海, 刘潭秋. 基于SARIMA模型的城市道路短期交通流预测研究[J].
公共交通科技,2008,25(1) : 129–133.
Sun Xianghai, Liu Tanqiu. Study on Urban Road Short-term Traffic Flow Forecasting Based on SARIMA Time Series Model[J]. Journal of Highway and Transportation Research and Development,2008,25(1) : 129–133. |
| [8] |
李炯城, 黄汉雄. 神经网络中LMBP算法收敛速度改进的研究[J].
计算机工程与应用,2006,(16) : 46–50.
Li Jiongcheng, Huang Hanxiong. Research on Improvement of Convergence Speed of LMBP Algorithm in Neural Network[J]. Computer Engineering and Applications,2006,(16) : 46–50. |
 2016, Vol. 41
2016, Vol. 41


