| 时间序列分析在变形数据分析中的应用 |
2. 四川电力设计咨询有限责任公司,四川 成都 610041
2. Sichuan Electric Design and Consulting Company Ltd, Chengdu 610041, China
从工程建(构)筑物的施工开始到竣工,以及建成后的整个运营阶段都要连续地进行变形监测。通过对变形监测数据的科学分析处理,发现变形的原因及其特征规律,进而及时作出科学的预测预报,减少变形对人身安全以及国民经济造成的损失。变形监测数据的分析方法很多,如回归分析、时间序列分析、灰色系统理论、BP神经网络法,小波分析等等[1]。时间序列分析是研究事物发展变化规律的一种定量分析方法,它隶属于统计学但又不同于其他统计方法。时间序列分析的基本思路是通过曲线拟合和参数估计(如最小二乘估计)来建立数学模型,通过研究模型的内部结构及规律,可以正确地分析和预测数据的发展趋势[2]。
本文运用时间序列分析方法对变形监测动态数据进行分析处理,构建了监测数据的时间序列模型,通过对该模型的研究分析、预测,验证其预测的准确率,证明该方法实用性较强,可以及时对建筑物变形做出预警,避免或减少灾害的发生[3]。
1 时间序列分析模型 1.1 时间序列分析的模型结构对于平稳、正态、零均值的时序{xt},若xt的取值不仅与其前n步的各个观测值xt-1, xt-2, …,xt-n有关,而且还与前m步的干扰et-1, et-2, …,et-m有关(m, n=1, 2, 3,…),那么这类系统称为自回归移动平均系统,简记为ARMA (auto-regressive and moving average)系统。
| $ \left\{ \begin{array}{l} {x_t} = {j_0} + {j_1}{x_{t-1}} + ... + {j_p}{x_{t-p}} + {e_t}-{q_1}{e_{t - 1}} - ... - \\ \;\;\;{q_q}{e_{t - q}}, {j_p} \ne 0, {q_q} \ne 0\\ E({e_t}) = 0, Var({e_t}) = {s^2}_e, E({e_t}{e_s}) = 0, s \ne t\\ E({x_s}{e_t}) = 0, \forall s < t \end{array} \right. $ | (1) |
具有如下结构的模型称为ARMA (p, q)模型:et为白噪声序列,特别是j0=0时,称为中心化ARMA (p, q)模型,引进延迟算子,中心化ARMA (p, q)模型又可以简记为:
| $ F\left( B \right){X_t} = Q\left( B \right){e_t} $ | (2) |
式中,F(B)=1-j1B-j2B2-…-jPBp, 为p阶自回归系数多项式;Q(B)=1-q1B-q2B2-…-qqBq,为q阶滑动平均系数多项式。
当式(1)中的q=0时,模型即为p阶自回归模型,简记为AR (p)。满足如下条件:
| $ \left\{ \begin{array}{l} {x_t} = {j_0} + {j_1}{x_{t-1}} + ... + {j_p}{x_{t-p}} + {e_t}, {j_p} \ne 0\\ E({e_t}) = 0, Var({e_t}) = {s^2}_e, E({e_t}{e_s}) = 0, s \ne t\\ E({x_s}{e_t}) = 0, s < t \end{array} \right. $ | (3) |
同理,当式(1)中的p=0时,模型称为q阶滑动平均模型,简记为MA (q)。
当测量数据的时间序列是非平稳的,需要进行d阶差分使其平稳化,由此建立的模型为ARMA (p, d, q)模型,在序列的线性趋势非常明显的情况下,一般进行一阶差分就可以实现序列平稳化;而在时间序列表现出“略陡”或线性趋势不明显的情况时,通常需要通过低阶(二阶或三阶)差分才能提取出曲线趋势的影响[4]。ARMA (p, d, q)模型结构为:
| $ \left\{ \begin{array}{l} F(B){\nabla ^d}{x_t} = Q(B){e_t}\\ E({e_t}) = 0, {\rm{Var}}({e_t}) = {s^2}_e, E({e_t}{e_s}) = 0, s \ne t\\ E({x_s}{e_t}) = 0, s < t \end{array} \right. $ | (4) |
相对于d阶的齐次非平稳序列{Xt},{▽dxt}是平稳的,可建立相对应的ARMA模型。
1.2 时间序列分析模型的时域特性时间序列模型是根据平稳时间序列分析建立的随机差分模型,既揭示了动态数据的统计特性, 又揭示了产生此动态数据的系统的动态特性[5]。这些特性均可在时域和频域中得到体现,并且形成了时间序列模型的基本特性。因此本文将重点讨论ARMA模型的最主要的时域特性,如Green函数、自相关函数(auto-correlation function, ACF)、偏自相关函数(partial ACF, PACF)等。
1) Green函数
当可以用一个无关的平稳时间序列{at}的过去值和现在值的线性组合去表示一个相关的平稳时间序列{xt}时,其“权”定义为Green函数,即
| $ {x_t} = \sum\limits_{j = 0}^\infty {{G_j}{a_{t-j}}} $ | (5) |
式中,Gj称为Green函数,G0=1;{at}是彼此无关的白噪声。
ARMA模型的极重要的特性之一就是Green函数,它也是描述模型所对应的等价系统的最主要的动态特性。Green函数是系统的单位脉冲响应函数, 也是Wold正交分解的坐标[6]。
2) 自相关函数与偏自相关函数
对于平稳时间序列{xt},自相关函数表达了xt与xt-k之间的线性依赖关系。
| $ {r_k} = \frac{{{\mathop{\rm cov}} ({x_t}, {x_{t-k}})}}{{\sqrt {{\rm{Var}}({x_t})} \sqrt {{\rm{Var}}({x_{t-k}})} }} = \frac{{{g_k}}}{{{g_0}}} $ | (6) |
rk为平稳、正态的随机过程{xt}的自相关函数[7]。
偏自相关函数的定义为:已知平稳时间序列{xt},如果有一组系数jk1, jk2, …,jkk可以将xt表示为xt-i的线性组合,即
| $ {x_t} = \sum\limits_{i = 1}^k {{j_{ki}}{x_{t-i}}} $ | (7) |
它的误差方差为:
| $ J = E\left[{{{({x_t}-\sum\limits_{i = 1}^k {{j_{ki}}{x_{t-i}}} )}^2}} \right] $ | (8) |
当J非常小时,定义这组系数中的jkk为偏自相关函数,通过解算Yule-Walker方程可求得jkk[8]。
3) 逆函数
当-个相关的平稳时间序列{xt}的现在值和过去值的线性组合可以表示一个无关的平稳时间序列{at}时,其负“权”定义为逆函数[9],即
| $ {a_t} = \sum\limits_{j = o}^\infty {(-{I_j})} {x_{t-j}} $ | (9) |
式中,Ij称为逆函数,-Ij=1。逆函数的性质决定了时间序列的可逆性。
根据上文分析,时间序列模型的时域特性见表 1。
| 表 1 时间序列模型的特性 Table 1 Characteristics of Time Series Model |
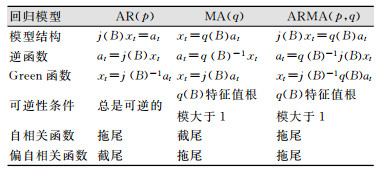 |
1.3 时间序列建模一般步骤
时间序列建模要求数据平稳、正态、零均值,对于实际测量的数据往往不能直接满足此条件,还需要对数据进行预处理,再进行建模,具体步骤如下:①根据原始测量数据的时间序列图,以及其自相关函数和偏自相关函数,用相应的检验方法检验其方差、趋势及其季节性变化规律,对序列的平稳性进行判断;②如果序列为非平稳序列,需要进行平稳化检验;③对差分后的时间序列进行模型识别,综合确定相应的模型;④对模型进行参数估计,根据相应参数建立模型方程;⑤进行模型检验及优化;⑥建模完成后,利用已通过检验的模型进行预测分析。
2 实例分析本次实例是基于我国西南地区某变形监测项目,从施工开始到运营期间对每个点进行定期观测,记录下建筑物的变形状况。为了说明时间序列建模过程,本文就某一点的数据进行时间序列分析。
2.1 时间序列预处理本次实验对该变形监测点X01进行了54个周期的等时间间隔观测,用前44期观测值进行建模分析,用后10期数据来验证时间序列分析模型预测的准确性。为了检验数据的平稳性,绘制了该点的序列图,由图 1可以看出变形数据具有明显的线性变化趋势,呈现下降趋势,属非平稳序列。对其进行一阶差分,绘制一阶差分序列图,如图 2所示。从图 2可以看出,序列符合平稳、正态、零均值的特性。
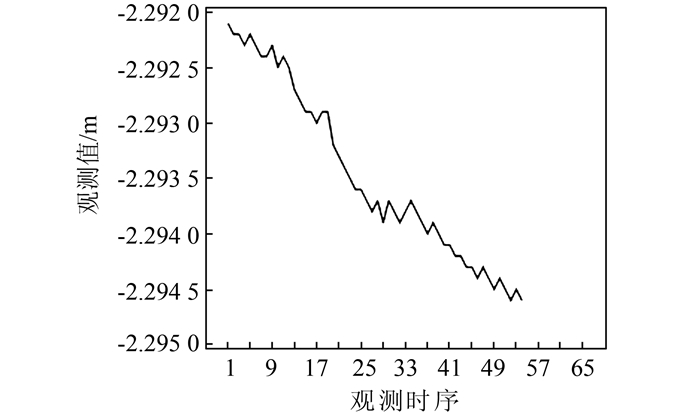 |
| 图 1 X01点的序列图 Figure 1 Time Series Graph of X01 |
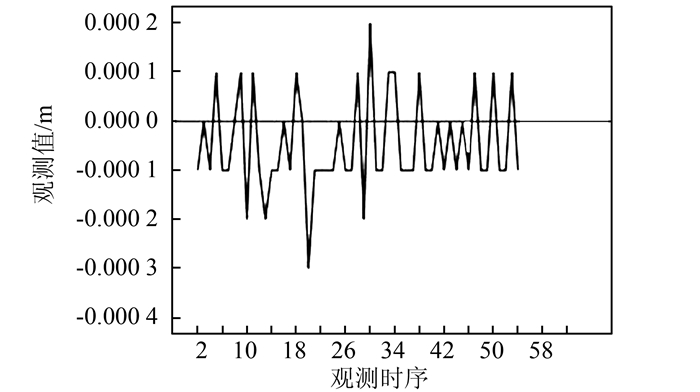 |
| 图 2 一阶差分图 Figure 2 First-order Differential Time Series Graph |
2.2 模型识别与定阶
经过时间序列的预处理工作,差分序列满足了平稳非白噪声序列,现通过绘制序列的自相关系数与偏自相关系数进一步确定拟合模型的结构,在样本观测值有限时,可采用动态数据系统(DDS)方法判别模型阶数,并对模型的适用性进行检验,图 3、图 4为自相关、偏自相关系数图。
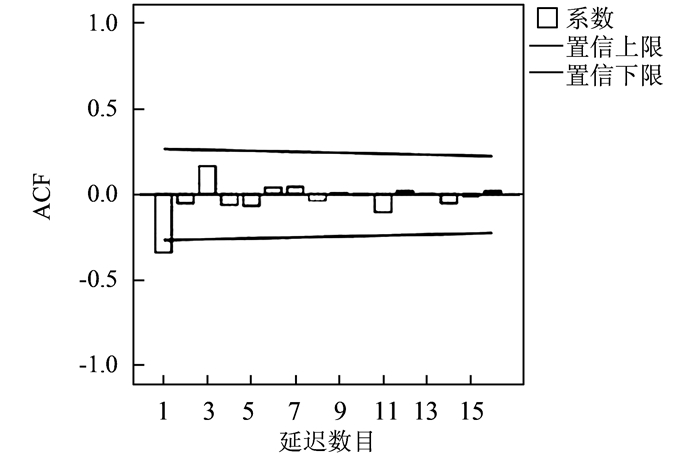 |
| 图 3 序列自相关图 Figure 3 Auto-correlation Graph |
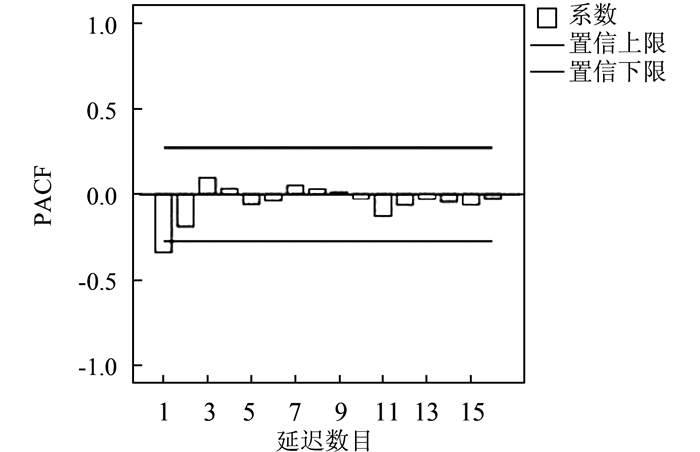 |
| 图 4 序列偏自相关图 Figure 4 Partial Auto-correlation Graph |
从图 3、图 4可以看出,一阶延迟过后,自相关系数都在2倍标准差以内有小幅波动视其均为拖尾。自相关图延迟系数在3阶、11阶时相对较大,而偏自相关图在2阶、3阶、11阶的时候延迟系数相对较大。对模型适用性进行检验(信息量最小准则;DW统计量范围准则;模型精确准则,即残差平方和RSS等),经过比较,模型ARIMA (3, 1, 3)显著有效,对序列适应性更强, 故选其为最优模型来进行原始数据拟合。
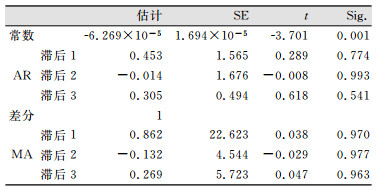
2.3 参数估计及模型检验在最小二乘估计理论下,经过计算,参数估计结果如表 2所示。
| 表 2 ARIMA (3,1,3)模型参数估计结果/m Table 2 Results of ARIMA (3, 1, 3) Parameter Estimation/m |
 |
为了避免或减少人为因素导致在建模中模型识别与定阶不准的问题,还需对模型进行模型检验及优化,常用的检验方法有AIC准则和SBC准则,模型的优化与检验是同时进行的,在满足模型参数显著与残差白噪声的前提下,该模型都是相对最优模型。如图 5为ARIMA (3, 1, 3)模型拟合图。
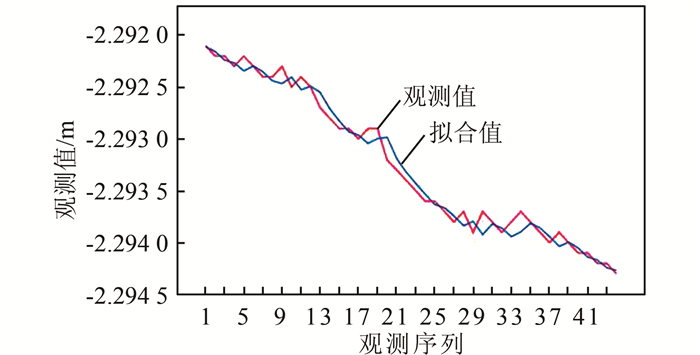 |
| 图 5 ARIMA (3, 1, 3)模型拟合图 Figure 5 Fitting Graph of ARIMA (3, 1, 3) Model |
2.4 时间序列预测结果
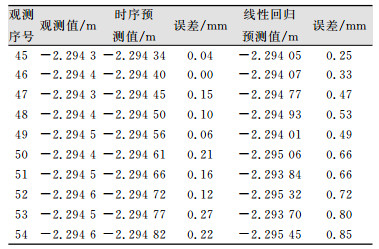
根据拟合模型ARIMA (3, 1, 3),对原始数据进行时间序列预测,同时将预测数据与实际观测数据以及线性回归模型预测结果进行对比,见表 3。
| 表 3 X01点观测值与预测值的比较 Table 3 Comparison of Observed and Predicted Values of X01 |
 |
综合实测数据以及模型预测可得出以下结论:
1) 时间序列预测结果与实际观测值非常接近,模型拟合精度高,同时随着预测期数的增加,误差有增大的趋势,但10期的预测误差都在0.3 mm以内,仍达到了比较高的预测精度,预测效果令人满意。
2) 线性回归模型预测值总在实际值之间上下浮动,幅度较均匀,随着预测期数的增加,其预测精度也逐渐降低,预测误差达到了0.85 mm,相比时间序列预测存在较大误差。
3) 在短期预测中,参与建模的样本观测值一般较少,相比之下,时间序列模型的预测精度高,且具有良好的稳定性与可靠性。
3 结束语1) 时间序列分析是对变形测量数据分析的常用处理方法,本文基于统计分析软件的辅助,实现了序列建模,并以较高的精度对序列数据进行拟合与预测,切实反映了建筑物的变化规律。
2) 运用时间序列方法进行建模与预测时,尽可能地避免个人经验不足导致模型识别不准,同时需要足够多的原始数据,从而降低个别监测质量不高的点的影响。
3) 随着预报期数的增加,预测精度逐渐下降,所以需要及时加入新观测值,从而实现短周期高精度的预测,及时掌握建筑物的变形情况。
| [1] |
黄声享, 尹晖.
变形监测数据处理[M]. 武汉: 武汉大学出版社, 2010 .
Huang Shengxiang, Yin Hui. Deformation Monitoring Data Processing[M]. Wuhan: Wuhan University Press, 2010 . |
| [2] |
刘娜, 栾元重, 黄晓阳. 基于时间序列分析的桥梁变形监测预报研究[J].
测绘科学,2011,36(11) : 46–48.
Liu Na, Luan Yuanzhong, Huang Xiaoyang. Bridge Deformation Monitoring and Forecasting Based on Time Series Analysis[J]. Science of Surveying and Mapping,2011,36(11) : 46–48. |
| [3] |
王刘准, 邱卫宁, 花向红, 等. 小波时间序列分析在高铁沉降变形中的应用[J].
测绘地理信息,2013,38(4) : 45–51.
Wang Liuzhun, Qiu Weining, Hua Xianghong, et al. The Application of Time Series Analysis Based on the Wavelet in the Deformation of High-speed Rail[J]. Journal of Geomatics,2013,38(4) : 45–51. |
| [4] |
吴芸芸, 左廷英, 朱建军. 时间序列在变形监测中的应用[J].
工程勘察,2012,(1) : 69–72.
Wu Yunyun, Zuo Tingying, Zhu Jianjun. Application of Time Series Analysis in the Deformation Monitoring[J]. Geotechnical Investigation and Surveying,2012,(1) : 69–72. |
| [5] |
肖枝洪, 郭明月.
时间序列分析与SAS运用[M]. 武汉: 武汉大学出版社, 2009 .
Xiao Zhihong, Guo Mingyue. Time Series Analysis and SAS Application[M]. Wuhan: Wuhan University Press, 2009 . |
| [6] |
沈云中, 陶本藻.
实用测量数据处理方法[M]. 北京: 测绘出版社, 2012 .
Shen Yunzhong, Tao Benzao. Practical Methods for Surveying Data Processing[M]. Beijing: Surveying and Mapping Press, 2012 . |
| [7] |
郑加柱, 郭斐. 变形监测数据的时间序列分析[J].
森林工程,2008,(4) : 50–53.
Zheng Jiazhu, Guo Fei. Time Series Analysis of Deformation Monitoring Data[J]. Forest Engineering,2008,(4) : 50–53. |
| [8] |
刘艳萍, 贾东峰, 程效军. 时间序列分析在建筑物变形监测中的应用[J].
勘察科学技术,2010,(6) : 46–49.
Liu Yanping, Jia Dongfeng, Cheng Xiaojun. Application of Time Series Analysis in Buildings Deformation Monitoring[J]. Site Investigation Science and Technology,2010,(6) : 46–49. |
| [9] |
杨叔子, 吴雅, 轩建平.
时间序列分析工程应用[M]. 武汉: 华中科技大学出版社, 2007 .
Yang Shuzi, Wu Ya, Xuan Jianping. Time Series Analysis in Engineering Application[M]. Wuhan: Huazhong University of Science and Technology Press, 2007 . |
 2016, Vol. 41
2016, Vol. 41

