| 利用植被光谱数据和Stacking算法识别油菜关键生长发育期 |
油菜是我国主要的经济作物之一,油菜关键生长发育期的信息对田间管理,观赏时间,产量评估等具有重要的意义[1]。油菜关键生育期分为叶期、花期、角果期、成熟期。叶期为主要生长时期,占生育期总时长的一半以上,花期是营养生长和生殖生长最旺盛的时期,角果期为花期结束到角果籽粒成熟的一段时期,在角果期初期,角果为绿色,随着角果的逐渐成熟进入成熟期。
遥感进行生育期识别常见的方法归纳为以下6种:①植被指数阈值法,设定植被指数阈值来确定生育期[2];②滑动移动平均法,对植被指数的时间序列曲线进行平滑,利用平滑后延迟的曲线与原始曲线的交点表示生长季节的开始和结束[3];③梯度法,利用植被指数的时间序列曲线的梯度信息,根据极值点作为作物的关键生育时期[4];④谐波分析法,对植被指数时间序列曲线进行傅里叶变换或小波变换等去噪方法,剔除植被指数时间序列中的噪声对结果的影响,然后对作物的生育期进行识别[5];⑤光谱空间方法,根据不同的生育时期在光谱空间中的聚类现象,对作物生育进行区分[6];⑥机器学习方法,通过构造有效特征进行分类器的训练,对作物的生育期进行区分[7]。
植被指数阈值考虑了植被指数曲线的特征,但对阈值的选择较为敏感;基于时序植被指数的方法需要长时间序列的反射率信息,对于较低时间分辨率的数据源需要进行差值处理,带来一定的误差。光谱空间法对于油菜等花期特征异常明显的作物,在光谱空间中难以区分。机器学习方法广泛的应用于分类、回归等问题,不同的机器学习算法模型,依据不同规则进行学习。然而,真实样本的假设空间不在当前算法的假设空间中,同时从计算的方面来看,机器学习算法往往会陷入局部最优解。因此单一的机器学习算法对未知样本的泛化能力较差。为了解决这一问题,本文使用Stacking算法,将多种机器学习算法进行融合学习,以期提高油菜生育期识别的能力。
1 Stacking算法Stacking算法是基于Worlpert[8]提出的Stacked Generalization框架,该框架由两层结构组成,从原始训练集中学习的若干个基分类器作为第一层,每个基分类器的结果组成一个新的数据集,用于训练第二层的次级分类器。为了避免引起过拟合,同时选择不同算法的最优超参数,在生成基分类器时采用k折交叉验证将训练样本分层采样划分成k个大小相同的集合D1, D2, …, Dk。每次选择k-1个集合Dj(j=1, 2…k)作为训练集,剩余的作为测试集D′j。基分类器通过k折交叉验证选出使分类结果最优的N个分类器ht(t=1, 2, …, N)。将测试集D′j的结果ht(D′j)作为次级分类器的训练样本,以训练次级分类器,次级分类器的分类结果作为最终的分类决策。
本文提取油菜生育期中的冠层光谱信息作为特征,采用k近邻[9](k-nearest neighbor, KNN)、支持向量机[10](support vector machines, SVM)、随机森林[11](random forest, RF)、梯度提升决策树[12](gradient boosted decision trees, GBDT)和人工神经网络[13](artificial neural networks, ANN)等5种常用的机器学习算法作为基分类器。
2 油菜生长发育期识别与评价 2.1 研究区域与数据本文选取湖北省武汉市和武穴市两处典型冬油菜种植区域作为研究区域。武汉市油菜实验田(114°21′N,30°33′E)分为9个小区,每个小区面积为9 m2(3 m×3 m)。武穴市梅川县油菜实验田(115.35°N, 30.06°E)分为24个小区,每块小区的面积为30 m2(15 m×2 m)。以25%植株开花认为从叶期进入花期,75%以上花调零则进入角果期,全区75%以上角果呈枇杷黄色进入成熟期为标准,实地观察的油菜的生长状况,目视解译得到油菜真实生育期。
SKYE(SKR 1860, SKYE Instruments Ltd., Llandrindod Wells, UK)由上下两个辐射计组成,每个辐射计有4个通道,其波段范围分别为:绿(531.2~570.8 nm)、红(635.1~670.8 nm)、红边(703.9~730.1 nm)和近红(838.4~876.4 nm)。上辐射计有余弦矫正器,具有180°的视角,采集太阳下行辐射在4个波段的辐照度;下辐射计无余弦矫正器,具有25°的视角,采集植被冠层反射的辐亮度。SKYE仪器被安置于武汉市实验田距离地面4 m的金属支架上,能够实时采集其镜头下方25°视场角下的数据。
为了移除由于快速的辐射变化所引起的数据方差扰动,辐射计被设计为每隔一个小时记录一次辐射平均值,其波段i在1 h中的平均反射率ρi为下辐射计上行的1 h辐亮度(RUW(λ))和上辐射计下行的1 h辐照度(IDW(λ))比值,如式(1)所示。
| ${\rho _i} = \left[ {{R_{UW\left( \lambda \right)}} \times C{C_{UW(\lambda )}}} \right] \times {\left[ {{I_{DW(\lambda )}} \times C{C_{DW(\lambda )}}} \right]^{ - 1}} $ | (1) |
式中,CCUW(λ)是在λ波段对于UW(mV)的校准系数;CCDW(λ)是对于DW(mV)的校准系数。
使用ASD(FieldSpec 4, ASD Inc., Co., UAS)实地获取的高光谱数据进行验证。其光谱范围为:350~2 500 nm,在可见光和近红外部分的光谱分辨率为3 nm,红外部分的光谱分辨率为8 nm。
使用DJI S1000型六旋翼无人机(unmanned aerial vehicle,UAV)进行油菜不同时期的数据获取,其搭载了6个微型Mini-MCA相机(Mini-MCA 6, Terracam Inc., Chatsworth, CA, USA)。利用地面标准反射板,采用线性模型对影像进行辐射定标,将影像的数字信号(DN值)转化成光谱反射率。
2.2 数据处理SKYE根据上下两个辐射计的比值计算反射率,当太阳天顶角超过70°时,由于更高的镜面反射率对二向反射系数的贡献,冠层反射率会剧烈变化。图 1是由SKYE计算得来的4波段反射率在一天中的变化曲线,11:00~14:00时反射率的变化较小,趋近于稳定。因此选择每天11:00~14:00时的反射率数据作为4个波段有效的冠层光谱反射率。
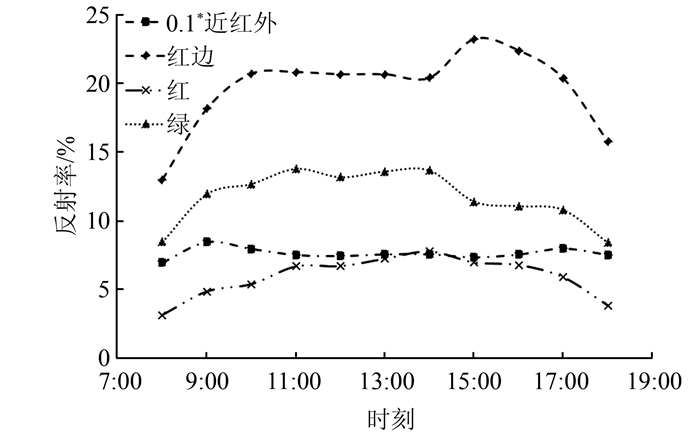 |
| 图 1 冠层光谱反射率的日变化 Fig.1 Diurnal Reflectance of Canopy Reflectance |
将11:00~14:00时的光谱反射率取平均,获得每日4个波段的油菜冠层反射率。通过实地观测的目视解译进行不同时期的划分(图 2)。随着移栽油菜的生长,4个波段的反射率都会出现不同的变化。因此以绿、红、红边和近红外波段的反射率信息的原始数据作为特征能够很好的表现不同生育期。
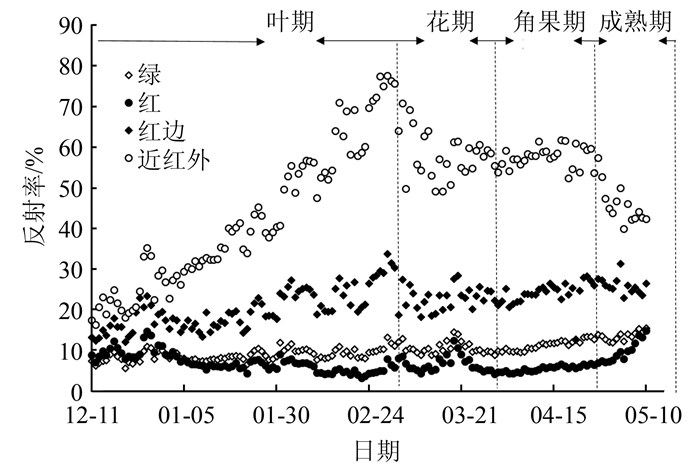 |
| 图 2 油菜全生育期的每日反射率变化 Fig.2 Daily Reflectance in the Entire Rapeseed Growing Season |
2.3 结果与评价
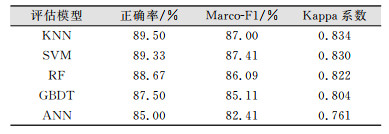
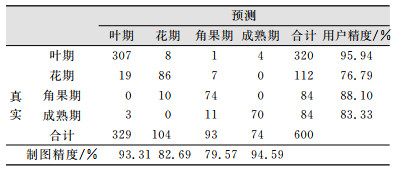
在油菜的整个生长期中共采集到150 d数据,选取每天11:00~14:00时的光谱数据共600个训练样本,对所有的样本进行归一化处理去除不同波段的尺度差异。通过10折交叉验证在训练集中选择KNN、SVM、RF、GBDT、ANN算法的最优模型参数。不同算法的识别结果显示KNN算法最优,识别正确率最高达89.50%(表 1)。KNN算法的叶期识别正确率最高达95.94%(表 2),花期正确率最低(76.79%),19个花期的数据被错分成叶期,这是由于花期和叶期相邻,在光谱空间中的聚类较近,使用KNN算法是容易造成错分。
| 表 1 单一分类器模型油菜关键生育期识别结果 Tab.1 Accuracy for Remote Detection of Rapeseed Phenology Using Single Classifier Model |
 |
| 表 2 KNN算法油菜关键生育期识别混淆矩阵 Tab.2 Confusion Matrix of Rapeseed Phenology Recognition Using KNN Algorithm |
 |
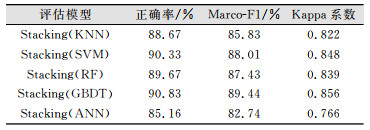
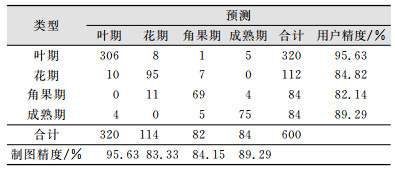
在Stacking算法的第二层采用不同算法作为次级分类器,Stacking(KNN)表示使用KNN算法作为次级分类器的结果。不同算法结果如表 3所示,其中,最优的识别正确率为使用GBDT作为次级分类器(90.83%),其区分不同油菜生育时期均达到82%以上(表 4)。
| 表 3 Stacking算法识别油菜关键生育期识别结果 Tab.3 Accuracy for Remote Detection of Rapeseed Phenology Using Stacking Algorithm |
 |
| 表 4 Stacking(GBDT)油菜关键生育时期识别混淆矩阵 Tab.4 Confusion Matrix of Rapeseed Phenology Detection Using Stacking (GBDT) Algorithm |
 |
比较表 1和表 3可知,Stacking算法的结果普遍高于单一分类器。使用单一分类器时,所有算法均有85%以上的正确率,其中KNN的识别效果最好,达到89.50%。使用融合分类器时,Stacking(GBDT)的精度最高,达到90.83%,高出单一分类器精度1.33%。
为了验证Stacking算法在不同平台下的泛化能力,使用全部的SKYE数据训练Stacking模型。测试集为单独的ASD、UAV和跨平台(ASD-UAV)数据。不同算法在不同的数据集中的正确率如图 3所示。总体地面ASD的关键生育期识别精度要高于低空平台UAV数据的精度,这是由于无人机从空中采集数据,其辐射定标、几何校正等都会给反射率的计算带来影响,使识别效果变差。Stacking算法的精度优于所有的单个分类器,表明其具有良好的泛化能力。
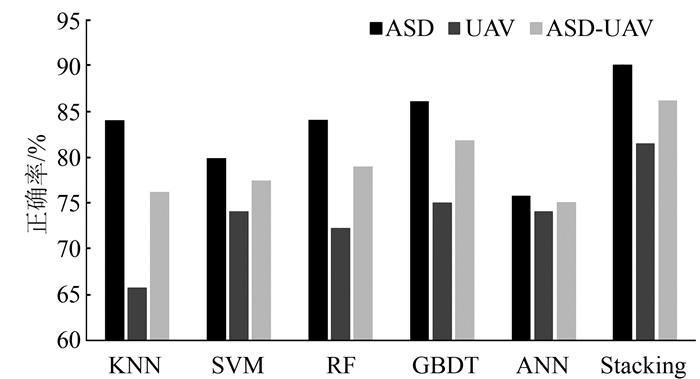 |
| 图 3 不同算法不同平台的正确率对比 Fig.3 Accuracy Comparison for Detecting Rapeseed Phenology Stages Using Different Algorithms Retrieved by Different Platforms |
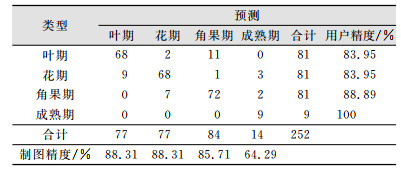
Stacking算法对跨平台数据集进行识别的混淆矩阵如表 5所示,油菜叶期、花期、角果期和成熟期4个生育时期的精度均达到80%以上。误识别情况主要出现在叶期和花期,叶期较容易被误认为角果期,误识别比例达到13.58%,主要是因为叶期和角果期的光谱反射率较为相似(图 3),仅使用反射率信息作为特征会带来一定的误差。花期被误识别为叶期(11.11%),因为花期和叶期相邻,花期的开始日期与人为定义的花覆盖率有关,受主观影响较大。其他生育期的识别情况较为理想,总体的精度86.11%,Kappa系数0.8。
| 表 5 跨平台数据的油菜生育时期识别混淆矩阵 Tab.5 Confusion Matrix of Rapeseed Phenology Detection Using Cross-platform Data |
 |
3 结束语
采用常用的机器学习以及Stacking算法对油菜的关键生育期进行识别。结果表明,Stacking算法效果最优。在同源数据中,Stacking算法比最好的单一分类器(KNN)提升1%的正确率,在不同源数据中,Stacking算法比最好的单一分类器(GBDT)提升5%的正确率。本文提出的方法能够对生育期精确识别,为油菜的田间管理、观赏时间预测、产量评估等提供参考。此外,本文的方法可推广至卫星影像提取大面积物候信息, 可为其他作物的生育期识别提供新的思路。
| [1] |
龚龑, 肖洁, 侯金雨, 等. 基于无人机遥感混合光谱分析的油菜估产模型[J]. 测绘地理信息, 2017, 42(6): 40-45. |
| [2] |
Guo L, An N, Wang K. Reconciling the Discrepancy in Ground and Satellite-Observed Trends in the Spring Phenology of Winter Wheat in China from 1993 to 2008[J]. Journal of Geophys Research:Atmospheres, 2016, 121(3): 1027-1042. DOI:10.1002/2015JD023969 |
| [3] |
Schwartz M D, Reed B C, White M A. Assessing Satellite-Derived Start-of-Season Measures in the Conterminous USA[J]. International of Journal Climatology, 2002, 22(14): 1793-1805. DOI:10.1002/joc.819 |
| [4] |
张峰, 吴炳方, 刘林成, 等. 利用时序植被指数监测作物物候的方法研究[J]. 农业工程学报, 2004, 20(1): 155-159. DOI:10.3321/j.issn:1002-6819.2004.01.038 |
| [5] |
Sun Huasheng, Huang Jinfeng, Peng Dailiang. Detecting Major Growth Stages of Paddy Rice Using MODIS Data[J]. Journal of Remote Sensing, 2009, 13(6): 1130-1137. |
| [6] |
Nguy-Robertson A, Gitelson A, Peng Y, et al. Continuous Monitoring of Crop Reflectance, Vegetation Fraction and Identification of Developmental Stages Using a Four-Band Radiometer[J]. Agronomy Journal, 2013, 105(6): 1769-1779. DOI:10.2134/agronj2013.0242 |
| [7] |
Almeida J, dos-Santos J A, Alberton B, et al. Applying Machine Learning Based on Multiscale Classifers to Detect Remote Phenology Patterns in Cerrado Savanna trees[J]. Ecological Informatics, 2014, 23: 49-61. DOI:10.1016/j.ecoinf.2013.06.011 |
| [8] |
Wolpert D H. Stacked Generalization[J]. Neural Networks, 1992, 5(2): 241-259. DOI:10.1016/S0893-6080(05)80023-1 |
| [9] |
Cover T M, Hart P E. Nearest Neighbor Pattern Classification[J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27. |
| [10] |
Cortes C, Vapnik V. Support-vector Networks[J]. Machine Learning, 1995, 20(3): 273-297. |
| [11] |
Breiman L. Random Forest[J]. Machine Learning, 2001, 45(1): 5-32. |
| [12] |
Friedman J H. Greedy Function Approximation:A Gradient Boosting Machine[J]. Annals of Statistics, 2001, 29(5): 1189-1232. DOI:10.2307/2699986 |
| [13] |
McCulloch W S, Pitts W. A Logical Calculus of the Ideas Immanent in Nervous Activity[J]. Bulletin of Mathematical Biology, 1990, 52(1/2): 95-115. |
 2019, Vol. 44
2019, Vol. 44

