| 地铁沉降数据的时间序列分析与研究 |
2. 成都理工大学地球科学学院,四川 成都, 610059
2. College of Earth Sciences, Chengdu University of Technology, Chengdu 610059, China
近年来,对变形数据分析和预报方法的研究很多,主要有时间序列分析法、BP神经网络法、回归分析法、卡尔曼滤波法、灰色系统理论、小波分析等[1]。时间序列分析法是研究较多的一种动态数据处理方法,具有表达简洁、短期预报等优点。该方法通过对按时间序列排列的、随时间变化且相互关联的数据序列进行分析,找出反映事物随时间的变化规律,从而对数据变化趋势做出正确分析和预报[2]。基于平稳时间序列的分析理论,本文对西安地铁五路口站的地质沉降数据进行研究,分别对沉降观测值和沉降量进行分析、建模,并对模型的拟合精度和对变形数据预测的准确度进行分析。
1 时间序列模型与建模 1.1 时间序列模型时间序列分为平稳时间序列和非平稳时间序列两类。平稳时间序列模型有自回归(auto-regressive,AR)模型、移动平均(moving average,MA)模型以及自回归移动平均(auto-regressive moving average,ARMA)模型3种基本类型[3, 4]。
1) 如果某时间序列是它的前期值和随机项的线性函数,则此时间序列Xt可表示为:
| $ {X_t} = {\phi _1}\;{X_{t-1}} + \cdots + {\phi _p}\;{X_{t-p}} + {\varepsilon _t} $ | (1) |
式中,Xt为t时刻观测值,其中含有p个加权系数ϕi,称为自回归系数;εt是白噪声序列。故称该时间序列是p阶自回归序列,记为AR(p)。
2) 如果某时间序列是它的当期和前期的随机误差项的线性函数,则此时间序列Xt可表示为:
| $ {X_t} = {\varepsilon _t}-{\theta _1}{\varepsilon _{t-1}}-\cdots - {\theta _q}{\varepsilon _{t - q}}\; $ | (2) |
式中,Xt为t时刻观测值,其中含有q个加权系数θi;εt是白噪声序列。故称该时间序列是q阶移动平均序列,记为MA(q)[5]。
1.2 时间序列建模 1.2.1 序列的平稳性检验时间序列模型是建立在随机序列是平稳序列假设基础上的,因此建立模型之前,首先要进行随机序列的平稳性检验[6]。
如果时间序列的样本自相关系数缓慢下降,表明序列不是平稳序列,而存在趋势项,应通过差分的办法消除; 若自相关系数具有振荡下降的特点,或具有很大的波动性,或近似含有周期性中的任意特点,表明序列存在周期项或季节影响,应通过延迟d步差分来消除[7]。样本的自相关函数为:
| $ {\rho _k} = \frac{{{r_k}}}{{{r_0}}}\; = \frac{{\sum \left( {{z_t}{\rm{-}}\bar z} \right)\left( {{z_{t + k}}{\rm{-}}\bar z} \right)}}{{\sum {{\left( {{z_t}{\rm{-}}\bar z} \right)}^2}}}\; $ | (3) |
式中,ρk为样本自相关函数;zt为t时刻观测值; zt+k为t+k时刻观测值。
1.2.2 模型的确定时间序列平稳性检验后要进行模型确定。Box-Jenkins模型识别方法是根据时间序列数据自相关、偏自相关函数的特征来确定模型的类型[8]。
若平稳时间序列的自相关函数满足样本(偏)自相关系数在最初的d阶明显大于两倍标准差范围,而后几乎95%的自相关系数都落在两倍标准差的范围以内,而且通常由非零自相关系数衰减为小值波动的过程非常突然,这时,通常视为(偏)自相关系数截尾,否则称偏自相关函数为拖尾[1]。若样本的自相关函数在d阶之后截尾,则判断序列为MA模型;若样本的偏自相关函数在d阶之后截尾,则判断序列为AR模型;当两者都不截尾而呈现拖尾特性时,则判断其为ARMA模型[9]。
1.2.3 模型的定阶与参数估计模型的定阶方法主要有偏相关函数法、AIC(Akaike information criterion)准则法、F检验法、BIC(Bayesian information criterion)准则法、FPE(final prediction error)准则法等[10]。对于ARMA(n, m)模型,AIC准则函数定义为:
| $ {\rm{AIC}}\left( {n, m} \right) = {\rm{ln}}\hat \sigma _a^2 + 2\left( {n + m} \right)/\left( {N{\rm{-}}n} \right)\; $ | (4) |
式中,
在选定某种模型如AR、MA、ARMA模型后,要对模型的未知参数进行估计,估计的方法与数理统计中的参数点估计方法类似,包括相关矩估计、最小方差估计、极大似然估计、最小二乘估计、最大熵估计等[1, 10, 11]。本文采用最小二乘估计法[7, 10]。
1.2.4 模型检验模型估计之后,应进行模型适应性检验,检验模型中的干扰项是否满足正态白噪声的假设,应分别检验残差项是否为近似正态及近似白噪声。
模型建成之后,需要进行统计学检验。通常采用R2、F作为检验统计量,以此判定估计参数、模型拟合优度和方程的统计显著性。
1.3 模型预测在实际应用中,进行时间序列分析最主要的目的就是进行预测,也就是根据所建立的模型对未来一段时间内可能发生的趋势进行预测和预报[4]。AR(p)模型的d步预测计算公式为:
| $ {X_{k + d}} = \sum\limits_{j = 1}^p {{a_j}\;{X_{k + d-j}} + {\varepsilon _{k + d}}} \; $ | (5) |
式中,εk+d=Xk+d-Xk+d-1。
2 实例分析 2.1 工程基本情况五路口站是西安地铁1号线与4号线的换乘站。4号线车站位于解放路与东五路十字南侧,成南北走向,布置在解放路下方。1、4号线车站呈T字岛换乘,1号线为地下两层岛式站台车站,4号线为地下3层岛式站台车站。主体结构基坑为半幅铺盖顺筑方案(西侧基坑半幅铺盖),采用钻孔灌注桩和内支撑的基坑支护,桩间设单根二重管旋喷桩止水帷幕,明挖顺作法施工。
2.2 数据处理与模型建立施工期间对39个变形监测点共进行了150期等时间间隔观测沉降,观测点布设如图 1所示。对数据取等时间间隔处理,得到50期等时间间隔观测数据。本文选择靠近基坑的D12号点及其前40期数据作为样本数据,分别对沉降观测值和沉降量进行时间序列建模分析,以此来对后期数据进行预测。根据预处理后的数据绘制沉降数据随时间的分布曲线图,如图 2所示。
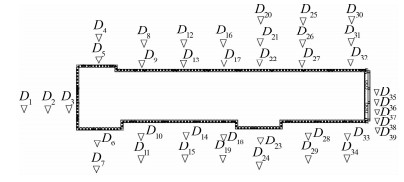 |
| 图 1 沉降监测点分布图 Figure 1 Distribution of Settlement Monitoring Points |
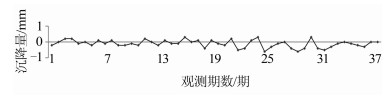 |
| 图 2 沉降量随时间变化图 Figure 2 Change of Settlement with Time |
2.2.1 时间序列的平稳性检验
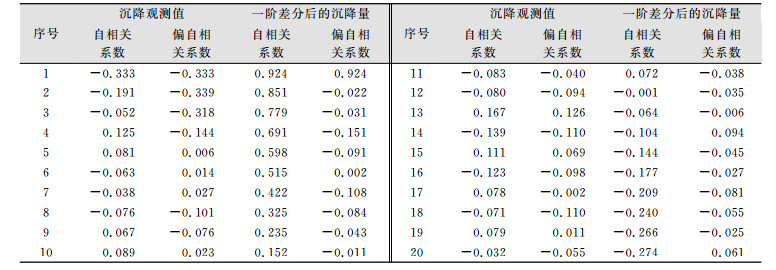
根据预处理后的数据计算样本自相关系数和偏自相关系数。表 1为沉降观测值计算结果和对沉降量进行一阶差分后的计算结果。通过一阶差分处理后,自相关系数随着序号的增大,数值迅速趋近于0,并在0附近波动。由此得出,该序列可以认为是平稳时间序列。
| 表 1 沉降观测值和沉降量一阶差分后的自相关系数和偏自相关系数 Table 1 Auto-Correlation Coefficients and Partial Auto-Correlation Coefficients of Settlement Observation and the Settlement After First Order Difference |
 |
2.2.2 模型的确定与求解
由表 1中自相关系数和偏自相关系数的计算结果可以看出,沉降观测值序列自相关系数拖尾,偏自相关系数一阶截尾,初步认为序列符合AR(p)模型。根据AIC定阶准则,计算AR(1)、AR(2)、AR(3)的AIC。当p=1时,AIC=0.987 1为最小值, 故该序列符合AR(1)模型。根据最小二乘估计法求得AR(1)模型系数,得到AR(1)模型,并绘制拟合图如图 3(a)所示。
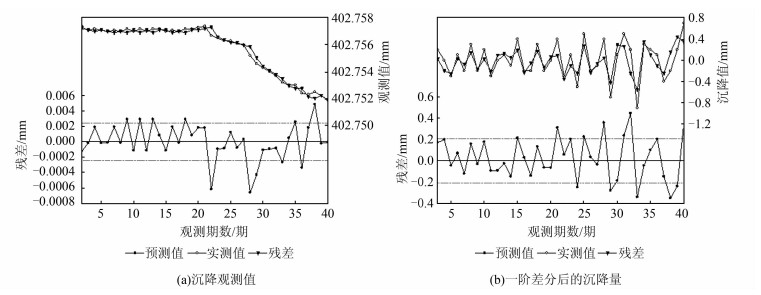 |
| 图 3 拟合值与原始预测值比较 Figure 3 Comparison of the Fitting Values and Prediction Values |
由表 1知,一阶差分处理后的沉降量序列偏自相关系数和自相关系数均拖尾,初步确定为ARMA(p,q)模型,用AIC定阶准则确定为ARMA(1, 1)模型,并绘制拟合图见图 3(b)。可以看出,时间序列分析对沉降观测值的拟合精度要优于对沉降量的拟合精度。
2.3 模型的检验和比较模型建立后对残差序列进行白噪声检验,看出偏自相关系数和自相关系数都没有显著趋于0,Q统计量的p值都远远大于0.05,因此可以认为残差序列为白噪声序列,模型信息提取比较充分。常数和滞后一阶参数的p值都很小,参数显著,因此整个模型比较精简,模型较优。
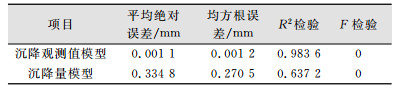
计算模型的拟合平均绝对误差、均方根误差、拟合优度检验(R2检验)和方程显著性检验(F检验)值如表 3所示。由各项统计值可以看出,时间序列分析对沉降观测值的拟合精度为0.983 6, 要明显优于对沉降量的拟合精度。
| 表 3 模型检验表 Table 3 Model Check Table |
 |
2.4 模型预测
根据以上结论,选择沉降观测值序列的AR(1)模型对后8期的沉降量进行预测,预测值与实测值的残差如表 4所示。
| 表 4 模型预测值与实测值的残差比较/mm Table 4 Difference Comparison of the Predictive Values and the Measured Values/mm |
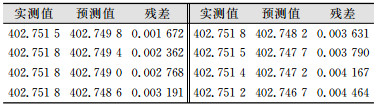 |
根据表 4可以得出,随着预测期数的增加,模型的精度有下降趋势,可见时间序列模型适合短期预测。通过残差可以看出,时间序列在预测变形的准确度上还不够,因此只适用于沉降数据的短期趋势预测。
3 结束语本文使用时间序列分析的方法,对西安地铁五路口站的沉降数据进行建模分析。分析结果表明,时间序列分析能够预测短时间内的沉降量;时间序列模型的预测精度随预测期数的增加而减小,适合做短期预测;时间序列模型进行沉降预测的准确度不高,因此只适合做短期趋势预测。
| [1] | 何书元. 应用时间序列分析[M]. 北京: 北京大学出版社, 2004 |
| [2] | 刘大杰, 陶本藻. 实用测量数据处理方法[M]. 北京: 测绘出版社, 2000 |
| [3] | 吴怀宇. 时间序列分析与综合[M]. 武汉: 武汉大学出版社, 2004 |
| [4] | 王刘准, 邱卫宁, 花向红, 等. 小波时间序列分析在高铁沉降变形中的应用[J]. 测绘地理信息, 2013, 38(4): 45–47 |
| [5] | 叶尔骅, 张德平. 概率论与随机过程[M]. 北京: 科学出版社, 2005 |
| [6] | 陈青, 罗志清, 吴芸芸. 时间序列在变形监测中的应用[J]. 江西科学, 2011, 29(2): 216–218 |
| [7] | 赵仲荣, 袁树才, 张立群. 建筑物差异沉降的时间序列分析与预报[J]. 工程勘察, 2010, 38(1): 73–76 |
| [8] | 刘娜, 栾元重, 黄晓阳, 等. 基于时间序列分析的桥梁变形监测预报研究[J]. 测绘科学, 2011, 36(6): 46–48 |
| [9] | 徐爱功, 李娜, 张涛. 时间序列分析在地铁沉降观测中的应用[J]. 测绘科学, 2013, 38(5): 57–60 |
| [10] |
冯小磊. 边坡变形监测模型和稳定性评价的研究及应用[D]. 南京: 河海大学, 2006 |
| [11] | 王岩, 隋思涟, 王爱青. 数理统计与MATLAB工程数据分析[M]. 北京: 清华大学出版社, 2006 |
 2018, Vol. 43
2018, Vol. 43

