| 基于豪斯霍尔德变换的三维空间柱面拟合 |
在工业、工程检测和逆向工程中,曲面拟合是经常遇到的问题。一般实物在空间的模型都有着严格的数学公式表达,通过扫描获取实物表面点的三维坐标,可以拟合出实物表面在空间坐标系中的几何方程[1, 2],这对于发现实物的整体形变以及生成模型设计CAD图纸是至关重要的。谷川等[3, 4]提出了采用遗传算法进行曲面拟合,并且通过工程实例说明了该算法的有效性,但是对于柱面这一类的空间曲面进行坐标平移旋转以及标准曲面表达参数的求取存在一定的困难。张益泽等[5]利用圆柱的几何原理列误差方程,并对其做平方变换,相较于谷川的方法较为简单,但要加两个限制条件,而且要迭代两次。田晓等[6]利用坐标转换的方法达到减少了参数的目的,但也仅仅是对圆柱面进行了拟合。王解先[7, 8]针对工业测量中的二次曲面拟合提出了按特征值、旋转角和平移量为参数拟合二次曲面,其对于旋转矩阵是分别求3个旋转角的3个旋转矩阵的乘积,不能直接得到旋转矩阵。据此,本文提出了基于豪斯霍尔德变换的三维空间柱面拟合法,豪斯霍尔德变换可以直接得到旋转矩阵,将提高拟合的效率,通过豪斯霍尔德变换将柱面的轴向转换到与测量坐标系Z轴平行,点云投影到二维平面,再拟合投影的曲线,最后拓展到三维空间达到柱面拟合,为后面点云三维建模中一般柱面的建模提供一种新的方法,并结合实例说明该方法可行且精度可靠。
1 三维空间柱面拟合的数学模型常见的三维空间柱面包括圆柱面、椭圆柱面、抛物柱面和双曲柱面[9]。这些柱面在一个测站的数据在二维平面都可以用式(1)来表达。
| $ y = {a_0} + {a_1}x + {a_2}{x^2} $ | (1) |
一般地,在Rn中,将向量x映射为关于“与单位向量u正交的n-1维子空间”对称的向量y的镜像变换定义如下:设单位向量ω∈Rn,称R=E-2ωωT为豪斯霍尔德矩阵(初等反射矩阵),由豪斯霍尔德矩阵确定的线性变换成为豪斯霍尔德变换(初等反射变换、镜像变换或反射变换)[10]。空间中的三维柱面的姿态都是随机的,将柱面的轴向利用豪斯霍尔德变换至与测量坐标系中的Z轴平行,就可以将柱面投影至XOY平面,利用点的X、Y坐标拟合曲线。最终表达一个柱面模型的参数分别是(α,β,a0,a1,a2…an),其中α、β分别是柱面轴向与X、Y轴的夹角,a0、a1、a2…an是二维曲线表达式的系数。
2 三维空间柱面拟合 2.1 计算法向量对于求解法向量的方法有很多,本文采用主成分分析法(principal component analysis,PCA),该方法利用搜索查询点的k(k ≥ 3)邻域构造协方差矩阵,协方差矩阵反映了该邻域局部曲面的变化规律,由此可以求解该矩阵特征值和特征向量来估计查询点的法向量。
查询点pi的协方差矩阵C为:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}} = \frac{1}{k}\sum\limits_{i = 1}^k {\left( {{p_i} - \bar p} \right)} \cdot {{\left( {\bar p - {p_i}} \right)}^{\rm{T}}}}\\ {\mathit{\boldsymbol{C}} \cdot \overline {{v_j}} = {\lambda _j} \cdot {{\bar v}_j}, j \in \{ 0, 1, 2\} } \end{array}} \right. $ | (2) |
式中,k是点pi领域点的数目;p表示所有领域点的重心坐标;λj是协方差矩阵的第j个特征值;vj是第j个特征向量。
利用雅克比方法求协方差矩阵C,其特征值为λ1、λ2、λ3(λ1 ≤ λ2 ≤ λ3),其对应的特征向量为n1、n2、n3。3个向量中最小特征值对应的特征向量n1就是查询点的法向量。为了方便,对于所有的法向量都标准化处理。
2.2 计算轴向向量利用柱面轴向与柱面点的法向量都垂直的特点求取柱面轴向向量l = (n,m,t),利用克拉默法则求取l,对于两个不共线上向量a = (x1,y1,z1),b = (x2,y2,z2)。
| $ \left[ {\begin{array}{*{20}{l}} {{x_1}}&{{y_1}}&{{z_1}}\\ {{x_2}}&{{y_2}}&{{z_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} n\\ m\\ t \end{array}} \right] = 0 $ | (3) |
| $ \left\{ {\begin{array}{*{20}{l}} {n = {y_1}{z_2} - {y_2}{z_1}}\\ {m = {x_2}{z_1} - {x_1}{z_2}}\\ {t = {x_1}{y_2} - {x_2}{y_1}} \end{array}} \right. $ | (4) |
首先判断a与b的夹角,由于点云数较大,保证轴向向量计算的可靠性,设置阈值θab,θab为a与b的夹角。
| $ \left[ {\begin{array}{*{20}{c}} {{l_1}}\\ {{l_2}}\\ \vdots \\ {{l_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{n_1}}&{{m_1}}&{{t_1}}\\ {{n_2}}&{{m_2}}&{{t_2}}\\ \vdots & \vdots & \vdots \\ {{n_i}}&{{m_i}}&{{t_i}} \end{array}} \right] $ | (5) |
取
将轴向向量
| $ R{(\bar n, \bar m, \bar t)^{\rm{T}}} = {(0, 0, 1)^{\rm{T}}} $ | (6) |
式中,R为旋转矩阵,由豪斯霍尔德变换求得R.
| $ \mathit{\boldsymbol{\omega }} = \frac{{\bar l - |\bar l|z}}{{|\bar l - |\bar l|z|}} $ | (7) |
| $ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{E}} - 2\mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}} $ | (8) |
| $ \mathit{\boldsymbol{R}} = {R_1}(\alpha ){R_2}(\beta ){R_3}(\gamma ) $ | (9) |
式中,E为单位矩阵;γ = 0,此时R 3(γ) = 1,
在得到旋转矩阵R后,将点云通过旋转调整至与x、y轴平面垂直的姿态。此时柱面物体在x、y轴平面的投影就是一条曲线。由点云的x,y坐标通过最小二乘求多项式系数就能把柱状物体的大小确定下来了。
| $ y = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + \cdots + {a_n}{x^n} $ | (10) |
本文采用Riegl VZ-1000对某建筑物倾斜圆柱体进行扫描,Riegl VZ-1000是脉冲式扫描,标称作业距离为1 400 m,单次扫描精度为5 mm/100 m,本次数据采集的距离小于100 m,故点云的精度在5 mm以内。在扫描得到的点云数据中裁剪出研究对象点云,利用统计分析技术剔除点云数据中的离群点,计算每个点到它所有邻域内点的平均距离,假设得到的结果是一个高斯分布,其形状由均值和标准差定义,平均距离在标准范围(有全局距离平均值和方差定义)之外的点,可被定义为离群点并剔除,最终采用体素格网化法进行下采样后点云如图 1所示,计算点云的法向量之后得到轴向量为(0. 418,0. 114,0. 485),经过豪斯霍尔德转换得到旋转矩阵R。
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{r}} { - 0.625}&{ - 0.443}&{0.643}\\ { - 0.443}&{0.879}&{0.175}\\ {0.643}&{0.175}&{0.746} \end{array}} \right] $ |
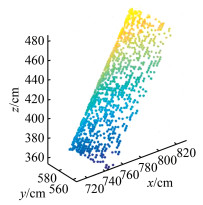 |
| 图 1 原始圆柱点云 Fig.1 Original Cylindrical Point Cloud |
通过坐标转换将倾斜圆柱点云数据转换值与xoy平面垂直如图 2所示,将点云数据投影至xoy平面,利用最小二乘算法求取圆的圆心和半径,得到圆的表达式为:(X + 456.828)2 +(Y - 214.149)2 = 29.8152,最终圆柱面拟合如图 3所示。
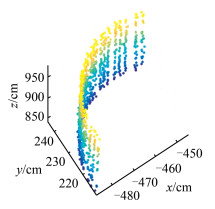 |
| 图 2 旋转后圆柱点云 Fig.2 Cylindrical Point Cloud After Rotation |
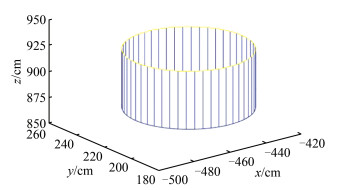 |
| 图 3 拟合圆柱面 Fig.3 Fitting a Cylindrical Surface |
对拟合后的圆柱面利用旋转矩阵进行姿态调整,旋转回初始姿态,利用初始点云数据与拟合后旋转柱面参数进行误差分析,计算每个点至圆柱面的距离,如图 4所示,除少部分噪声点影响,大部分的误差控制在0. 05 cm以内。
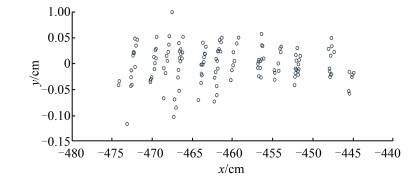 |
| 图 4 拟合残差 Fig.4 Fitting Residuals |
3.2 一般柱面拟合
本文采用Riegl VZ-1000对某大学行政楼扫描的部分数据进行验证,如图 5所示,部分点云数据如表 1所示(已经过重心化处理)。计算点云的法向量之后得到轴向量为(-0. 443,-0. 110,-0. 512),经过豪斯霍尔德转换得到旋转矩阵R。
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{r}} {0.761}&{ - 0.059}&{ - 0.646}\\ { - 0.059}&{0.985}&{ - 0.160}\\ { - 0.646}&{ - 0.160}&{ - 0.746} \end{array}} \right] $ |
 |
| 图 5 行政楼影像图 Fig.5 Image of the Administrative Building |
| 表 1 部分点云数据 Tab.1 Some Point Cloud Data |
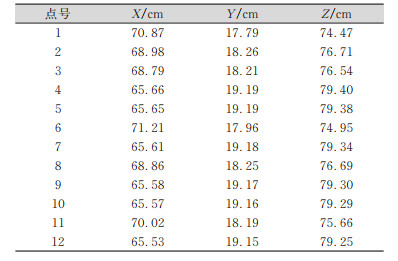 |
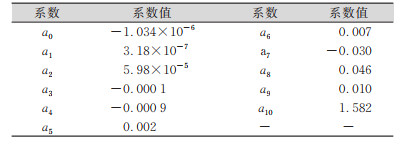
由此得到α =arccos0. 985=9. 93°,β =arc- cos0. 761=40. 45°。通过坐标转换以后利用X、Y坐标拟合曲线,采用5阶至10阶多项式对坐标转换后投影至xoy平面点云数据进行拟合,经过实验采用10阶多项式拟合效果最好,各项系数(见表 2)如下:a0=-1. 034×10-6,a1=3. 18×10-7,a2=5. 98×10-5,a3=-0. 000 1,a4=-0. 000 9,a5=0. 002,a6=0. 007,a7=-0. 03,a8=0. 046,a9=0. 01,a10=1. 582,旋转后点云如图 6所示,其中拟合的曲线如图 7所示。
| 表 2 多项式系数 Tab.2 Polynomial Coefficients |
 |
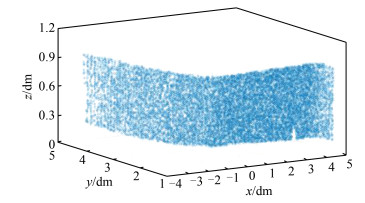 |
| 图 6 旋转后点云 Fig.6 Point Cloud After Rotation |
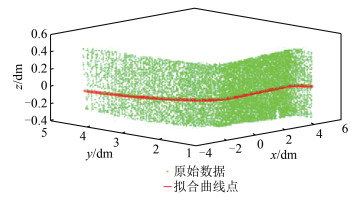 |
| 图 7 拟合曲线 Fig.7 Fitting Curve |
最终拟合的曲面如图 8所示。最后根据拟合点云到拟合曲面的距离评定拟合精度,空间距离投影到xoy平面上就是点到曲线的距离,最后得到的距离残差图如图 9所示,绝大部分点云偏离曲面都在0. 03 cm以内。拟合的精度满足一般的工程曲面拟合精度。
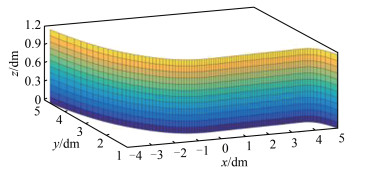 |
| 图 8 拟合曲面 Fig.8 Fitting Surface |
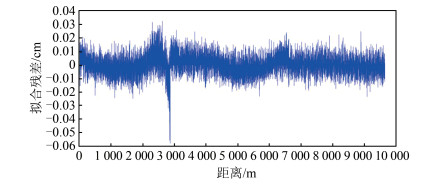 |
| 图 9 拟合残差 Fig.9 Fitting Residuals |
4 结束语
针对空间中任意姿态一般的柱面,提出了先计算其轴向向量,通过豪斯霍尔德变换进行投影,降维处理来达到拟合一般曲面的曲线公式,在从二维扩展到三维空间。并以实例进行验证,取得了较好的效果。在曲线拟合的时候对于不同的曲面需要综合考虑曲线的阶数,以达到最佳效果。
| [1] |
符华年, 刘兴虎, 李俊峰. 基于地面激光点云数据的NURBS曲面重建[J]. 测绘地理信息, 2017, 42(4): 17-19. |
| [2] |
姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报·信息科学版, 2012, 37(3): 4-7. |
| [3] |
潘国荣, 谷川. 改进的遗传算法用于工业测量数据处理[J]. 大地测量与地球动力学, 2008, 28(1): 59-62. |
| [4] |
谷川, 潘国荣, 施贵刚, 等. 基于遗传算法的曲面拟合参数辨识[J]. 武汉大学学报·信息科学版, 2009, 34(8): 983-986. |
| [5] |
张益泽, 王解先. 初值任意选取的圆柱面拟合方法[J]. 工程勘察, 2012(1): 80-83. |
| [6] |
田晓, 李全海. 基于坐标转换的三维空间圆柱面拟合[J]. 工程勘察, 2014(12): 79-82. |
| [7] |
王解先. 工业测量中一种二次曲面的拟合方法[J]. 武汉大学学报·信息科学版, 2007, 32(1): 50-53. |
| [8] |
王解先, 季凯敏. 工业测量拟合[M]. 北京: 测绘出版社, 2008.
|
| [9] |
丁克良, 刘全利, 陈翔. 正交距离圆曲线拟合方法[J]. 测绘科学, 2008, 33(S1): 72-73. |
| [10] |
Chen Junping, Wang Jiexian. The Conic Fitting in Engineering Surveying[J]. Geo-technical Investigation and Surveying, 2003(5): 59-61. |
 2022, Vol. 47
2022, Vol. 47
