| 捷联惯导在地铁轨道检测中的应用 |
传统静态轨道检测采用轨检小车和全站仪合作,布设CPIII控制网,对每个轨枕进行静态测量,计算轨道不平顺性。在地铁轨检中,受地铁运营和相关安全因素的影响,此方法存在效率不高、检测里程短等缺陷[1-3]。捷联惯导是利用陀螺仪和加速度计测量载体相对于惯性空间的角速度和线速度沿载体坐标系的分量,经过积分计算和坐标转换,得到载体的位置、速度、航向和水平姿态等各种导航信息,但是捷联惯导存在误差随时间积累的弊端。近年来,惯导已应用于高铁轨检的研究,采用INS(inertial navigation system)/GPS组合导航的方式,达到了比较好的精度,并且提高了作业效率。在地铁轨检实验中,以全站仪测量所得的坐标代替GPS测量坐标,建立组合导航模型,对惯导误差进行修正,计算轨道几何参数,与轨检小车检测所得的轨道不平顺性进行对比,分析惯导解算精度,为后续实验提供参考。
1 捷联惯性导航数字算法捷联惯导系统的关键技术包括初始对准问题、有害加速度的消除以及引力修正、捷联惯导误差模型的建立和实时补偿、捷联矩阵的更新等。在惯导解算过程中,首先建立相应误差模型,进行初始对准得到初始姿态角,在捷联矩阵更新算法的基础上,计算得到更新后的姿态方位角、载体运动速度以及位置[4]。
1.1 初始对准及解算模型粗对准时,轨检小车静止停放于轨道上,加速度计测量重力加速度g在载体坐标系(b系)中的分量gb,陀螺仪测量地球自转角速度ωie在载体坐标系中的分量ωieb。由于对准地点的地理位置为已知量,所以这两个量在导航坐标系(n系)中的分量gn和ωien也是已知的,并且为常值。载体系至导航系的姿态矩阵Cbn为[5]:
| $ {\bf{C}}_b^n = {\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\bf{g}}^n}} \right)}^{\rm{T}}}}\\ {{{\left( {\mathit{\boldsymbol{\omega }}_{\mathit{ie}}^\mathit{n}} \right)}^{\rm{T}}}}\\ {{{\left( {{{\bf{g}}^n} \times \mathit{\boldsymbol{\omega }}_{\mathit{ie}}^\mathit{n}} \right)}^{\rm{T}}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\bf{g}}^b}} \right)}^{\rm{T}}}}\\ {{{\left( {\mathit{\boldsymbol{\omega }}_{\mathit{ie}}^\mathit{b}} \right)}^{\rm{T}}}}\\ {{{\left( {{{\bf{g}}^n} \times \mathit{\boldsymbol{\omega }}_{\mathit{ie}}^\mathit{b}} \right)}^{\rm{T}}}} \end{array}} \right] $ | (1) |
粗对准求得的姿态矩阵因存在误差,不满足单位正交条件,精对准之前还应当进行单位正交化。
精对准一般采用卡尔曼滤波方法建立包含3个失准角的状态方程和量测方程,状态方程和量测方程根据捷联惯导系统误差方程建立相应模型。捷联惯导系统误差方程如下[6]。
1) 姿态误差方程为:
| $ \mathit{\boldsymbol{\dot \varphi }} = - \mathit{\boldsymbol{\omega }}_{\mathit{in}}^\mathit{n} \times \mathit{\boldsymbol{\varphi }}{\rm{ + }}\delta \mathit{\boldsymbol{\omega }}_{\mathit{in}}^\mathit{n}{\rm{ - }}\delta \mathit{\boldsymbol{\omega }}_{\mathit{ib}}^\mathit{n} $ | (2) |
式中,φ为姿态角矩阵;ωinn=ωien+ωenn,其中,ωien=[0, ωiecosL, ωiesinL]T,ωie为地球自转角速率;
2) 速度误差方程为:
| $ \begin{array}{l} \delta \mathit{\boldsymbol{\dot v}} = {\mathit{\boldsymbol{f}}^n} \times \mathit{\boldsymbol{\varphi }}-\left( {2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en}^n} \right) \times \delta {\mathit{\boldsymbol{v}}^n} + \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{v}}^n} \times \left( {2\delta \mathit{\boldsymbol{\omega }}_{ie}^n + \delta \mathit{\boldsymbol{\omega }}_{en}^n} \right) + \delta {\mathit{\boldsymbol{f}}^n} \end{array} $ | (3) |
式中,vn为速度矩阵;fn为捷联惯导测量所得比力矢量。
3) 位置误差方程为:
| $ \left\{ \begin{array}{l} {\rm{ \mathit{ δ} }}\dot L = \frac{{\delta v_N^n}}{{{R_M} + h}}-\frac{{v_N^n}}{{{{({R_M} + h)}^2}}}\delta h\\ {\rm{ \mathit{ δ} }}\dot \lambda = \frac{{{\rm{sec}}L}}{{{R_N} + h}}\delta v_E^n + \frac{{{\rm{sec}}L{\rm{tan}}L}}{{{R_N} + h}}v_E^n\delta L-\frac{{v_E^n{\rm{sec}}L}}{{{{({R_N} + h)}^2}}}\delta h\\ {\rm{ \mathit{ δ} }}\dot h = \delta v_U^n \end{array} \right. $ | (4) |
式中,L、λ、h分别为纬度、精度、高程;vNn、vEn、vUn分别为导航坐标系下北向、东西、天顶方向速度;RM、RN分别为子午圈曲率、卯酉圈曲率半径。
假设捷联惯导经过严格标定以后陀螺和加速度计标定误差均很小,可以忽略其影响,并假设陀螺漂移误差为随机常值漂移,加速度计偏置误差为随机常值偏置。定义如下15维状态向量[6, 7]:
| $ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}}&{\begin{array}{*{20}{c}} {\mathit{\delta }{{\left( {{\mathit{\boldsymbol{v}}^n}} \right)}^{\rm{T}}}}&{\mathit{\delta }{\mathit{\boldsymbol{p}}^{\rm{T}}}} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{\varepsilon }}^b}} \right)}^{\rm{T}}}}&{{{\left( {{\nabla ^b}} \right)}^{\rm{T}}}} \end{array}} \end{array}} \right]^{\rm{T}}} $ | (5) |
可得到卡尔曼滤波精对准状态方程为:
| $ \mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{F}}_{{\rm{INS}}}}\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{W}} $ | (6) |
式中,
| $ {\mathit{\boldsymbol{F}}_{{\rm{INS}}}} = \left[ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} { - (\mathit{\boldsymbol{\omega }}_{in}^n \times )}&{{\mathit{\boldsymbol{F}}_{12}}}&{{\mathit{\boldsymbol{F}}_{13}}}&{ - \mathit{\boldsymbol{C}}_b^n}&{{{\bf{0}}_{{\rm{3}} \times {\rm{3}}}}}\\ {\left( {{\mathit{\boldsymbol{f}}^n} \times } \right)}&{{\mathit{\boldsymbol{F}}_{{\rm{22}}}}}&{{\mathit{\boldsymbol{F}}_{23}}}&{{{\bf{0}}_{3 \times 3}}}&{\mathit{\boldsymbol{C}}_b^n}\\ {{{\bf{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{\mathit{\boldsymbol{F}}_{{\rm{32}}}}}&{{\mathit{\boldsymbol{F}}_{{\rm{33}}}}}&{{{\bf{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\bf{0}}_{{\rm{3}} \times {\rm{3}}}}} \end{array}}\\ {\begin{array}{*{20}{c}} {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\bf{0}}_{6 \times 15}}} \end{array}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{F}}_{12}} = \left[{\begin{array}{*{20}{c}} 0&{-\frac{1}{{{R_M} + h}}}&0\\ {\frac{1}{{{R_N} + h}}}&0&0\\ {\frac{{{\rm{tan}}L}}{{{R_N} + h}}}&0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{F}}_{{\rm{22}}}} = ({\mathit{\boldsymbol{v}}^\mathit{n}} \times ){\mathit{\boldsymbol{F}}_{12}}-\left( {\left( {2\mathit{\boldsymbol{\omega }}_{\mathit{ie}}^\mathit{n} + \mathit{\boldsymbol{\omega }}_{\mathit{en}}^\mathit{n}} \right) \times } \right) $ |
| ${\mathit{\boldsymbol{F}}_{32}} = \left[{\begin{array}{*{20}{c}} 0&{\frac{1}{{{R_M} + h}}}&0\\ {\frac{{{\rm{sec}}L}}{{{R_N} + h}}}&0&0\\ 0&0&1 \end{array}} \right]$ |
| $ {\mathit{\boldsymbol{F}}_{13}} = \left[{\begin{array}{*{20}{c}} 0&0&{\frac{{\mathit{\boldsymbol{v}}_N^n}}{{{{({R_M} + h)}^2}}}}\\ {-{\omega _{ie}}{\rm{sin}}L}&0&{-\frac{{\mathit{\boldsymbol{v}}_E^n}}{{{{({R_N} + h)}^2}}}}\\ {{\omega _{ie}}{\rm{cos}}L}&0&{-\frac{{\mathit{\boldsymbol{v}}_E^n{\rm{tan}}L}}{{{{({R_N} + h)}^2}}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{F}}_{23}} = ({\boldsymbol{v}^\mathit{n}} \times )\left[{\begin{array}{*{20}{c}} 0&0&{\frac{{v_N^n}}{{{{({R_M} + h)}^2}}}}\\ {-2{\omega _{ie}}{\rm{sin}}L}&0&{-\frac{{v_E^n}}{{{{({R_N} + h)}^2}}}}\\ {2{\omega _{ie}}{\rm{cos}}L}&0&{-\frac{{v_E^n{\rm{tan}}L}}{{{{({R_N} + h)}^2}}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{F}}_{33}} = \left[{\begin{array}{*{20}{c}} 0&0&{-\frac{{v_N^n}}{{{{({R_M} + h)}^2}}}}\\ {\frac{{v_E^n{\rm{sec}}L}}{{{R_N} + h}}{\rm{tan}}L}&0&{-\frac{{v_E^n{\rm{sec}}L}}{{{{({R_M} + h)}^2}}}}\\ 0&0&0 \end{array}} \right] $ |
取捷联惯导系统的速度误差作为观测量。在静基座条件下,捷联惯导系统的速度输出即为速度误差,因天顶方向速度变化很小,在计算时可忽略天顶方向速度的影响,所以量测方程为:
| $ \mathit{z}{\rm{ = }}\mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{V}} $ | (7) |
式中, z=[δvE δvN]T;
姿态更新算法对保证捷联惯导算法精度起了决定性的影响,速度算法其次,位置算法贡献最小。捷联惯导简化算法推导的特点是:对于慢变物理量不使用递推式,而是以在tm-1时刻的近似值代替其在tm-1≤t≤tm时间段的平均值。捷联惯导简化算法微分方程组可写为如下形式[7, 8]。
1) 姿态更新四元微分方程为:
| $ \mathit{\boldsymbol{\dot q}}_\mathit{b}^\mathit{n} = \frac{{\rm{1}}}{{\rm{2}}}\mathit{\boldsymbol{q}}_\mathit{b}^\mathit{n}\mathit{\boldsymbol{\omega }}_{\mathit{nb}}^\mathit{b} $ | (8) |
式中,ωnbb=ωibb-(Cbn)Tωinn, 其中,ωibb为角速度矩阵; qbn为四元数, 可与捷联姿态矩阵Cbn以及姿态角φ互相转换。
2) 速度更新微分方程为:
| $ {\mathit{\boldsymbol{\dot v}}^\mathit{n}} = {\mathit{\boldsymbol{f}}^\mathit{n}}-\left( {2\mathit{\boldsymbol{\omega }}_{\mathit{ie}}^\mathit{n} + \mathit{\boldsymbol{\omega }}_{\mathit{en}}^\mathit{n}} \right) \times {\mathit{\boldsymbol{v}}^\mathit{n}} + {\mathit{\boldsymbol{g}}^\mathit{n}} $ | (9) |
式中,fn=Cbngb;gn=[0 0-g]T,g为当地加速度数值。
3) 位置更新微分方程为:
| $ \left\{ \begin{array}{l} \dot L = \frac{{v_N^n}}{{{R_M} + h}}\\ \dot \lambda = \frac{{{\rm{sec}}L}}{{{R_N} + h}}v_E^n\\ \dot h = v_U^n \end{array} \right. $ | (10) |
在实验过程中,采用测量机器人对轨检小车进行跟踪测量,得到小车运动过程中的坐标以及里程信息。组合导航系统设计可以借鉴INS/GPS组合导航的方式,以全站仪测量得到的坐标代替GPS坐标,建立组合导航模型[8-12]。
对式(7)进行相关修改。修改后为z=[zvT zpT]T,
实验位于武汉地铁2号线某段,所选区域为直线段,实验过程中,小车前进方向为小里程方向,解算过程中忽略了臂杆效应产生的影响。采用NV-INS600惯性导航系统,将惯导设备固定在轨检小车上。采样频率设置为200 Hz。惯导坐标系采用东北天坐标系,载体坐标系为右前上坐标系。
首先采用轨检小车,每隔一个轨枕进行静态轨道检测,为保证精度,进行往返测,并记录数据。然后采用惯导采集数据,静态观测了约7 min,同时采用MS50测量机器人观测轨检小车棱镜,获取初始位置里程、中线坐标。初始对准完成后,推动轨检小车前进,进行动态数据采集,MS50测量机器人同时进行跟踪观测,并记录观测数据。
数据处理过程中,首先将加速度数据变化成增量形式,初始对准采用静态测量前5 min采集的数据解算,动态测量过程选取了约40 s的数据进行解算。以静态观测时全站仪测量所得的中线坐标、高程作为惯导解算初始数据,得到了各采样点姿态角、运动速度以及位置信息,进而计算得到实测轨道中线坐标、里程、高程、轨道超高等参数。在得到里程信息后,根据设计文件,可得到对应里程处的设计中线坐标以及高程信息。整理轨检小车和捷联惯导解算所测量得到的轨道平顺性参数,并结合设计文件进行数据分析。
2.2 实验成果经过初始对准,可得到惯导解算的初始姿态角与轨检小车测量所得的姿态角以及设计方位角、坡度、倾角。各项数据整理如表 1所示。
| 表 1 初始对准成果/rad Table 1 Initial Alignment Results /rad |
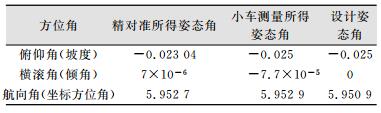 |
由表 1可知,由轨检小车测量得到的坡度、倾角以及坐标方位角比较接近设计值,由惯导解算得到的俯仰角与航向角相对设计值的相对误差分别为7.84%、0.16%,捷联惯导算法误差应当控制在整个捷联系统误差的5%以内[9]。横滚角为小角度,结果均接近设计值。航向角偏离较大,可以建立大失准角模型对航向角加以修正。
经组合导航更新后,可得到各采样点处小车的姿态角,由全站仪测量得到小车初始位置轨道实测中线坐标以及高程,结合惯导更新姿态,计算得到小车里程、对应里程处中线坐标以及高程,由横滚角和轨距测量得到超高。将惯导解算姿态变化成果与轨检小车测量所得成果进行对比,如图 1所示。
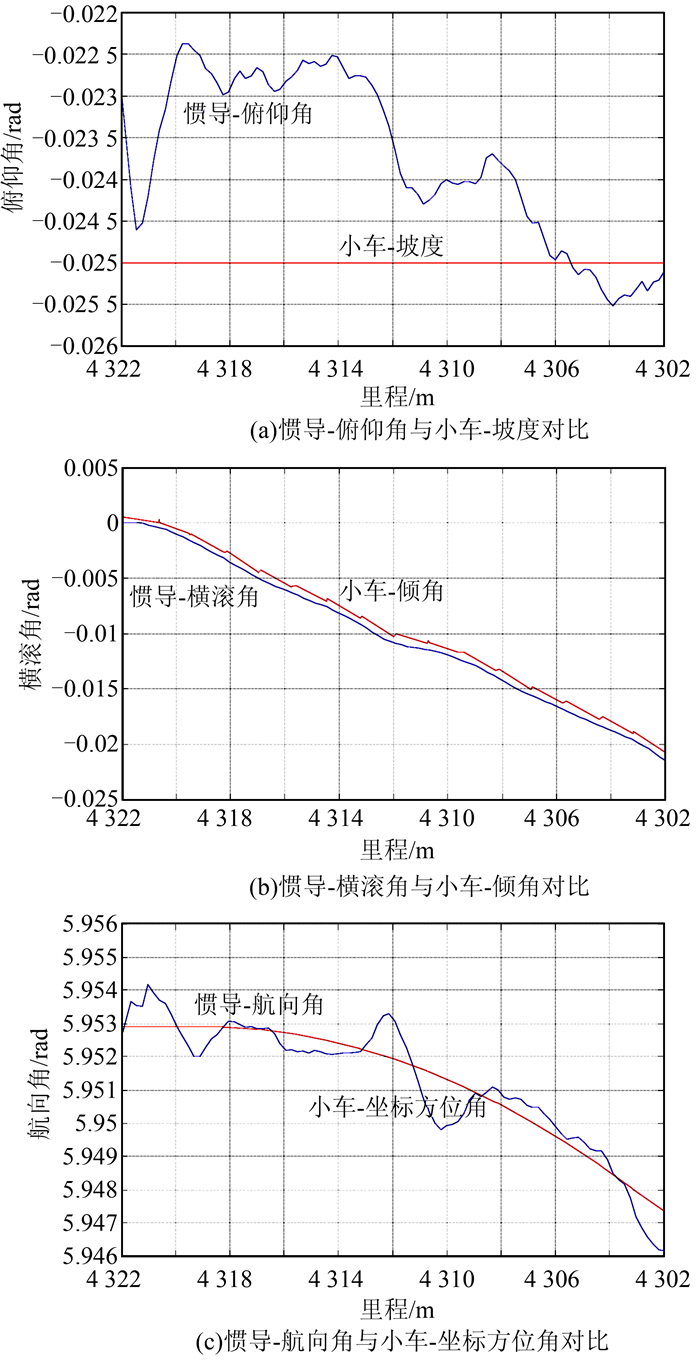 |
| 图 1 解算结果对比图 Figure 1 Comparison of Computed Results |
实验过程没有惯导设备与小车之间的安装误差以及臂杆效应等引起的系统误差,因此,惯导解算姿态角与小车测量值之间存在系统性偏差。
分析图 1可知,俯仰角解算虽然波动较大,但是波动幅度较小,并且在小车测量所得坡度附近变化;横滚角变化趋势与小车测量值趋势相同,有较好的符合性;航向角的变化也基本上在小车测量值附近波动,变化趋势与小车测量得到的坐标方位角基本上一致。
根据惯导更新姿态以及初始位置坐标、高程信息解算地铁轨道平顺性参数,将成果与经过轨检小车检测得到的平顺性参数进行对比,选取前22 m左右数据进行分析,结果如图 2所示。
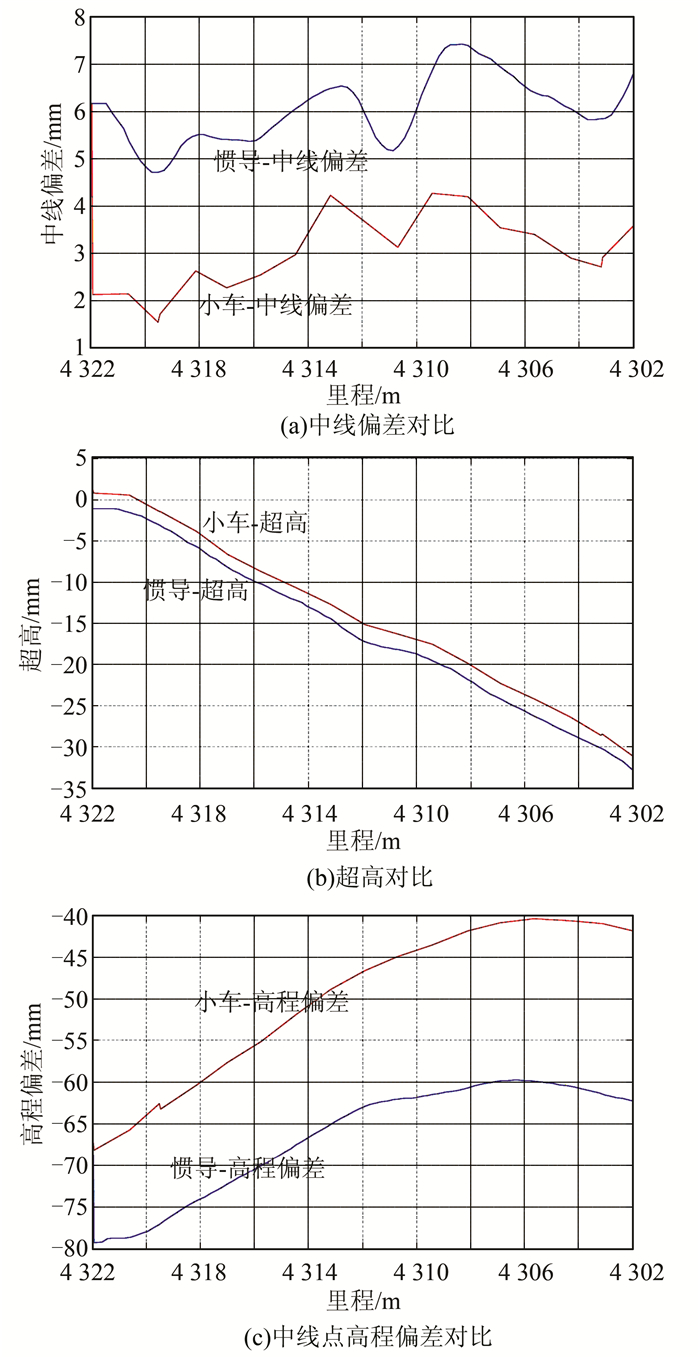 |
| 图 2 分析对比图 Figure 2 Comparison of Analysis Results |
分析图 2可知,经过惯导数据解算得到的轨道超高和轨面高程与轨检小车检测得到的中线偏差、超高、轨面高程变化趋势大致相同,表明组合导航对惯导误差发散有较好的抑制作用,惯导计算轨道不平顺性与传统测量方式有较好的符合性,惯导可以为小车提供比较准确的姿态信息,进而提高轨检的效率。
3 结束语经过组合导航解算之后,姿态角能较好地反映轨道变化的真实情况,该方法便捷快速,可以提高工作效率,并且可以为小车以及小车加载的其他测量设备提供姿态信息。
在后续实验过程中,还有很多工作需进一步研究,如建立模型或标定计算得到惯导误差安装角等引起的系统误差;利用里程计,结合地铁隧道CPIII控制网以及全站仪约束惯导误差,建立INS/DR组合导航模型;通过实验验证ZUPT(zero velocity update)算法对提高解算精度的作用等。
| [1] |
董志国. 铁轨检测小车的机构设计与测量算法[D]. 太原: 太原理工大学, 2006 |
| [2] |
娄继冰. 铁路轨道参数检测及其数据处理技术的研究[D]. 长沙: 中南大学, 2007 |
| [3] |
钟昊然. 轨道几何状态测量仪检测方法研究[D]. 成都: 西南交通大学, 2013 |
| [4] | 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998 |
| [5] |
杨艳芳. 捷联惯性导航系统关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2001 |
| [6] | 万德钧, 房建成. 惯性导航初始对准[M]. 南京: 东南大学出版社, 1998 |
| [7] | Shin E H. Estimation Techniques for Low-Cost Inertial Navigation[D]. Calgary: The University of Calgary, 2005 |
| [8] |
严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006 |
| [9] | Savage P G. Strapdown Inertial Navigation Integration Algorithm Design (Part 1):Attitude Algorithms[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(1): 19–28 DOI: 10.2514/2.4228 |
| [10] | 郭际明, 李昕, 张鹏. 基于固定点初始化的室内伪卫星定位方法研究[J]. 测绘地理信息, 2017, 42(2): 1–4 |
| [11] | 车通宇, 杨力, 张传定. SDP4模型用于北斗宇航卫星轨道预报的精度分析[J]. 测绘地理信息, 2017, 42(2): 12–16 |
| [12] | 邹进贵, 马佑, 肖扬宣. 对流层延迟模型对GPS高程时间序列的影响分析[J]. 测绘地理信息, 2016, 41(5): 8–11 |
 2018, Vol. 43
2018, Vol. 43


