| 北斗卫星钟差频间偏差及对定位精度影响分析 |
2. 地球空间信息技术协同创新中心,湖北 武汉,430079;
3. 武汉大学灾害监测和防治研究中心,湖北 武汉,430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China;
3. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China
随着GNSS的发展,现代化之后的GPS、BDS等已经开始三频信号的发射,其中北斗是目前唯一全星座提供三频信号的卫星导航系统[2]。研究表明,使用三频信号可以提高定位精度、加快模糊度解算,但由于北斗卫星三频载波相位观测值中存在明显的不一致性,导致利用B1/B2观测值生成的精密卫星钟差产品并不适用于基于B1/B3观测值的精密单点定位(precise point positioning, PPP),即采用不同频率组合观测的卫星钟差间存在一定差异[1]。由于这种不一致性最终会引入到卫星钟差中,因而这种不一致性称作卫星钟差频间偏差(inter-frequency clock bias, IFCB)。
Montenbruck等[3, 4]提出采用最小二乘,多次模拟计算得到卫星钟差频间偏差(IFCB)和模糊度的大概解。Hauschild等[5]对日本QZSS卫星系统的IFCB进行了特性分析,发现其具有系统性和周期性。最小二乘可以估计求得IFCB,但是比较费时并且因为要计算模糊度所以算法比较复杂,对此,李浩军等[1]提出了历元间差分(epoch-differenced, ED)及历元和卫星双差(satellite-and epoch-differenced, SDED)模型。另外,还有太阳-地球-卫星模型[6]和高阶谐波函数模型[7],它们是根据地球的运动规律提出的经验模型。本文利用全球分布的5个测站连续两周的观测数据对北斗地球静止轨道(GEO)卫星和倾斜地球同步轨道(IGSO)卫星以及中地球轨道(MEO)卫星中的IFCB进行了特性分析[8],并将前一天数据计算得到的IFCB改正值用于第二天基于B1/B3的北斗精密单点定位,比较了其定位精度的变化情况。考虑到低高度角的观测噪声比较大,本文通过降权来减弱其影响。
1 卫星钟差频间偏差估计方法卫星s和测站r间的三频相位观测方程为[9]:
| $\begin{matrix} {L_r^s(K) = \rho + T + c{\text{d}}{t_r} + ( - c{{\text{dt}}^s} + {b^s}) -} \\ { {I_1} \cdot f_1^2/f_K^2 + {\text{const}} = \rho + T + c{\text{d}}{t_r} - c\overline {{\text{d}}{t^s}} - } \\ {{I_1} \cdot f_1^2/f_K^2 + {\text{const}}} \\ \end{matrix} $ | (1) |
式中,ρ是站星距; T是对流层延迟; cdtr是接收机钟差; 而cdts是卫星钟差,能和卫星误差bs一起归为
在频率i和j之间的电离层自由组合测量为:
| $ \begin{gathered} {\text{IF}}({B_i}, {B_j}) = \frac{{f_j^2}}{{f_j^2 - f_i^2}} \cdot {B_j} - \frac{{f_i^2}}{{f_j^2 - f_i^2}} \cdot {B_i} \\ = \rho + T + c{\text{d}}{t_r} - c\overline {{\text{d}}{t^s}} (i, j) + {{\text{const}}_{if}} \\ \end{gathered} $ | (2) |
式中, Bi为相应i频率的相位观测值; B1、B2和B3频率上的观测值可以组成不同的消电离层组合; B1/B2和B1/B3消电离层相位组合观测值作差,可以消除几何距离和对流层延迟参数,只剩下模糊度项和卫星钟差频间偏差。差分的消电离层组合(differenced ionosphere-free, DIF)观测值为[3-4]:
| $\begin{matrix} {{\text{DIF}}({B_1}, {B_2}, {B_3}) = {\text{IF}}({B_1}, {B_2}) - {\text{IF}}({B_1}, {B_3}) =} \\ {{\text{IFCB}} + {{\text{const}}_{1, 2}} - {{\text{const}}_{1, 3}}} \\ \end{matrix} $ | (3) |
| $ {\text{IFCB}} = - c\overline {{\text{d}} {t^s}} (1, 2) + c\overline {{\text{d}}{t^s}} (1, 3) $ | (4) |
式中,const1, 2和const1, 3分别表示B1/B2和B1/B3消电离层组合观测值中的模糊度项;
根据式(3)、式(4),参照卫星钟差产品的生成过程,即可估计得到IFCB[3, 10]。
| $ \text{IFCB}=\text{DIF}({{B}_{1}}, {{B}_{2}}, {{B}_{3}})-\text{cons}{{\text{t}}_{1, 2}}+\text{cons}{{\text{t}}_{1, 3}} $ | (5) |
假设相邻两个历元没有周跳发生,那么历元间作差就可以把式(5)中的模糊度项消除[2]。对于相邻两个历元m和m-1,差分公式如下:
| $ \Delta \text{IFCB}(m)=\text{DIF}({{B}_{1}}, {{B}_{2}}, {{B}_{3}})(m)-\text{DIF}({{B}_{1}}, {{B}_{2}}, {{B}_{3}})(m-1) $ | (6) |
式中,“Δ”表示历元间差分操作; ΔIFCB是历元间差分的IFCB。
IFCB与时间和卫星相关[2],而后面实验发现,IFCB与测站位置不相关,理论上对于所有测站ΔIFCB(m)均应相等,但实际因为观测噪声的存在有所差异,不同测站解算的结果不完全一致。为了提高解的可靠性,降低不可靠性观测带来的影响,一方面可以增加参考网中测站数量求平均;另外可以采取加权的方法,根据实验研究,当高度角低于40°时,观测噪声开始明显增大,为了削弱低高度角观测值噪声的影响,对其ΔIFCB值进行降权。其权的形式如下:
| $ w=\left\{ \begin{align} &\sin E\ \ E<{{40}^{\circ }} \\ &\ \ 1\ \ \ \ E\ge {{40}^{\circ }} \\ \end{align} \right. $ | (7) |
式中,E是卫星的高度角; w是各测站ΔIFCB对应的权值。
假设参考网中有n个测站,对各测站得到的ΔIFCB(m)(k=1~n)加权取平均,即可得:
| $ \Delta \text{IFCB}(m)={\sum\limits_{k=1}^{n}{(\Delta \text{IFCB}{{(m)}_{k}}}\cdot {{w}_{k}})}/{\sum\limits_{k=1}^{n}{{{w}_{k}}}}\; $ | (8) |
假设第一个历元的IFCB为零,那么第m个历元的IFCB可以表示如下:
| $ \text{IFCB}(m)=\sum\limits_{t=2}^{m}{\Delta \text{IFCB}(t)} $ | (9) |
为解决第一个历元IFCB值不确定这个问题,由IFCB的周期性和随机性两个特性,引入了一个限制条件,即IFCB所有历元都添加一个系统常数,以使得一个周期内所有历元的IFCB之和为零。假设一周期内有p个历元,那么第m个历元最终的IFCB可以按如下求得:
| $ \overline{\text{IFCB}}(m)=\text{IFCB}(m)-{\left( \sum\limits_{\text{t=1}}^{\text{p}}{\text{IFCB(t)}} \right)}/{p}\; $ | (10) |
由此获得的IFCB可能所有历元均含有一个常数偏差,不同周期该常数偏差可能还存在一定差值。在PPP浮点解中,该偏差会被模糊度参数吸收,并不受影响;但在PPP固定解中,会影响整周模糊度的固定。
2 IFCB数据计算及对定位精度影响分析 2.1 IFCB与测站位置相关性分析为了考察IFCB与测站位置的相关性,同时考虑目前北斗的覆盖区域仍限于亚太地区,为观测到尽可能多的北斗卫星,本次实验从全球MGEX(Multi-GNSS Experiment)测站选取5个在2015年11月1日的数据进行分析。测站分布信息如图 1所示,且均装有“Trimble NetR9”型GNSS接收机,可以提供北斗B1、B2、B3三频数据,观测数据的采样间隔是30 s,截止高度角设为10°。
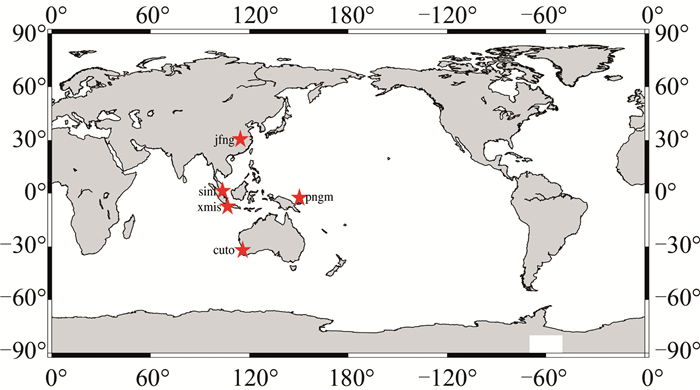 |
| 图 1 所选5个测站的位置 Fig.1 Location of Five Stations |
进行相关性分析前,首先需对观测数据进行预处理[11],并使用三频观测值进行周跳探测与修复[12],继而通过对卫星连续观测历元的DIF求平均近似得到模糊度项,由各历元DIF减去DIF平均值后,即可粗略得到IFCB[4]。但是上述方法只能获得相对的DIF,并且各测站对同一颗卫星跟踪时间长短不一致,导致不同测站相同卫星同一历元的IFCB不同。为了便于对比分析,在各卫星连续观测历元弧段的IFCB中均加入了一个常数偏差,使得不同测站相同卫星相同历元的IFCB差异最小。求取图 1中5个测站各卫星的IFCB,除去北斗系统中未使用的试验卫星和失控卫星,总共考虑13颗卫星,结果如图 2所示。
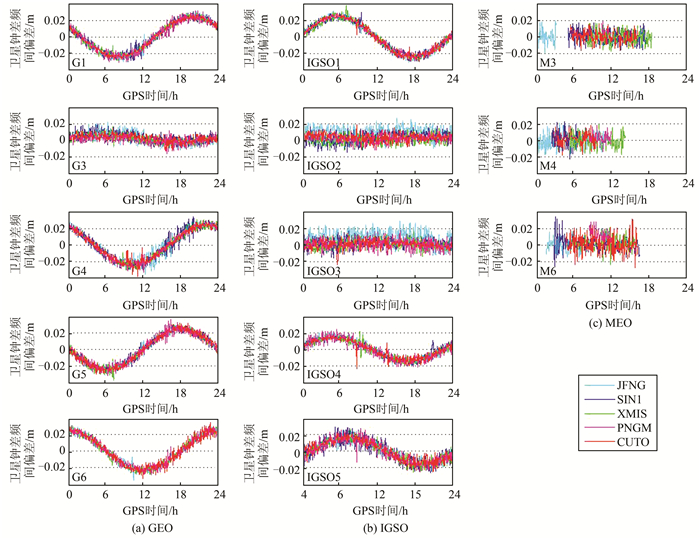 |
| 图 2 2015年11月1日5个测站各北斗卫星的IFCB Fig.2 BeiDou Satellites IFCB of Five Stations on the 1th November 2015 |
从图 2中可以看出,除了G3、IGSO2、IGSO3卫星外,不同测站GEO和IGSO卫星的IFCB变化趋势一致,表明这些卫星的IFCB高度相关。而其他卫星相关性较低,特别是MEO卫星,表现为随机噪声特性,解算的IFCB值断断续续不具有连续性且没有明显的周期性,可能是由于其IFCB趋势项并不明显,而噪声误差占优造成的。而噪声和高度角密切相关,对同一个测站而言,在卫星运行的一个周期内不同时段高度角不同,另外测站纬度越高,观测同一颗卫星为低高度角的时间相对越长,这体现在图 2中误差项有一定的时间性,由G3、IGSO2、IGSO3卫星的结果可以看出,5个测站中JFNG和CUTO测站噪声影响最大。
综上分析可知,IFCB与时间和卫星相关,而与测站位置本身无关,为了削弱低高度角带来的影响,可以采取降权处理,从而证明本文的方法是可行的。
2.2 IFCB数值估计与特性分析利用本文提出的加权历元间差分方法对IFCB进行数值估计,实验采用2015年11月1日~14日数据,因为MEO卫星计算得到的IFCB都不具有连续性及周期性,故不考虑,得到剩余10颗北斗卫星的IFCB,如图 3所示。
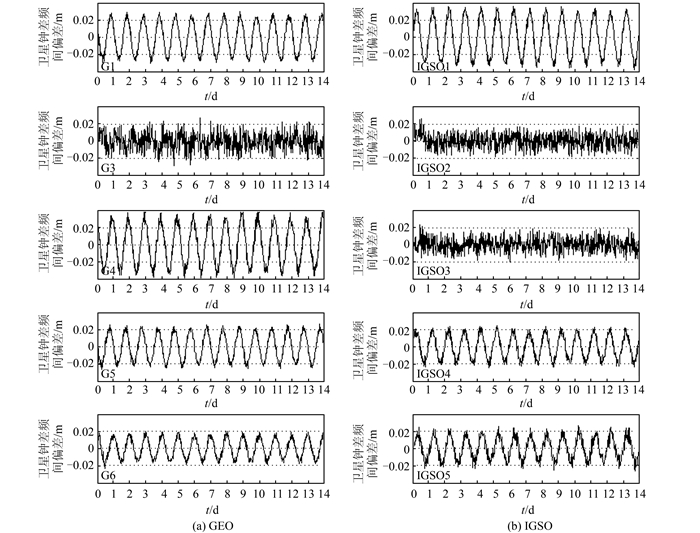 |
| 图 3 2015年11月1日~14日各北斗卫星的IFCB Fig.3 IFCB of the Compass Satellites from November 1 to 14, 2015 |
从图 3中可以看出,加常数调整后的IFCB都在-4~4 cm之间变化。从图 3还可以看出大部分GEO和IGSO卫星IFCB呈明显的周期性变化,而G3、IGSO2及IGSO3的结果周期性不明显,需要进一步测试分析。
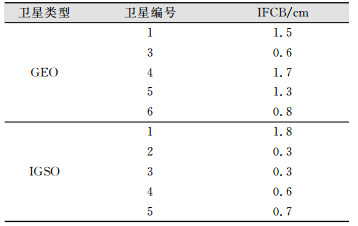
为了进行定量分析,统计了图 3中GEO和IGSO卫星IFCB的RMS值,结果如表 1所示。从表中可知,所有卫星IFCB的RMS值均小于2 cm。其中,IGSO2与IGSO3卫星IFCB最小,其RMS值约为0.3 cm;而G1、G4、G5与IGSO1卫星IFCB较大,其RMS值均大于1.3 cm。
| 表 1 2015年11月1日~14日各北斗卫星IFCB的RMS统计值 Tab.1 RMS Statistics of IFCB of the Compass Satellites from November 1 to 14, 2015 |
 |
2.3 IFCB对定位精度影响分析
考虑到IFCB具有良好的周期性,如图为24 h左右,因而可以利用前一天数据计算得到的IFCB,对第二天观测数据进行改正,从而提高定位精度。为了测试IFCB对定位性能的改善情况,采用以下3种策略进行北斗PPP:
策略1 使用B1/B3载波相位观测值;
策略2 使用B1/B3载波相位观测值,利用前一天数据计算得到的IFCB对G1、G4、G5、G6、IGSO1、IGSO4、IGSO5观测值进行改正,其他卫星观测值降权处理;
策略3 使用B1/B2载波相位观测值。
为了排除伪距中偏差的影响,北斗PPP并没有使用伪距观测值。为了解决接收机钟差与模糊度参数秩亏的问题,将伪距单点定位计算得到的接收机钟差作为先验约束。依此计算了每组数据最后15 min定位误差的RMS值,然后求其平均值进行,统计结果如表 2所示。
| 表 2 3种策略北斗精密单点定位误差/cm Tab.2 Three Kinds of Strategy BeiDou Precision Single Point Positioning Error/cm |
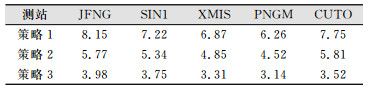 |
由表 2可以看出,不同频率组合适用于不同的应用场合,相较于B1/B3而言,明显B1/B2双频组合定位误差低更适用于精密单点定位;采用B1/B3消电离层组合观测值进行IFCB改正后,5个测站的定位精度比改正前有1.74 cm~2.38 cm的提高,但和直接基于B1/B2观测值的PPP相比,定位精度较低,表明仍然有部分IFCB没有改正。
3 结束语本文总结了Montenbruck和李浩军等的理论模型[1, 3],针对低高度角观测噪声的影响,在历元间差分基础上提出一种加权的方法并对其进行了验证。实验先是考察IFCB与测站位置的相关性,继而利用5个测站连续14 d的观测数据对GEO卫星和IGSO卫星IFCB特性进行分析。其结果显示:
1) IFCB与时间和卫星有关,与测站无关;
2) 部分GEO卫星、IGSO卫星IFCB具有明显的周期性,其相邻两天的IFCB高度相关;
3) 相应卫星IFCB振幅在4 cm以内变动,其均方根误差(RMS)小于2 cm;
4) 将前一天数据计算得到的IFCB值用于第二天基于B1/B3观测值的北斗精密单点定位,虽然不及直接使用B1/B2的单点定位精度,但定位精度有显著改善,为用三频相位改正钟差偏差提供了基础。
| [1] |
Li Haojun, Zhou Xuhua, Wu Bin, et al. Estimation of the Inter-Frequency Clock Bias for the Satellites of PRN25 and PRN01[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(11): 2 186-2 193. DOI:10.1007/s11433-012-4897-0 |
| [2] |
杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1 734-1 740. |
| [3] |
Montenbruck O, Hugentobler U, Dach R, et al. Apparent Clock Variations of the Block IIF-1 (SVN62) GPS Satellite[J]. GPS Solutions, 2012, 16(3): 303-313. DOI:10.1007/s10291-011-0232-x |
| [4] |
Montenbruck O, Hauschild A, Steigenberger P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211-222. DOI:10.1007/s10291-012-0272-x |
| [5] |
Hauschild A, Steigenberger P, Rodriguez-Solano C. Signal, Orbit and Attitude Analysis of Japan's First QZSS Satellite Michibiki[J]. GPS Solutions, 2012, 16(1): 127-133. DOI:10.1007/s10291-011-0245-5 |
| [6] |
Li Haojun, Zhou Xuhua, Wu Bin. Fast Estimation and Analysis of the Inter-Frequency Clock Bias for Block IIF Satellites[J]. GPS Solutions, 2013, 17(3): 347-355. DOI:10.1007/s10291-012-0283-7 |
| [7] |
Li Haojun, Chen Yanling, Wu Bin, et al. Modeling and Initial Assessment of the Inter-Frequency Clock Bias for COMPASS GEO Satellites[J]. Advances in Space Research, 2013, 51(12): 2 277-2 284. DOI:10.1016/j.asr.2013.02.012 |
| [8] |
付宁波, 陈艳梅, 黄霞飞. 基于GPS跟踪站的精密单点定位精度分析[J]. 测绘地理信息, 2015, 40(4): 29-31. |
| [9] |
冯来平.GPS多频观测数据处理方法及应用研究[D].郑州: 信息工程大学, 2009 http://cdmd.cnki.com.cn/Article/CDMD-90008-1011270730.htm
|
| [10] |
Montenbruck O, Steigenberger P, Schnemann E, et al. Flight Characterization of New Generation GNSS Satellite Clocks[J]. Navigation, 2012, 59(4): 291-302. DOI:10.1002/navi.v59.4 |
| [11] |
李盼, 郭斐, 刘季. 实时精密单点定位中的数据预处理研究[J]. 测绘地理信息, 2012, 37(5): 29-32. |
| [12] |
Zhao Qile, Sun Binzi, Dai Zhiqiang, et al. Real-Time Detection and Repair of Cycle Slips in Triple-Frequency GNSS Measurements[J]. GPS Solutions, 2015, 19(3): 381-391. DOI:10.1007/s10291-014-0396-2 |
 2019, Vol. 44
2019, Vol. 44


