| 大型构件平面度和直线度快速测量方法 |
平面度是用来表示物体(通常指刚体)的实测平面要素与设计的理想平面的状态,也可以称作物体的平整程度。直线度是指连接测量值的起点和终点得到一条直线,将相距该直线偏移的最大差值作为直线度,用来评定物体的准直程度[1-3]。整体平面度与整体直线度指的是物体在拼接过程中对于平面度和直线度的整体控制情况,用最小二乘和统计学中的样本方差来定量表示。
所睿等[4]利用双频激光干涉仪进行直线度测量,用于精密机床、大规模集成电路加工设备等的直线度误差修正;刘鹏[5]研究了激光准直系统进行铁路长导轨直线度测量;柴光远等[6]研究了利用间隙法、光轴法、平晶干涉法在零件的加工中的平面度量度。上述研究主要集中在精密仪器以及零件的加工,对于大型构件拼接的平面度和直线度监测不太适用,且这些测量系统的结构复杂,成本高。大型刚体结构拼接过程中的直线度与平面度的快速监测以及拼接完成后的状态量监测问题,是大型精密工程测量技术需要解决的,而这方面研究较少。
1 3种测量模型为了保证大型刚体构件和铁路轨道等大型精密工程运行时符合设计要求,需要对其平面度和直线度等关键状态量进行测量。拼接之前要先确定拼接的方向,在合适的位置放置用于定向的标志,将其设定为0°方向角。在其拼接过程中,需要对布设的监测点进行测量。
1.1 基于一、二维测量的状态量测量一维、二维测量,指的是测量角度、距离或者高程等其中的一个或两个元素信息。基于一维、二维测量来完成直线度和平面度的状态量的监测思路如下:以整个刚体的分部件为例,在其表面布设8个监测点,如图 1所示,用水准仪分别测量1~6号点的高一维、二维测量,指的是测量角度、距离或者高程等其中的一个或两个元素信息。基于一维、二维测量来完成直线度和平面度的状态量的监测思路如下:以整个刚体的分部件为例,在其表面布设8个监测点,如图 1所示,用水准仪分别测量1~6号点的高
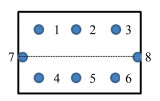 |
| 图 1 模型1分部件监测点图 Fig.1 Model 1 Component Monitoring Point Diagram |
1)平面度。已知分部件的理论设计高程,监测点的高程和分部件的理论设计高程的高程起算基准点相同,可以得到的各个监测点的高程hi。监测点到理论设计高程平面的最大高程差f1,即为分部件的平面度。参考最小二乘和统计学样本方差[7, 8],g1可以评价整个刚体结构的整体平整度情况。
| $ \left\{\begin{array}{l} f_{1}=h_{\max }-h_{\min } \\ g_{1}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(h_{i}-\tilde{h}\right)^{2}}{n}} \end{array}\right. $ | (1) |
2)直线度。利用用于直线度计算的监测点到基准站的距离以及相对于设计中轴直线的方位角,可以计算得到各个监测点到设计中轴线的垂距dj,其中最大的值dmax(f1') 即为该刚体的直线度,各监测点到中轴线的垂距的样本方差g1'来评价整体直线度情况。
| $ \left\{\begin{array}{l} d_{j}=s_{j} \cdot \sin \alpha_{j} \\ f_{1}^{\prime}=d_{\max } \\ g_{1}^{\prime}=\sqrt{\frac{\sum\limits_{j=1}^{m} d_{j}^{2}}{m}} \end{array}\right. $ | (2) |
三维测量,通常指的是一次性获取目标点在某个空间坐标系下的三维坐标信息(X,Y,Z)。基于三维测量来完成直线度和平面度的状态量的监测思路如下:以整个刚体的分部件为例,在其表面布设4个监测点,如图 2所示,将构件拼接的方向设置为0°方位角,用全站仪或激光跟踪仪测量1~4号点的三维坐标。
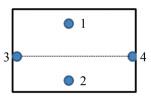 |
| 图 2 模型2分部件监测点图 Fig.2 Model2Component Monitoring Point Diagram |
1)平面度。空间中3个不共线的已知点可以确定一个平面,空间平面的方程可以表示为ax + by + cz + d = 0,将采集到的4个监测点,通过间接平差求得平面的系数可以得到一个拟合平面。根据空间点到空间平面的距离公式,可以得到监测点(xi,yi,zi)到平面的距离di,规定在拟合平面之上的用dmax+表示,在拟合平面之下的用dmax-表示。监测点到拟合平面两侧的最大距离的和,即为分部件的平面度f2。各监测点到拟合平面的样本方差g2,可以评价整个刚体结构的整体平整度情况。
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {a{x_1} + b{y_1} + c{z_1} + d = 0}\\ {a{x_2} + b{y_2} + c{z_2} + d = 0}\\ {a{x_3} + b{y_3} + c{z_3} + d = 0}\\ {a{x_4} + b{y_4} + c{z_4} + d = 0} \end{array}}& \to \end{array}} \right.\\ \mathit{v}{\rm{ = }}\mathit{aX}{\rm{ + }}\mathit{bY}{\rm{ + }}\mathit{cZ}{\rm{ + }}\mathit{d} \end{array} $ | (3) |
| $ \left\{\begin{array}{l} f_{2}=d_{\max }^{+}+d_{\max }^{-} \\ g_{2}=\sqrt{\frac{\sum\limits_{i=1}^{m} d_{i}^{2}}{n}} \end{array}\right. $ | (4) |
2)直线度。将监测点投影到拟合的平面上,求出位于分部件中轴线两端的监测点的中间点坐标,利用拟合算法对位于中轴线上的监测点以及求得的中间点进行直线拟合,投影到平面后z=Z,可以得到形如y = k1x + k0的拟合直线。监测点到拟合直线的最大距离dmax即为该刚体的直线度f2',监测点到拟合直线的样本方差g2'来评价整体直线度情况。
| $ \left\{\begin{array}{l} k_{1}=\frac{\sum\limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum\limits_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \\ k_{0}=\bar{y}-k_{1} \bar{x} \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} f_{2}^{\prime}=d_{\max } \\ g_{2}^{\prime}=\sqrt{\frac{\sum\limits_{j=1}^{m} d_{j}^{2}}{m}} \end{array}\right. $ | (6) |
六自由度指一个物体在三维空间中最多有6个自由度,即3个位置参数信息(X,Y,Z),3个姿态角信息(α,β,γ)。对于正前方的一个刚体,可以利用其方位角α来反映其直线度,利用它的俯仰角β和横滚角γ来反映其平面度。传统的六自由度测量是通过测量一个刚体上不同在一条直线上的3个及以上的目标点的三维坐标,进而反算出刚体相对于测站的姿态信息。这种方法适用于静止状态下的状态量监测,且效率较低,对于准静态或者动态物体的状态量监测无法快速反馈出姿态信息。为了快速获得物体的六自由度信息,考虑基于全站仪的单目标六自由度测量,如图 3所示,只需在刚体的中心位置布设一个观测点即可得到该刚体相对于基准站的六自由度信息。通过将反射棱镜进行改造和集成,让到达反射棱镜的大部分光原路返回用于测量坐标,一小部分光透过棱镜进入到后面的CCD图像传感器,根据入射光在CCD图像传感器上的成像位置,可以获得偏航角和俯仰角的信息,再加装一个倾角传感器得到自身相对水平面的倾角可以得到目标物体相对于基准站的横滚角。经高扬等[9]的实验验证,该集成系统可以提供0. 01°水平的姿态测量精度。
 |
| 图 3 模型3分部件监测点图 Fig.3 Model 3 Component Monitoring Point Diagram |
1)平面度。各个分部件的设计长度e和宽度w是已知的,基于全站仪的单目标六自由度测量系统得到各监测点的三维坐标(xi,yi,zi),计算得到各监测点相对于基准站的距离l。对于已经拼接完成的分部件,l可以验证它相当于基准站的位置是否发生变化,对于正在拼接的分部件,可以计算其移动速度,及时做出调整。将测量得到的俯仰角β和横滚角γ代入式(7)可以直接得到各分部件的平面度以及评定整个刚体结构的整体平整度情况。
| $ \left\{\begin{array}{l} l=\sqrt{\left(x_{i}^{2}+y_{i}^{2}+z_{i}^{2}\right)} \\ d_{i}=\frac{w}{2} \sin \beta_{i}+\frac{e}{2} \sin r_{i} \\ f_{3}=d_{\max }^{+}+d_{\max }^{-} \\ g_{3}=\sqrt{\frac{\sum\limits_{i=1}^{m} d_{i}{ }^{2}}{n}} \end{array}\right. $ | (7) |
2) 直线度。将测量得到的各监测点相对于设计的拼接方向的方位角
| $ \left\{\begin{array}{l} d_{i}^{\prime}=\frac{w}{2} \sin \alpha_{i} \\ f_{3}^{\prime}=d_{\max }^{\prime} \\ g_{3}^{\prime}=\sqrt{\frac{\sum\limits_{i=1}^{m} d_{i}{ }^{2}}{n}} \end{array}\right. $ | (8) |
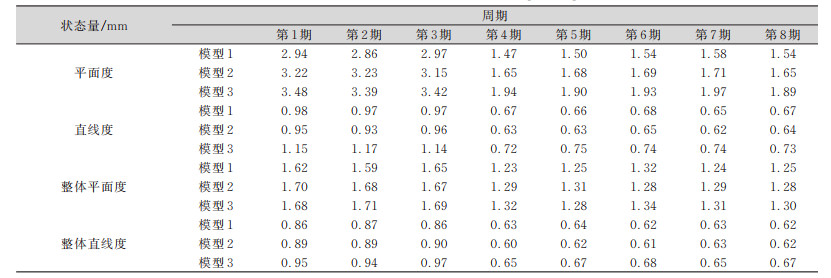
本文选取模拟大型刚体构件拼接安装的测量数据,该构件有十几个分部件组成,每个分部件的长度约8. 2 m,宽度约2. 0 m。要求调整结束后构件的平面度控制在3 mm以内,直线度要求控制在1 mm以内。表 1给出了按照本文提出的3种模型的数据拟合后得到的结果。
| 表 1 3种模型8期的状态量 Tab.1 State Value of Three Models in Eight Stage |
 |
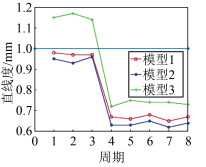
利用Matlab程序分析3种监测模型的状态量数据,绘于图 4、图 5中。从两图中可以明显看出状态量在第3期到第4期发生了显著的变化,是因为在首次拼接完成后测量了3期,发现监测的状态量都在限定值的周围浮动,为了确保工程的质量,所以进行了整体的调整。
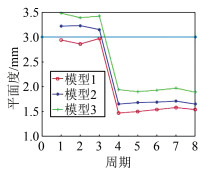 |
| 图 4 平面度结果 Fig.4 Planarity Results |
 |
| 图 5 直线度结果 Fig.5 Stanghtness Results |
从图 4中可以看出,在不考虑数据获取时间的前提下,模型1是通过直接获得的数据拟合得到的,因此模型1得到的平面度数据更具说服力。由图 4得到3种测量模型的监测值相当且数据稳定,因此也可以得到模型2与模型3是可靠的。由图 5可以得到,在不考虑数据获取时间和动态拼接的前提下,模型1与模型2的测量效果更好,但模型3的测量结果同样也可以满足要求。
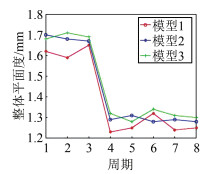
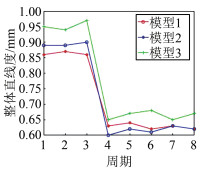
整体平面度和整体直线度可以反映出物体在拼接过程中对于平面度和直线度的整体控制情况。如图 6、图 7所示。
 |
| 图 6 整体平面度结果 Fig.6 Global Flatness Results |
 |
| 图 7 整体直线度结果 Fig.7 Global Straightness Results |
从图 6可以看出拼接刚体的整体平面度数据与图 4中刚体的平面度数据基本呈正相关。在进行整体调整之前,拼接刚体的整体直线度都小于1. 8 mm,而直线度数据(除模型1)大于3 mm,产生这种结果的原因可能是,在拼接过程中某些分部件的平面度控制不够理想。同理,由图 7和图 5对比,可以看出拼接刚体的整体直线度数据与刚体的直线度数据也基本呈正相关。3种模型下刚体的整体直线度均小于1 mm,但模型3的前3期直线度大于1 mm,造成此结果的原因可能是某些分部件的直线度数据过大。因此,在评价最终的拼接质量时,可以把整体直线度和整体平面度的数据当作一个参考指标,并根据相关要求严格控制直线度和平面度这两个状态量。
面对已经拼接完成的静态及准静态刚体的平面度和直线度监测,3种测量模型都可以选用,模型3更方便快捷;但是对于刚体的动态监测安装,想要快速准确的完成拼接任务,采用模型3更为合适。但是模型3也有其局限性,当拼接的分部件过大时,无法满足上面的精度限制要求。
3 结束语针对大型精密工程拼接安装过程的平面度和直线度测量问题,本文给出了3种测量模型。并将六自由度测量技术应用于快速状态测量,给出了监测的模型以及数据的处理与评价方法。通过本文探讨表明六自由度测量技术应用于大型设备的分部件拼接监测具有更好的适用条件,可以快速完成静态和动态的平面度及直线度两个状态量的测量,为六自由度测量技术的在大型精密工程测量应用提供了一个新思路。
| [1] |
李广云, 范百兴. 精密工程测量技术及其发展[J]. 测绘学报, 2017, 46(10): 1742-1751. DOI:10.11947/j.AGCS.2017.20170313 |
| [2] |
李亚军, 郑志刚. 直线度误差的数据处理及程序设计[J]. 中国测试技术, 2007(3): 67-69. |
| [3] |
黄富贵. 平面度误差各种评定方法的比较[J]. 工具技术, 2007, 41(8): 107-109. DOI:10.3969/j.issn.1000-7008.2007.08.033 |
| [4] |
所睿, 范志军, 李岩, 等. 双频激光干涉仪技术现状与发展[J]. 激光与红外, 2004, 34(4): 251-253. DOI:10.3969/j.issn.1001-5078.2004.04.003 |
| [5] |
刘鹏. 铁路长导轨直线度测量方法研究[D]. 西安: 中国科学院研究生院(西安光学精密机械研究所), 2009
|
| [6] |
柴光远, 周炯, 田满洲. 平面度误差检测方法的研究[J]. 机床与液压, 2007(5): 184-185. DOI:10.3969/j.issn.1001-3881.2007.05.065 |
| [7] |
鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报·信息科学版, 2008, 33(5): 504-507. |
| [8] |
丁克良, 沈云中, 欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(1): 44-47. DOI:10.3969/j.issn.1008-0562.2010.01.012 |
| [9] |
高扬. 面向大型精密工程的六自由度测量技术研究[D]. 天津: 天津大学, 2017
|
| [10] |
郭辉, 徐良骥. 导线网间接平差算法分析与实现[J]. 测绘科学, 2014, 39(3): 107-110. |
| [11] |
唐旭, 王平, 胡石元, 等. 基于需求载荷均衡的城市供水管网管径诊断方法[J]. 测绘地理信息, 2019, 44(2): 7-15. |
 2022, Vol. 47
2022, Vol. 47

