建立科学的教学质量评价体系是促进教学活动管理科学化、保证和提高教学质量、培养高素质合格人才的重要措施。现有的教学质量评价体系主要部分是评价指标和评价模型，评价指标是由反应教学过程中直接或间接影响教学质量和效果的重要因素有机构成，评价模型则是综合多因素对教学效果做出最佳评估的决策方法或数学模型^[1]。常用的教学评价体系多以学生评教为主，评价模型也是单一的加权求和法。该教学质量评价体系存在两个主要问题：一是虽然各项指标都有各自的分值，但大都是按一定比例固定进行分配，并不能准确地反映各指标间的权重关系以及这些指标对评价结果的不同影响。第二是教学评价的主体单一，多是以学生评教为主，学生的主观性将直接关系到评价结果的好坏，在一定程度上导致教学质量评价的偏面性。针对上述问题，许多学者已经做了大量的相关研究，由于教学质量各评价指标之间以及与评价结果间是一种复杂非线性关系，而人工神经网络具有非线性、实时优化、智能学习等优点，成为当前教学质量评价的主要算法^[2-5]。本文是在上述研究基础上提出了结合主成分分析(principal component analysis, PCA)的BP神经网络模型的教学质量评价方法，主要解决现有BP神经网络教学质量评价模型中针对多维评教体系(学生评教、督导评教等)采用多个BP神经网络模型实现，不能体现多维评教体系的内在关联性问题。本文方法首先利用PCA分析多维评教体系，在减少其相关性，保留综合信息基础上，采用一个整体的BP神经网络模型处理多维评教问题。

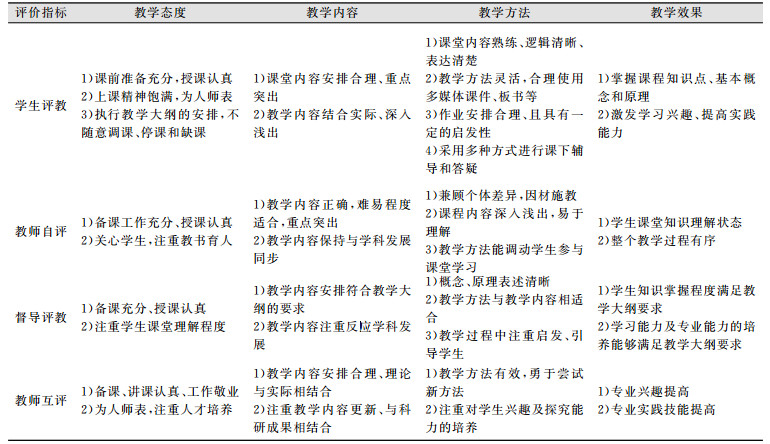
全面、合理、可行的教学质量评价指标是教学质量评价的基础，指标体系的构建应考虑评价主体的多元化、教学过程的规律及教学的根本目标等方面。根据多年的教学工作经验及参考现有相关文献的基础上, 尤其是借鉴参考文献[4]及参考文献[6]对我国和美国部分高校教学评价指标的对比分析，本文提出的教学质量评价指标体系见表 1。该评价指标由两级指标构成，第一级为教学态度、教学内容、教学方法及教学效果，第二级分别从学生评教、督导评教、教师自评及教师互评方面细化的评价指标。第二级指标是建立在第一级指标基础上的，具体细化过程为：(1)教学态度主要从教师备课、讲课认真负责及教师育人态度等方面细化指标。(2)教学内容主要从教学内容安排的合理性、前沿性及与实践相结合等方面细化指标。(3)教学方法主要从教学方法适宜性及对学生能力(自学能力、探究能力等)的潜在培养方面细化指标。(4)教学效果主要从学生知识掌握程度、学习能力、实践及创新能力等方面细化指标。同时，本文的教学质量评价指标体系也兼顾了参与者(学生和课程教师)及同行(督导和其他教师)的角度，多方位对教学过程和效果进行评估。

表 1(Tab.1)

表 1 教学质量评价指标体系 Tab.1 Teaching Quality Evaluation Index System

表 1 教学质量评价指标体系 Tab.1 Teaching Quality Evaluation Index System 评价指标 教学态度 教学内容 教学方法 教学效果 学生评教 1)课前准备充分，授课认真 2)上课精神饱满，为人师表 3)执行教学大纲的安排，不随意调课、停课和缺课 1)课堂内容安排合理、重点突出 2)教学内容结合实际、深入浅出 1)课堂内容熟练、逻辑清晰、表达清楚 2)教学方法灵活，合理使用多媒体课件、板书等 3)作业安排合理、且具有一定的启发性 4)采用多种方式进行课下辅导和答疑 1)掌握课程知识点、基本概念和原理 2)激发学习兴趣、提高实践能力 教师自评 1)备课工作充分、授课认真 2)关心学生，注重教书育人 1)教学内容正确，难易程度适合，重点突出 2)教学内容保持与学科发展同步 1)兼顾个体差异，因材施教 2)课程内容深入浅出，易于理解 3)教学方法能调动学生参与课堂学习 1)学生课堂知识理解状态 2)整个教学过程有序 督导评教 1)备课充分、授课认真 2)注重学生课堂理解程度 1)教学内容安排符合教学大纲的要求 2)教学内容注重反应学科发展 1)概念、原理表述清晰 2)教学方法与教学内容相适合 3)教学过程中注重启发、引导学生 1)学生知识掌握程度满足教学大纲要求 2)学习能力及专业能力的培养能够满足教学大纲要求 教师互评 1)备课、讲课认真、工作敬业 2)为人师表，注重人才培养 1)教学内容安排合理、理论与实际相结合 2)注重教学内容更新、与科研成果相结合 1)教学方法有效，勇于尝试新方法 2)注重对学生兴趣及探究能力的培养 1)专业兴趣提高 2)专业实践技能提高

PCA是一种基于统计特征的多维正交线性变换^[7]，常用来对数据进行特征提取和降维，主要原理是将分散在一组变量上的信息集中到某几个综合变量上，且得到的综合变量互不相关。

本文将多维评教指标体系作为一个整体运用于后续的BP神经网络评价模型，由于学生评教、督导评教、教师自评及教师互评4类指标均是对教学态度、教学内容、教学方法及教学效果的细化，因此存在一定相关性。PCA算法将用来对这些具有一定相关性的指标进行重新组合，根据特征值累计贡献率形成一组新的彼此之间互不相关的综合性指标，用这组新的指标来代替原来的指标进行后续分析。

反向传播网络(back-propagation network，BP网络)是一种按误差逆传播算法训练的多层前馈网络，由输入层、隐层和输出层组成^[8]。BP算法由信号的正向传播和误差的反向传播两个过程组成^{[9, 10]}。

对于教学质量评价而言，BP神经网络通过反向传播误差来修正模型权值这一特性，可以用来解决评价指标之间的权值问题，避免了传统评价体系中人为给定权值，提高评估结果的可靠性。教学质量评价BP模型的实现过程主要包括网络模型建立、网络模型设置、网络模型训练、测试与分析等步骤。可以将教学评价体系中的指标作为神经元输入，将评价的最终结果作为输出，建立评估模型。网络模型设置包括网络层数、每层中的神经元数和传递函数。在网络模型训练开始之前，需要给定网络模型参数如期望误差最小值、最大循环次数、修正权值的学习速率等，训练过程中当输出的量值和预期的量值满足误差要求，模型完成训练，得到确定的权值和阈值。测试与分析则是利用训练好的神经网络对测试数据做出正确评价。

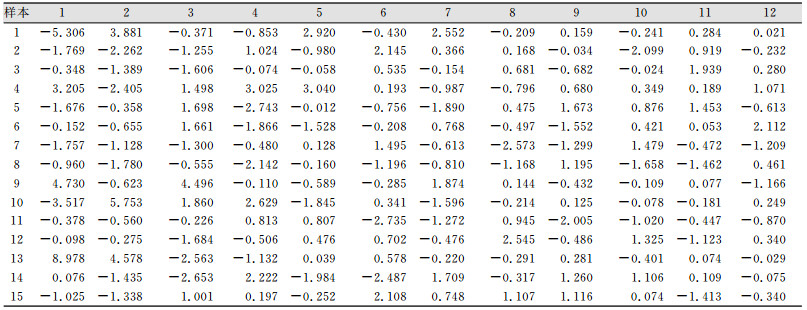
本文的实验是基于MATLAB搭建的BP神经网络模型下进行的，BP神经网络参数的设置为训练次数为3 000次，最小误差为0.000 1，学习率为0.01。PCA算法综合指标维数确定是取特征值累计贡献率达到0.99时的特征值个数。实验一共采集了15个样本的评教数据，进行了归一化处理，14个用来训练模型，1个用来测试。经过PCA变换后，保留前12项，如表 2所示。前14个样本数据进行BP网络模型训练，结果如图 1所示。图中横轴为样本数；纵轴为样本值。图 1(a)表明当训练次数18次时，网络误差已满足要求。图 1(b)中，+表示初始网络输出模型，“ -”代表的是训练后网络的输出波形。样本15作为测试数据，预测的结果是0.909 68，与实际评估值0.91非常接近，验证了本文方法的可行性。

表 2(Tab.2)

表 2 PCA变换后的样本数据 Tab.2 Sample Data after PCA Transformation

表 2 PCA变换后的样本数据 Tab.2 Sample Data after PCA Transformation 样本 1 2 3 4 5 6 7 8 9 10 11 12 1 -5.306 3.881 -0.371 -0.853 2.920 -0.430 2.552 -0.209 0.159 -0.241 0.284 0.021 2 -1.769 -2.262 -1.255 1.024 -0.980 2.145 0.366 0.168 -0.034 -2.099 0.919 -0.232 3 -0.348 -1.389 -1.606 -0.074 -0.058 0.535 -0.154 0.681 -0.682 -0.024 1.939 0.280 4 3.205 -2.405 1.498 3.025 3.040 0.193 -0.987 -0.796 0.680 0.349 0.189 1.071 5 -1.676 -0.358 1.698 -2.743 -0.012 -0.756 -1.890 0.475 1.673 0.876 1.453 -0.613 6 -0.152 -0.655 1.661 -1.866 -1.528 -0.208 0.768 -0.497 -1.552 0.421 0.053 2.112 7 -1.757 -1.128 -1.300 -0.480 0.128 1.495 -0.613 -2.573 -1.299 1.479 -0.472 -1.209 8 -0.960 -1.780 -0.555 -2.142 -0.160 -1.196 -0.810 -1.168 1.195 -1.658 -1.462 0.461 9 4.730 -0.623 4.496 -0.110 -0.589 -0.285 1.874 0.144 -0.432 -0.109 0.077 -1.166 10 -3.517 5.753 1.860 2.629 -1.845 0.341 -1.596 -0.214 0.125 -0.078 -0.181 0.249 11 -0.378 -0.560 -0.226 0.813 0.807 -2.735 -1.272 0.945 -2.005 -1.020 -0.447 -0.870 12 -0.098 -0.275 -1.684 -0.506 0.476 0.702 -0.476 2.545 -0.486 1.325 -1.123 0.340 13 8.978 4.578 -2.563 -1.132 0.039 0.578 -0.220 -0.291 0.281 -0.401 0.074 -0.029 14 0.076 -1.435 -2.653 2.222 -1.984 -2.487 1.709 -0.317 1.260 1.106 0.109 -0.075 15 -1.025 -1.338 1.001 0.197 -0.252 2.108 0.748 1.107 1.116 0.074 -1.413 -0.340

图 1(Fig.1)

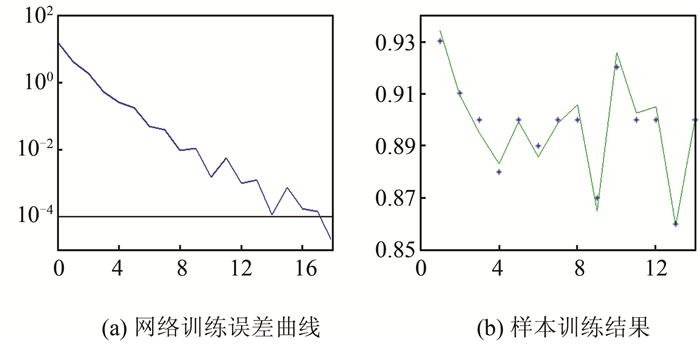图 1 BP网络模型训练 Fig.1 BP Network Training

本文将引入神经网络模型用于构建教学质量评价模型，利用其前向反馈计算和误差后向传播的特性，经过自适应学习获取评价指标之间的权值和评价结果输出阈值，解决传统评价方法的复杂建模问题，避免人为的主观随意度，保证评估结果的有效性。同时，利用主成分分析PCA对多维角度教学质量评价指标进行了降维，确保了多维评价指标作为整体进行BP模型训练和测试。本研究基于神经网络模型具有自主学习及从数据中挖掘规律的特点，旨在建立一个科学合理的教师教学质量评价模型，为教学质量评估的研究发展提供有益的参考。