| 基于星光角距的月球探测器地月转移轨道天文导航研究 |
月球是距离人类最近的星体,是开展深空探测的首选目标。而且月球具有可供人类开发和利用的独特资源,这些资源是对地球资源的重要补充和储备。我国于2013-12-02发射了嫦娥三号卫星,首次实现了月球软着陆和月面巡视勘察。嫦娥五号卫星也即将发射。这些探测活动对月球探测器的位置信息提出了更高的精度要求。
天文导航是指通过观测天体来确定探测器位置和速度的导航方法。它具有自主能力强、不受时空限制、不依赖于地面且不受大气影响的优点,是一种重要的自主导航方法,在国内外各个领域得到了广泛应用[1-5]。深空探测中由于飞行距离过远可能产生难以接受地面站信息的问题,天文导航可以克服这一问题。
我国也加紧了深空探测的步伐,李小军等[6]提出利用太阳高度角和方位角进行天文导航的方法,但是仅适用于月面探测器;刘建栋[7]提出了利用脉冲星进行天文导航的方法,但是该方法在z轴的精度相对x轴和y轴较差。因此,本文将对利用星光角距观测值对月球探测器导航的观测方程、状态方程和扩展卡尔曼滤波模型的建立,以及地月转移轨道段月球探测器的导航实验进行研究。
1 解算模型推导基于星光角距观测值的月球探测器天文导航方法通过对星光角距观测值进行计算,得到月球探测器的位置以及速度信息。通过星敏感器识别星光,通过地球敏感器得到探测器与地球的关系,将这两部分信息转化到探测器本体坐标系中,得到每个时刻的星光角距观测值,星光角距观测值的含义如图 1所示。
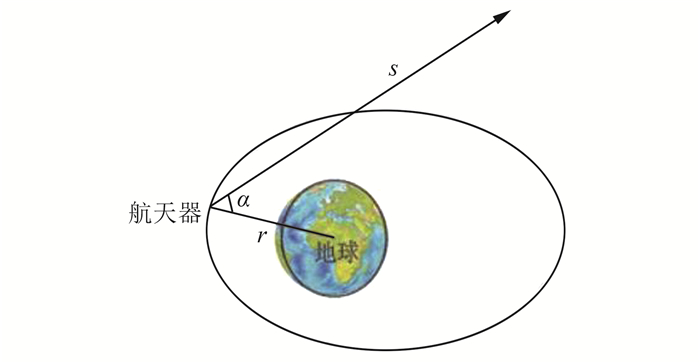 |
| 图 1 星光角距观测值含义 Fig.1 Observation of Starlight Angular |
1.1 观测方程
星光角距观测值的观测方程为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\alpha _1}{\rm{ = }}\arccos \left( {{\mathit{\boldsymbol{r}}_e}{\rm{ \times }}{\mathit{\boldsymbol{s}}_1}} \right) + {v_{{\alpha _1}}}}\\ {{\alpha _2}{\rm{ = }}\arccos \left( {{\mathit{\boldsymbol{r}}_e}{\rm{ \times }}{\mathit{\boldsymbol{s}}_2}} \right) + {v_{{\alpha _2}}}}\\ {{\alpha _3}{\rm{ = }}\arccos \left( {{\mathit{\boldsymbol{r}}_e}{\rm{ \times }}{\mathit{\boldsymbol{s}}_3}} \right) + {v_{{\alpha _3}}}} \end{array}} \right. $ | (1) |
式中,α1、α2、α3分别为星光角距观测值;re为月球探测器对地球方向的矢量;s1、s2、s3分别为月球探测器对星光方向的矢量;vα1、vα2、vα3为量测噪声。
令Zt=[α1, α2, α3]T,V=[vα1, vα2, vα3]T,则观测方程的矩阵形式为:
| $ {\mathit{\boldsymbol{Z}}_t} = \mathit{\boldsymbol{H}}(X(t)) + \mathit{\boldsymbol{V}} $ | (2) |
式中, X(t)表示月球探测器的状态参数;H(X(t))表示观测量与状态参数的函数关系。
1.2 状态方程选用月球探测器的状态模型考虑地球中心引力、J2项引力以及月球中心引力,则轨道动力学方程[8, 9]为:
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}\mathit{\boldsymbol{x}}}}{{{\rm{d}}t}} = {\mathit{\boldsymbol{v}}_x} + {\omega _x}, \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = {\mathit{\boldsymbol{v}}_y} + {\omega _y}, \frac{{{\rm{d}}\mathit{\boldsymbol{z}}}}{{{\rm{d}}t}} = {\mathit{\boldsymbol{v}}_z} + {\omega _z}\\ \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}} = - {\mu _e}\frac{\mathit{\boldsymbol{x}}}{{{r^3}}}\left[ {1 - {J_2}(\frac{{{R_e}}}{r})(7.5\frac{{{\mathit{\boldsymbol{z}}^2}}}{{{r^2}}} - 1.5)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mu _m}(\frac{{\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_m}}}{{r_{sm}^3}} + \frac{{{\mathit{\boldsymbol{x}}_m}}}{{r_m^3}}) + {\omega _{{v_x}}}\\ \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_y}}}{{{\rm{d}}t}} = - {\mu _e}\frac{\mathit{\boldsymbol{y}}}{{{r^3}}}\left[ {1 - {J_2}(\frac{{{R_e}}}{r})(7.5\frac{{{\mathit{\boldsymbol{z}}^2}}}{{{r^2}}} - 1.5)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mu _m}(\frac{{\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{y}}_m}}}{{r_{sm}^3}} + \frac{{{\mathit{\boldsymbol{y}}_m}}}{{r_m^3}}) + {\omega _{{v_y}}}\\ \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_z}}}{{{\rm{d}}t}} = - {\mu _e}\frac{\mathit{\boldsymbol{z}}}{{{r^3}}}\left[ {1 - {J_2}(\frac{{{R_e}}}{r})(7.5\frac{{{\mathit{\boldsymbol{z}}^2}}}{{{r^2}}} - 1.5)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mu _m}(\frac{{\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{z}}_m}}}{{r_{sm}^3}} + \frac{{{\mathit{\boldsymbol{z}}_m}}}{{r_m^3}}) + {\omega _{{v_z}}} \end{array} \right. $ | (3) |
式中,x、y、z、vx、vy、vz分别为月球探测器的3个位置矢量和3个速度矢量;μe、μm为地球和月球的引力常数;J2为地球引力二阶带谐项系数;xm、ym、zm是月球相对于地球的位置矢量;rm是月球相对于地球的矢径;rsm是探测器相对于月球的矢径;ωx、ωy、ωz、ωvx、ωvy、ωvz均为随机噪声。
为了简化计算,记T为采样间隔,状态方程则写为:
| $ {{\hat X}_k} = f({{\hat X}_{k - 1}}, k - 1) = {{\hat X}_{k - 1}} + {f_1}({{\hat X}_{k - 1}}){\rm{ \times }}\mathit{\boldsymbol{T}} $ | (4) |
式中,
由于系统结构并非线性,所以利用扩展卡尔曼滤波方法近似求解。首先对观测方程(1)(或其隐性公式(2))进行线性化处理,则可得到:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_k} = }\\ {\left( {\begin{array}{*{20}{c}} {\frac{{\partial {h_1}(X(t))}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial {h_1}(X(t))}}{{\partial \mathit{\boldsymbol{y}}}}}&{\frac{{\partial {h_1}(X(t))}}{{\partial \mathit{\boldsymbol{z}}}}}&0&0&0\\ {\frac{{\partial {h_2}(X(t))}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial {h_2}(X(t))}}{{\partial \mathit{\boldsymbol{y}}}}}&{\frac{{\partial {h_2}(X(t))}}{{\partial \mathit{\boldsymbol{z}}}}}&0&0&0\\ {\frac{{\partial {h_3}(X(t))}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial {h_3}(X(t))}}{{\partial \mathit{\boldsymbol{y}}}}}&{\frac{{\partial {h_3}(X(t))}}{{\partial \mathit{\boldsymbol{z}}}}}&0&0&0 \end{array}} \right)} \end{array} $ | (5) |
式中,
| $ {h_1}(X(t)) = \arccos (\frac{{\mathit{\boldsymbol{x}}{\rm{ \times }}{s_{1x}} + \mathit{\boldsymbol{y}}{\rm{ \times }}{s_{1y}} + \mathit{\boldsymbol{z}}{\rm{ \times }}{s_{1z}}}}{{\sqrt {{\mathit{\boldsymbol{x}}^2} + {\mathit{\boldsymbol{y}}^2} + {\mathit{\boldsymbol{z}}^2}} }}) $ | (6) |
则有
| $ \frac{{\partial {h_1}(X(t))}}{{\partial \mathit{\boldsymbol{x}}}} = \frac{{{s_{1x}}{r^2} - \mathit{\boldsymbol{x}}(\mathit{\boldsymbol{x}}{\rm{ \times }}{s_{1x}} + \mathit{\boldsymbol{y}}{\rm{ \times }}{s_{1y}} + \mathit{\boldsymbol{z}}{\rm{ \times }}{s_{1z}})}}{{{r^2}\sqrt {{r^2} - {{(\mathit{\boldsymbol{x}}{\rm{ \times }}{s_{1x}} + \mathit{\boldsymbol{y}}{\rm{ \times }}{s_{1y}} + \mathit{\boldsymbol{z}}{\rm{ \times }}{s_{1z}})}^2}} }} $ | (7) |
然后对状态方程(3)进行线性化处理得到:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}} = \mathit{\boldsymbol{I}} + \left( {\begin{array}{*{20}{c}} 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1\\ {\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&0&0&0\\ {\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&0&0&0\\ {\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&{\frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}}}&0&0&0 \end{array}} \right){\rm{ \times }}\mathit{\boldsymbol{T}} $ | (8) |
式中,I表示单位矩阵。
式(3)中,记
| $ J = 1 - {J_2}\left( {\frac{{{R_e}}}{r}} \right)(7.5\frac{{{\mathit{\boldsymbol{z}}^2}}}{{{r^2}}} - 1.5) $ | (9) |
可以得到:
| $ \frac{{\partial J}}{{\partial \mathit{\boldsymbol{x}}}} = 22.5\frac{{{J_2}{R_e}{\mathit{\boldsymbol{z}}^2}\mathit{\boldsymbol{x}}}}{{{r^5}}} - 1.5\frac{{{J_2}{R_e}\mathit{\boldsymbol{x}}}}{{{r^2}}} $ | (10) |
于是,有:
| $ \begin{array}{l} \frac{{\partial \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_x}}}{{{\rm{d}}t}}}}{{\partial \mathit{\boldsymbol{x}}}} = - {\mu _e}\frac{\mathit{\boldsymbol{x}}}{{{r^3}}}\frac{{\partial J}}{{\partial \mathit{\boldsymbol{x}}}} - {\mu _e}\frac{{{r^3} - 3{\mathit{\boldsymbol{x}}^2}}}{{{r^5}}}J - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\mu _m}\frac{{r_{sm}^2 - 3{{(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_m})}^2}}}{{r_{sm}^5}} \end{array} $ | (11) |
矩阵中其他结果同理可得。
将线性化后的观测方程和状态方程带入扩展卡尔曼滤波基本方程[10, 11]中,就可以在已知一个状态下月球探测器位置速度信息的情况下,利用星光角距观测值得到下一个状态下的月球探测器位置和速度信息的滤波结果。
2 仿真研究1) 初始数据模拟。通过STK软件模拟月球探测器在地月转移轨道上的运动轨迹,将模拟出的坐标和速度信息加入误差后得到星光角距观测值。
2) 滤波参数确定。系统状态噪声方差协方差矩阵为:
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {0.5}&0&0&0&0&0\\ 0&{0.5}&0&0&0&0\\ 0&0&{0.5}&0&0&0\\ 0&0&0&{0.05}&0&0\\ 0&0&0&0&{0.05}&0\\ 0&0&0&0&0&{0.05} \end{array}} \right] $ | (12) |
状态向量的误差协方差矩阵为:
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {1000}&0&0&0&0&0\\ 0&{1000}&0&0&0&0\\ 0&0&{1000}&0&0&0\\ 0&0&0&2&0&0\\ 0&0&0&0&2&0\\ 0&0&0&0&0&2 \end{array}} \right] $ | (13) |
观测量误差协方差矩阵为:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {10''}&0&0\\ 0&{10''}&0\\ 0&0&{10''} \end{array}} \right] $ | (14) |
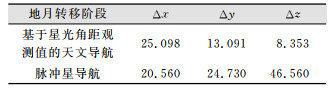
3) 仿真结果。图 2为仿真结果,采样间隔为10 s。由图 2可知,滤波后的x轴平均误差为25.098 km,最大误差为43.417 km;y轴的平均误差为13.091 km,最大误差为24.694 km;z轴的平均误差为8.353 km,最大误差为16.980 km。基于星光角距观测值的天文导航与脉冲星导航对比见表 1。
 |
| 图 2 仿真结果 Fig.2 Results of Simulation |
| 表 1 天文导航与脉冲星导航结果对比/km Tab.1 Results Compared with Pulsar Navigation/km |
 |
3 结束语
本文建立了基于星光角距观测值的自主天文导航模型,通过在地月转移轨道的仿真实验分析了这种模型的可行性。这种模型在月球探测器的地月转移轨道定位中,z方向上的精度要好于x方向和y方向,相对于脉冲星天文导航方法,在z轴精度上有了显著提高。同时发现星敏感器的精度会影响天文导航的精度,通过更复杂的积分方法也可以提高基于星光角距观测值的天文导航方法的精度。
| [1] |
宁晓琳, 房建成. 一种基于UPF的月球车自主天文导航方法[J]. 宇航学报, 2006, 27(4): 648-653. |
| [2] |
宁晓林, 房建成. 一种基于天体观测的月球车位置姿态确定方法[J]. 北京航空航天大学学报, 2006, 32(7): 756-759. |
| [3] |
Yenilmez L, Temeltas H. Autonomous Navigation for Planetary Exploration by a Mobile Robot[C]. 2003 International Conference on RAST, Istanbul, Turkey, 2003
|
| [4] |
Goldberg S B, Maimone M W, Matthies L.Stereo Vision and Rover Navigation Software for Planetary Exploration[C]. Aerospace Conference Proceedings, IEEE, Big Sky, MT, USA, 2002
|
| [5] |
刘林, 张巍. 月球探测器过渡轨道的短弧定轨方法[J]. 天文学报, 2007, 48(2): 220-227. |
| [6] |
李小军, 殷志祥, 蔡顺中. 月面探测器天文导航研究[J]. 测绘地理信息, 2015, 40(4): 26-28. |
| [7] |
刘建栋.天文导航技术在深空探测中应用新进展[C].中国天文学会年会, 北京, 2015
|
| [8] |
郗晓宁, 曾国强, 朱文耀. 从地面发射月球探测器的窗口选择[J]. 天文学报, 2000, 41(4): 361-372. |
| [9] |
李征航, 魏二虎, 王正涛, 等. 空间大地测量学[M]. 武汉: 武汉大学出版社, 2010.
|
| [10] |
周标准, 裴福俊, 董国成. 基于无迹卡尔曼滤波的月球车惯性/天文组合导航算法研究[J]. 科学技术与工程, 2012, 12(24): 6102-6106. |
| [11] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2015.
|
 2020, Vol. 45
2020, Vol. 45

